Apprentissage de la programmation informatique à la transition collège-lycée

Matthieu BRANTHÔME

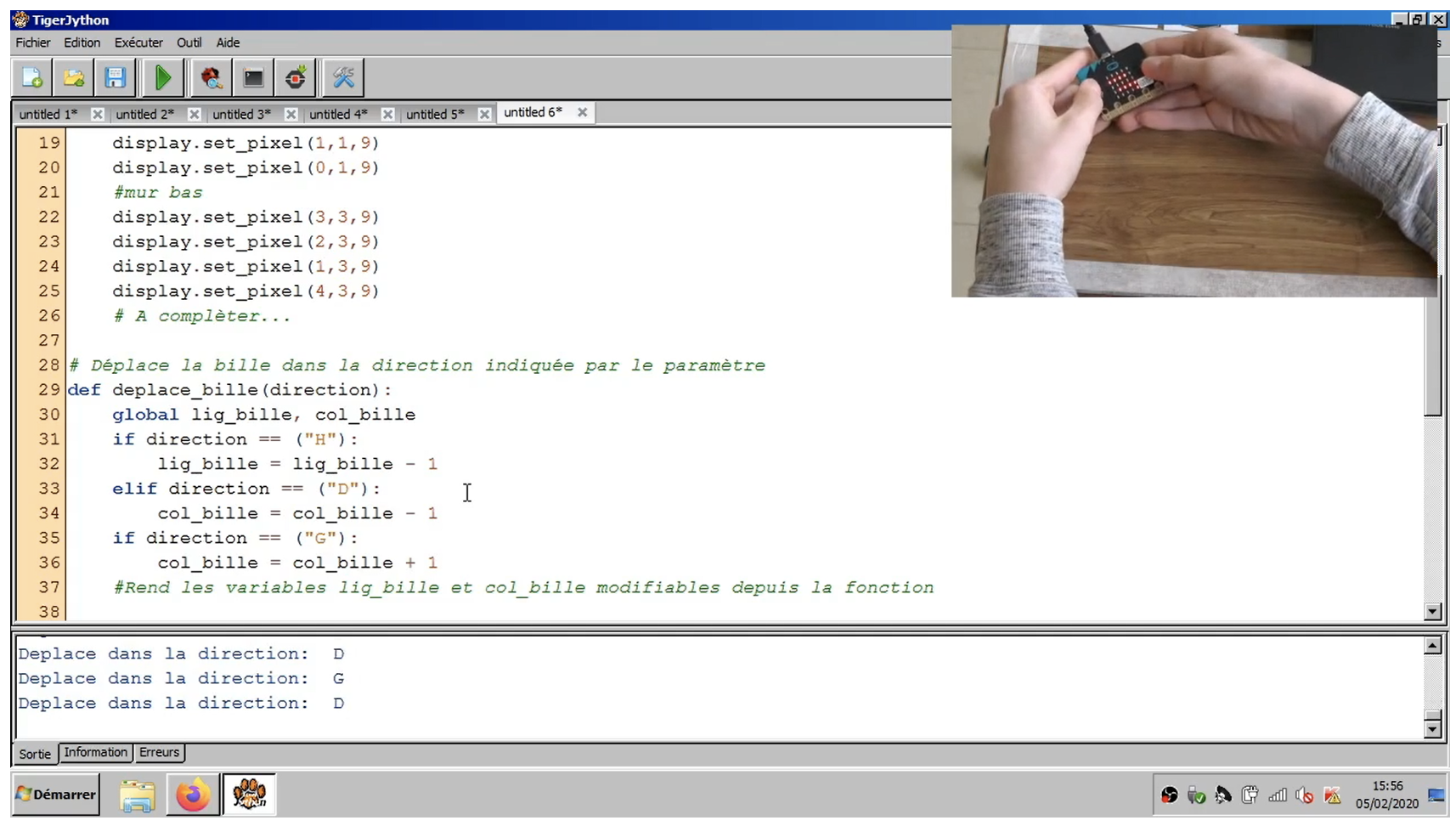
Dans un contexte sociétal dans lequel l’informatique et le « numérique » prennent une place toujours plus importante (Abiteboul et Dowek, 2017), les programmes scolaires français du primaire et du secondaire ont connu, ces dernières années, de fortes évolutions. Ainsi, au primaire et au collège, la programmation informatique fait désormais l’objet d’une initiation. Au lycée, de nouvelles matières dédiées ont vu le jour récemment : Sciences Numériques et Technologie (SNT) en seconde et Numérique et Sciences Informatiques (NSI) en première et terminale. L’université évolue également en proposant de nouveaux parcours permettant de former les enseignants dans ces nouvelles disciplines : création d’un nouveau CAPES et de masters MEEF associés.

Face à cet état de fait, nous pouvons faire deux constats. D’abord, nous faisons l’hypothèse d’une carence en ressources pédagogiques à destination des élèves et en contenus pour la formation des enseignants. Ensuite, sur le plan scientifique, les travaux portant sur l’informatique scolaire sont encore rares, notamment ceux mettant en œuvre des concepts théoriques de didactique (Caron et al., 2020), (Fluckiger, 2019).

Nous avons choisi, dans cet article, de nous focaliser sur un moment spécifique : la transition du collège au lycée, et plus particulièrement le passage de la programmation graphique par blocs au cycle 4 (logiciel Scratch) à la programmation, plus classique, en lignes de code en seconde (langage Python). Cette transition est susceptible d’engendrer des difficultés spécifiques que nous allons identifier puis chercher à comprendre dans l’objectif de proposer des moyens de les surmonter à travers la conception et la mise en œuvre d’une séquence d’enseignement dans une démarche d’ingénierie didactique.

Nous présentons d’abord une revue de travaux puis notre cadre théorique suivi de notre problématique et de notre méthodologie. Nous détaillons ensuite les résultats établis en suivant les étapes usuelles d’une ingénierie didactique : les analyses préalables, la conception et l’analyse a priori de la séquence qui en découle puis son analyse a posteriori. Enfin, nous concluons par quelques prolongements et ouvertures.

2. État de l’art

Le champ de recherche s’intéressant à l’enseignement-apprentissage de l’informatique en milieu scolaire est renaissant (Rogalski, 2015). En France, il se concentre principalement sur l’école primaire en portant son intérêt sur trois types de mises en œuvre (Baron et Drot-Delange, 2016) : la programmation graphique, la robotique pédagogique et l’informatique débranchée. Notons, tout de même, des travaux récents concernant le secondaire : Delmas-Rigoutsos propose une étude épistémologique de la notion de variable et formule des recommandations curriculaires permettant aux élèves de mieux appréhender cette notion (Delmas-Rigoutsos, 2020) ; Libert et Vanhoof ont conçu puis évalué des activités pour initier des élèves aux enjeux de la programmation concurrente et de la synchronisation (Libert et Vanhoof, 2020) ; Journault et al. proposent une séquence d’enseignement sous la forme d’activités débranchées autour de la notion de décidabilité algorithmique des problèmes (Journault et al., 2020). L’enseignement secondaire et plus particulièrement le lycée constituent ainsi un nouveau terrain pour les travaux sur l’informatique scolaire. Néanmoins, à notre connaissance aucune recherche ne s’est, jusqu’à présent, penchée sur la transition collège-lycée.

Envisageant, lors de notre expérimentation, l’utilisation d’un artefact programmable, nous avons mené une revue de travaux internationaux sur la programmation tangible. La programmation tangible (Physical Computing en anglais) est un concept défini par Przybylla et Romeike comme : « [It] covers the design and realization of interactive objects and installations and allows students to develop concrete, tangible products of the real world that arise from the learners’ imagination » (Przybylla et Romeike, 2014, p. 351). Elle fait l’objet de travaux dont l’arrière-plan théorique est celui du constructionnisme (Papert, 1980). Des articles transversaux (Blickstein, 2013), (Hodges et al., 2020), (Przybylla et Romeike, 2014) en présentent les vertus : elle améliore la créativité, l’engagement et la compréhension des apprenants, favorise la collaboration et ouvre l’informatique à un plus large public. Ces travaux proposent également une revue et une classification des nombreux matériels disponibles sur le marché : jouets programmables (ex : Bee-Bot), briques de construction programmables (ex : Lego Mindstorm), cartes avec microcontrôleurs (ex : Arduino) ou ordinateurs compacts (ex : Raspberry Pi). Il existe également de nombreuses études empiriques autour de la programmation tangible (Rubio et al., 2013), (Merkousis et al., 2017). Nous pouvons, en particulier, évoquer une très large expérimentation qui a été menée au Royaume-Uni en 2016 au cours de laquelle un million de cartes programmables BBC Micro:bit ont été distribuées gratuitement à tous les élèves de 11-12 ans. L’objectif gouvernemental était le développement massif de l’usage de la programmation et des technologies numériques. Plusieurs articles, proposent une évaluation du dispositif du côté des élèves (Sentance et al., 2017a) et des professeurs (Sentance et al., 2017b) après la première année de fonctionnement. Les résultats montrent que la carte Micro:bit favorise la créativité et que la nature physique du dispositif agit comme un facteur de motivation. Enfin, le caractère tangible de la carte est un élément clé qui stimule l’intérêt et améliore la compréhension des notions. Nous retenons donc pour la suite que la programmation tangible est susceptible d’améliorer : l’engagement dans les activités, la motivation et la compréhension des notions.

3. Cadre théorique

Nous exposons dans cette partie les concepts théoriques sur lesquels nous allons nous appuyer. Cette étude ayant pour but de concevoir puis de mettre en œuvre une expérimentation, elle s’inscrit dans la démarche méthodologique classique de l’ingénierie didactique s’appuyant sur la Théorie des Situations Didactiques (TSD) (Brousseau, 1998) dont nous exposons les principaux concepts. Nous définissons ensuite les notions qui nous permettront d’étudier les différences intrinsèques entre les langages Scratch et Python. Il s’agit des registres sémiotiques (Duval, 1993) et de quelques paradigmes et méthodes de programmation informatique.

3.1. Théorie des situations didactiques et ingénierie didactique

La TSD s’articule autour de deux notions centrales, celle de situation et celle de milieu didactique. Brousseau définit une situation comme : « une situation problème qui nécessite une adaptation, une réponse de l'élève. » (Brousseau, 1981, p. 112). Le milieu didactique est établi comme étant « constitué des objets (physique, culturels, sociaux, humains) avec lesquels le sujet interagit dans une situation [...] C’est le système antagoniste de l’actant [...] tout ce qui agit sur l’élève et ce sur quoi l’élève agit. » (Brousseau, 2010, p. 2).

Brousseau considère que les activités proposées aux élèves doivent tendre vers le modèle de la situation adidactique. Ce type de situation a pour objectif de provoquer chez l’élève des adaptations à travers le choix judicieux de problèmes par le professeur. Ces problèmes doivent permettre à l’élève d’agir de son propre mouvement, guidé uniquement par la logique interne de la situation, sans s’appuyer sur les intentions didactiques de l’enseignant qui se refuse à intervenir comme proposeur de la connaissance qu’il cible (Brousseau, 1998). Cet élève doit, de plus, pouvoir envisager une réponse initiale au problème posé sous la forme d’une procédure de base peu efficace s’appuyant sur ses connaissances antérieures qui n’est pas celle visée dans la situation. Ce savoir cible doit permettre, lorsqu’il est mis en œuvre, de passer de cette stratégie de base à une stratégie « optimale » (Bessot, 2003). Le « coût » des stratégies doit faire sens pour l’élève au regard des contraintes qui pèsent sur lui. Dans ces conditions, l’élève peut construire le savoir en jeu en lui octroyant véritablement du sens.

La TSD est le cadre privilégié sur lequel s’appuie la méthodologie de l’ingénierie didactique. Artigue en propose une définition opérationnelle en détaillant ses phases dans un découpage temporel que nous développons ci-dessous (Artigue, 1988).

D’abord, les analyses préalables. Il s’agit d’une étape préliminaire nécessitant l’évaluation des contenus épistémiques, des enseignements usuels et de leurs effets, des conceptions des élèves, des difficultés rencontrées et des diverses contraintes dans lesquelles va se situer l’expérimentation.

Ensuite, la conception d’une séquence et son analyse a priori. Lors de la conception de la séquence, le chercheur prend la décision d’agir sur un certain nombre de variables du système. Les variables globales fixent l’organisation générale de l’expérimentation et l’aménagement du milieu didactique. Les variables locales permettent la conception de la situation. L’analyse a priori permet ensuite de « déterminer en quoi les choix effectués permettent de contrôler les comportements des élèves et leur sens. » (Artigue, 1988, p. 258). Elle comporte donc deux aspects. Une partie descriptive qui consiste à : décrire et justifier les options choisies concernant la constitution et l’aménagement du milieu didactique ; motiver les choix de conception et expliciter les savoirs en jeu pour chaque situation. Suit une partie prédictive, il s’agit alors d’imaginer et d’anticiper les différentes stratégies de résolution possibles et vérifier que celles comportant le meilleur coût pour l’élève résultent bien de la mise en œuvre de la connaissance ciblée.

Vient ensuite l’expérimentation qui consiste en la mise en œuvre effective de la séquence conçue et au recueil de données empiriques.

Enfin, l’analyse a posteriori. C’est lors de cette dernière étape de mise en regard des faits avec les prédictions qu’a lieu la validation ou l’invalidation des hypothèses engagées dans la recherche. Il est ensuite possible de réitérer le processus, à l’aune des résultats obtenus.

3.2. Systèmes sémiotiques

La distinction entre un concept et ses représentations est un élément important pour la compréhension et la conceptualisation des objets théoriques. Duval qualifie ces productions de représentations sémiotiques et les décrit comme « des productions constituées par l’emploi de signes appartenant à un système de représentation qui a ses contraintes propres de signifiances et de fonctionnement. » (Duval, 1993, p. 39).

Un système de représentation peut constituer un registre sémiotique à la condition qu’il permette trois activités cognitives fondamentales : la formation d’une représentation identifiable comme une représentation dans un registre donné ; la transformation interne au registre ; la conversion, c'est à dire une transformation externe au registre de départ.

Duval constate un cloisonnement des registres sémiotiques chez les élèves qui ne reconnaissent pas les mêmes objets à travers des représentations exprimées dans des registres différents. Une des raisons de ce cloisonnement est l’hétérogénéité des différents registres qu’il mesure à leur degré de congruence. Les trois critères de congruence sont :

- la correspondance sémantique entre les différentes unités signifiantes de chaque représentation : à chaque unité signifiante d’une représentation, on peut associer un élément signifiant de l’autre ;

- l’univocité sémantique entre les représentations : à chaque unité signifiante de la représentation de départ doit correspondre une unique unité signifiante dans l’autre représentation ;

- l’organisation des unités signifiantes doit être la même : ces unités doivent être appréhendées dans le même ordre dans les deux présentations.

Nous analyserons donc, par la suite, à l’aide de ces concepts, le degré de congruence des différents registres sémiotiques manipulés par les élèves afin d’y déceler d’éventuelles sources de difficultés.

3.3. Paradigmes et méthodes de programmation

Les aspects multiples que peuvent prendre l’agencement des instructions dans un programme informatique se distinguent en différents paradigmes de programmation (Floyd, 1978). Nous nous limitons, dans le cadre de ce travail, à différencier deux des quatre paradigmes classiques : la programmation impérative et la programmation orientée objet.

Le paradigme de la programmation impérative est caractérisé par un état implicite de la mémoire, désigné par des variables. Cet état peut être modifié par des commandes (instructions) selon un principe de séquencement permettant un contrôle précis et déterministe des états (Hudak, 1989, p. 361). Ce paradigme de programmation s’attache donc à décrire comment les opérations doivent être effectuées séquentiellement pour résoudre un problème donné, en s’appuyant sur des espaces mémoires indexés par des variables.

Le paradigme de la programmation orientée objet consiste à concevoir et à manipuler uniquement des « objets » en tant qu’abstractions représentant des concepts où des entités du monde physique. Ces objets encapsulent en leur sein, à la fois les données (attributs) et les fonctionnalités qu’ils peuvent offrir (méthodes) (Stefik et Bobrow, 1985). Chaque type d’objet est défini, une fois pour toute, dans une « classe » qui spécifie ses attributs et décrit ses méthodes. Il peut, ensuite, être instancié, à l’exécution, en fournissant des valeurs particulières pour ses attributs. Son état peut, par la suite, être modifié par le seul accès à ses méthodes. En programmation orientée objet, pour traiter un problème, il s’agit donc de le modéliser à l’aide d’objets proposant diverses fonctionnalités, puis d’articuler les instanciations et les appels aux méthodes de ces différents objets pour fournir une solution.

Outre ces aspects paradigmatiques, d’autres paramètres peuvent influencer la façon de résoudre un problème à l’aide d’un ordinateur. Nous parlerons alors de méthodes de programmation. Certaines architectures matérielles et logicielles permettent l’exécution parallèle, c’est-à-dire en même temps, de pièces de code différentes. On parle alors de programmation parallèle ou concurrente. Il s’agit cependant de prendre certaines précautions relativement aux accès concurrents aux mêmes données. D’autres environnements autorisent, quant à eux, l’exécution d’un seul programme à la fois.

En ce qui concerne le déclenchement de l’exécution de ces pièces de code, elles peuvent être lancées en ligne de commande dans la console d’un ordinateur. Une alternative consiste à ce que ces programmes soient « en attente » d’évènements (appui sur une touche du clavier, mouvement de la souris, réception d’un message) pour s’exécuter. On parle alors de programmation évènementielle.

Nous mobiliserons, dans la suite, ces différents paradigmes et méthodes de programmation dans l’objectif de caractériser puis comparer les langages Scratch et Python.

4. Problématique

Nous partons de la question pratique suivante : comment accompagner et soutenir la transition du collège vers le lycée dans l’apprentissage de la programmation ?

- Quels sont les changements à l’œuvre lors de la transition collège-lycée ? Sont-ils susceptibles de causer des difficultés d’apprentissage ? Et si oui, quelles sont ces difficultés ?

- Quelle ingénierie didactique concevoir qui soit susceptible d’amoindrir ces potentielles difficultés ? Comment opèrent ces soutiens aux élèves.

5. Méthodologie

Lors de cette recherche, nous avons suivi la démarche méthodologique de l’ingénierie didactique dont nous avons présenté les grandes phases dans la section 3. Nous donnons ici les détails méthodologiques inhérents à chacune de ces phrases.

5.1. Analyses préalables

Lors des analyses préalables, nous nous sommes appuyés sur les instructions officielles du cycle 4 et de la classe de seconde (programmes de mathématiques et de SNT, documents d’accompagnements relatifs à l’algorithmique et à la programmation) ainsi que sur les propriétés intrinsèques des langages et des environnements techniques dans l’objectif d’analyser les changements sous-tendus par le passage de la programmation en Scratch à la programmation en Python.

5.2. Conception de la séquence

Pour cette phase, notre objectif était de concevoir une séquence d’enseignement à destination d’élèves en début de classe de seconde. Nous nous sommes d’abord reposés sur les éléments issus de notre revue de littérature et sur nos analyses préalables afin d’éclairer nos choix matériels et logiciels dans l’aménagement du milieu. Concernant la conception des activités proprement dites, nous avons construit une première version de notre séquence, de façon assez intuitive, en nous appuyant sur les savoirs ciblés. Nous avons ensuite l’analyse a priori des situations conçues, en repérant précisément les savoirs en jeu puis en anticipant toutes les stratégies répondant aux attendus. Ce travail a déclenché un cycle itératif d’analyses-modifications dont le produit final a été formalisé dans un support pédagogique numérique.

5.3. Expérimentation : terrain et données

Étant entré dans le dernier tiers de l’année scolaire nous n’avons pas eu accès à des élèves débutants de seconde, nous avons donc testé notre séquence auprès d’élèves de troisième. Cette expérimentation a pris la forme d’un atelier ayant eu lieu sur un temps extra-scolaire : un mercredi après-midi dans les locaux d’un collège rural de taille moyenne. Cela offrait l’avantage de disposer d’une large plage horaire permettant de mettre en œuvre notre séquence d’un seul tenant et de conclure l’atelier par un entretien-bilan collectif « à chaud ». Notre méthodologie nécessitant la mise en place d’un dispositif individuel assez lourd et engendrant un grand volume de données, nous avons limité le nombre de participants à six élèves. Ces élèves étaient volontaires et ont été recrutés suite à une rapide présentation de la carte Micro:bit à la fin d’un cours de mathématiques. Précisons que ces six volontaires ont un bon niveau scolaire en particulier en mathématiques. Il est également important de noter que, lors de cet atelier, nous avons joué le double rôle d’enseignant et de chercheur-observateur.

Pendant la première phase de l’expérimentation (trois heures) les élèves disposaient individuellement d’un ordinateur portable proposant un support pédagogique numérique, un environnement de développement ainsi que d’une carte Micro:bit. Notre dispositif de collecte de données, consistait, pour chacun des six élèves, à :

- enregistrer les activités à l’écran de son ordinateur au moyen du logiciel OBS Studio ;

- filmer ses interactions avec la carte programmable à l’aide d’une caméra fixe sur trépied située dernière lui ;

- enregistrer le son de la webcam de l’ordinateur afin de capturer ses interactions avec le professeur et les autres élèves.

La Figure 1, constituée de prises de vue effectuées juste avant et au cours de l’expérimentation, permet de se faire une idée de la mise en œuvre effective de ce dispositif.

Lors de la seconde phase, celle du bilan, nous avons réalisé un entretien collectif de type « focus-group » alors que tous les élèves s’étaient regroupés sur l’ilot central pour partager une collation. L’objectif de cet entretien était de recueillir les impressions et les commentaires des élèves concernant leur vécu au cours de cette expérimentation. Les questions ont été regroupées selon cinq thèmes : engagement et motivation ; connaissances préalables ; formes des activités et ressources d’appui ; difficultés rencontrées ; évaluation des apprentissages.

Le traitement des données ainsi recueillies a d’abord consisté en un travail technique. Pour chaque élève, il a fallu convertir, synchroniser puis fusionner les fichiers issus des différents dispositifs de captation. Nous avons ainsi réuni, sur un même support numérique toutes les interactions de l’élève avec le milieu didactique, c’est-à-dire : l’utilisation de l’environnement de développement, la consultation du support pédagogique, la manipulation de la carte programmable et les échanges avec le professeur. Nous proposons dans la Figure 2 une capture d’écran issue du montage vidéo final d’un élève. L’entretien a été retranscrit intégralement en gardant les thèmes dégagés lors de la rédaction du guide.

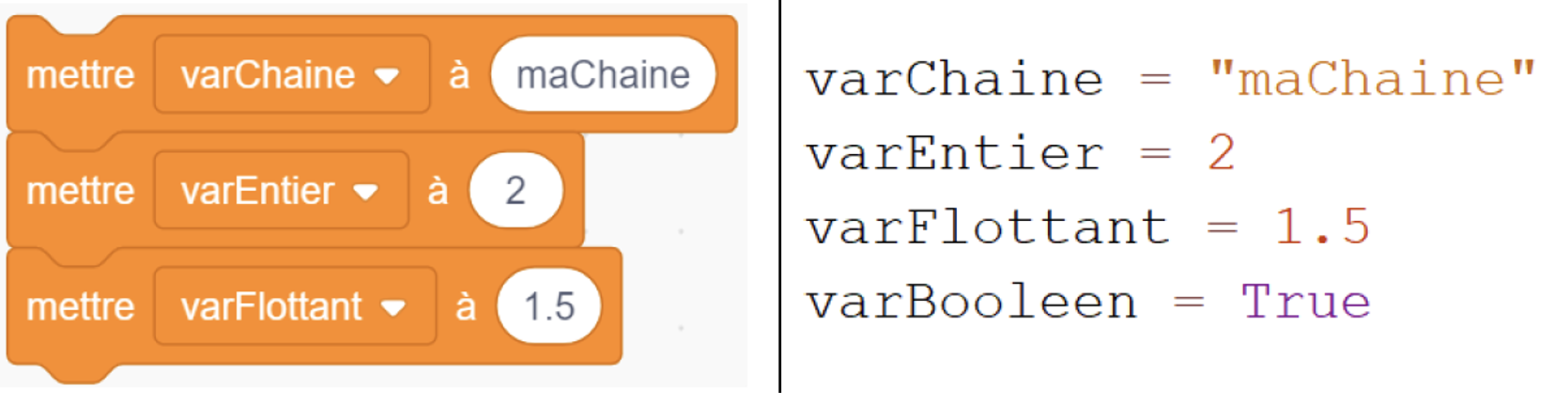
Nous avons ensuite procédé à une analyse qualitative de ces données qui a consisté à consigner et à retranscrire : toutes les interactions des élèves avec le milieu didactique, toutes les difficultés rencontrées ainsi que toutes les stratégies mises en œuvre par les élèves. Dans un second temps, nous avons procédé à la réduction quantitative du volume des données en entreprenant un comptage des différents éléments.

5.4. Analyses a posteriori

Notre analyse a posteriori s’appuie donc principalement sur ces éléments qualitatifs et quantitatifs issus de nos captations vidéo ainsi que sur la transcription de l’entretien. Nous avons essayé d’estimer en quoi notre proposition pouvait aider les élèves à surmonter les difficultés inhérentes à la transition Scratch-Python que nous avons décelées lors de nos analyses préalables. Nous présentons dans les sections suivantes les résultats que nous avons obtenus à chaque phase de l’ingénierie didactique.

6. Analyses préalables

Nous exposons dans cette section une analyse des différents changements sous-tendus par la transition collège-lycée dans l’apprentissage de la programmation, et en particulier le passage de la programmation en Scratch à la programmation en Python. Ces écarts ont été catégorisés dans quatre domaines que nous détaillons ci-après : les contenus épistémiques, les paradigmes et méthodes de programmation, les registres sémiotiques, et les types d’activités.

6.1. Contenus épistémiques

En consultant le programme et les documents d’accompagnement de mathématiques du cycle 4 (MEN, 2018), (MEN, 2016), nous pouvons affirmer qu’à ce niveau, les enseignants sont encouragés à adopter une approche très ludique à travers l’utilisation du logiciel Scratch qui est préconisé pour sa simplicité et sa robustesse. Les concepts à étudier sont principalement : les notions d’algorithme et de programme, la notion de variable, les boucles et la structure conditionnelle.

La lecture des programmes et des documents d’accompagnement de mathématiques (MEN, 2017), (MEN, 2019b), (MEN, 2019a) et de SNT (MEN, 2019c) de seconde, indique que, pour cette classe, les objectifs en termes de savoirs sont d’approfondir les notions introduites au cycle 4 (variables, structure conditionnelle et boucles), tout en ajoutant trois nouveautés : le typage des variables, la notion de fonction et la production d’un programme sous forme textuelle. Concernant les activités, il est clairement précisé qu’elles doivent être au service des autres parties du programme. Un langage de programmation est préconisé sans détour : il s’agit de Python. Il a été choisi pour sa simplicité et sa popularité (large écosystème dans la sphère éducative).

Au-delà des contenus épistémiques prescrits par l’institution à travers ses documents officiels, la programmation en Python conduit les apprenants à se confronter à une série de nouveaux savoirs de nature technique. En effet, l'environnement Scratch permet de se concentrer uniquement sur la partie algorithmique en proposant une programmation de très haut niveau cachant toute la partie technique liée à la machine. Les blocs opèrent un contrôle syntaxique total et sémantique partiel par leurs formes et couleurs. Les programmes se lancent par déclenchements sur des évènements, les sorties se font par l’expression ou les actions des « lutins ».

Le langage Python n’a pas été conçu dans un but pédagogique. Son utilisation nécessite l’installation d’un éditeur de code et d’un interpréteur. Selon l’environnement de développement choisi, il peut être nécessaire d’enregistrer le code source du programme dans l’arborescence du système de fichier de l’ordinateur puis de lancer l’interprétation du programme à travers la saisie d’une ligne de commande dans la console système de l’ordinateur. Dans le cadre de l’apprentissage du langage Python, il devient donc nécessaire pour les apprenants d’acquérir des connaissances, même partielles et imprécises, à propos de l’architecture des machines et des systèmes d’exploitations. De nouvelles contraintes apparaissent également : la nécessité de correction syntaxique et sémantique du texte du programme, le blocage en cas d’erreur, la gestion dans la console système des entrées-sorties permettant les interactions avec le programme. Tout ceci constitue, de fait, un ensemble de nouveaux savoirs techniques qui pourraient parasiter l’apprentissage de ceux prescrits par l’institution. En effet, le risque encouru par les élèves au cours de cette exposition abondante et soudaine à de nouveaux éléments est la survenue d’une surcharge cognitive (Sweller, 1988) potentiellement néfaste à l’appréhension des concepts algorithmiques visés par les programmes d’enseignements.

6.2. Paradigmes et méthodes de programmation

Le passage du logiciel Scratch à la programmation en Python opère un basculement dans le paradigme et la méthode de programmation. En effet, le logiciel Scratch permet une programmation orientée objet. Le code est porté par des objets : les « lutins » et agit en modifiant leurs attributs (position, apparence, sons ou messages émis). Chaque programme, nécessairement attaché à un de ces objets peut donc être considéré comme l’une de ses méthodes. Le langage Python est utilisé en classe de seconde de manière impérative, c’est-à-dire en exécutant une suite séquentielle d'instructions modifiant les valeurs de variables. Il s’avère que les changements de paradigmes de programmation peuvent représenter des obstacles lors des apprentissages car ils nécessitent des adaptations cognitives de la part des apprenants (Khazaei et Jackson, 2002), (White et Sivitanides, 2005).

D’autre part, le logiciel Scratch met en œuvre les méthodes de programmation parallèle et évènementielle. Ainsi, l’exécution du code est déclenchée par des évènements : clic sur une zone, touche appuyée, message reçu, etc. Cela peut, par ailleurs, occasionner l’exécution concurrente de plusieurs pièces de code. En Python, en fonction de l’environnement de développement utilisé, le code est lancé à l’intention du programmeur, en ligne de commande, ou au mieux, en cliquant sur un bouton de l’environnement de développement. De surcroît, la programmation parallèle n’est pas envisageable de façon simple au niveau du lycée. Il apparait que ces différences modifient la façon dont on peut envisager la réponse à un problème posé. Les élèves doivent s’exprimer différemment en langage Python, en s'adaptant à une palette de possibilités plus pauvre. L’expression se retrouve, d’une certaine manière, bridée par le carcan de la séquentialité, alors que les élèves ont pris l’habitude au collège avec Scratch, d’utiliser la programmation évènementielle et parallèle.

6.3. Registres sémiotiques

La programmation en Scratch et la programmation en Python font appel à des registres sémiotiques bien différents pour implémenter les concepts algorithmiques. Nous les nommerons, dans la suite, respectivement registre des blocs et registre des instructions.

Le registre des blocs est constitué de représentations sémiotiques sous la forme de blocs manipulables et assemblables de différentes formes et couleurs. Les couleurs définissent neuf catégories d’usages (orange : contrôle, violet : apparence, vert : opérateur, etc.) et les formes précisent à la fois l’organisation et la structure du programme (bloc de début, bloc de fin, bloc d’empilement, bloc d’imbrication), elles peuvent aussi indiquer le type du bloc (hexagonale : booléen ; rectangulaire arrondie : nombre ou chaîne de caractères).

Le registre des instructions comprend des représentations sémiotiques sous forme textuelle. Il s’agit des mots réservés du langage Python. Ce sont des mots-clés en anglais prenant la forme de prépositions (« for », « in ») de conjonctions (« while », « if », « else ») ou de verbes à l’impératif (« return », « print ») mélangés avec des symboles mathématiques (« = », « > ») ou typographiques (« : », « ( », « " »).

Pour chaque notion algorithmique issue des programmes (variable, conditionnelle, boucle bornée et non-bornée, fonction), nous avons reproduit les représentations sémiotiques dans le registre des blocs et des instructions puis nous avons évalué, à l’aune des critères énoncés par Duval, leur degré de congruence (faible, moyen ou fort). Rappelons que ces critères de congruence sont : la correspondance sémantique, l’univocité sémantique et l’organisation des unités signifiantes.

Variable : congruence moyenne. En observant les deux représentations sémiotiques reproduites dans la Figure 3, on retrouve une correspondance sémantique entre différentes unités signifiantes, à l’exception des guillemets caractérisant les chaînes de caractères en Python non-présents dans le registre des blocs. L’univocité sémantique n’est cependant pas totalement respectée car deux éléments « mettre » et « à » correspondent au signe « = » en Scratch. L’organisation des unités signifiantes est globalement la même.

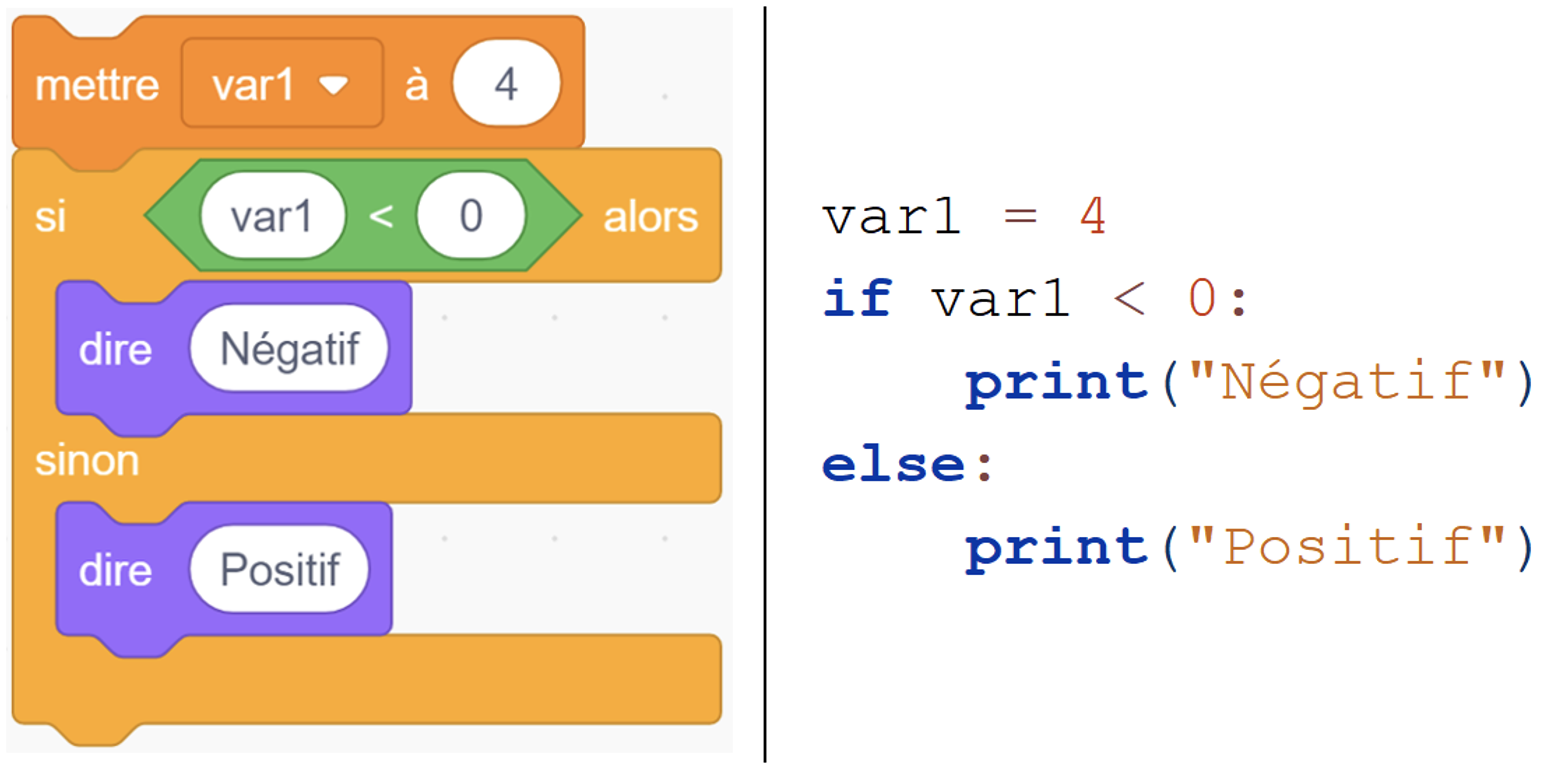
Conditionnelle : congruence forte / moyenne. On peut affirmer, après l’étude de la Figure 4, que la congruence est très forte entre les deux représentations. La correspondance sémantique est quasi-parfaite, mis à part les « : » suivant le « else » qui n’ont pas de pendant dans le registre des blocs. L’organisation et l’ordre étant elles aussi respectées. En revanche, si le nombre de branches de la conditionnelle est supérieur à deux, on perd l’univocité sémantique car il faut imbriquer plusieurs blocs Scratch « si-sinon » pour produire l’équivalent du « elif » en Python.

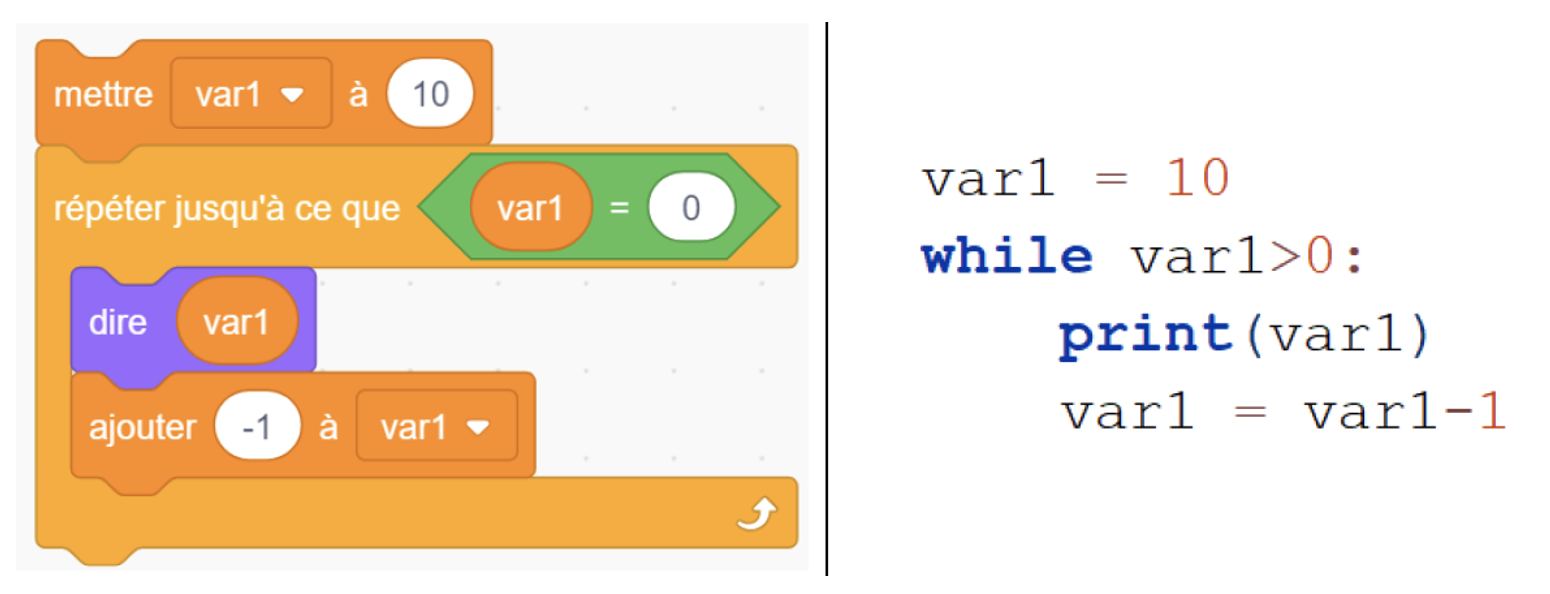
Boucle bornée : congruence faible. L’examen de la Figure 5 indique qu’il n’y a quasiment aucune correspondance sémantique entre les différentes unités signifiantes des deux représentations. Seul le « 10 » correspond. Remarque : Il n’y a pas de variable de boucle incrémentée automatiquement dans Scratch.

Boucle non-bornée : congruence faible. En observant la Figure 6, nous pouvons affirmer qu’il n’y pas de correspondance sémantique entre les unités signifiantes. La condition d’arrêt étant inversée dans Scratch : « jusqu’à ce que » contre « while » (tant que) en Python.

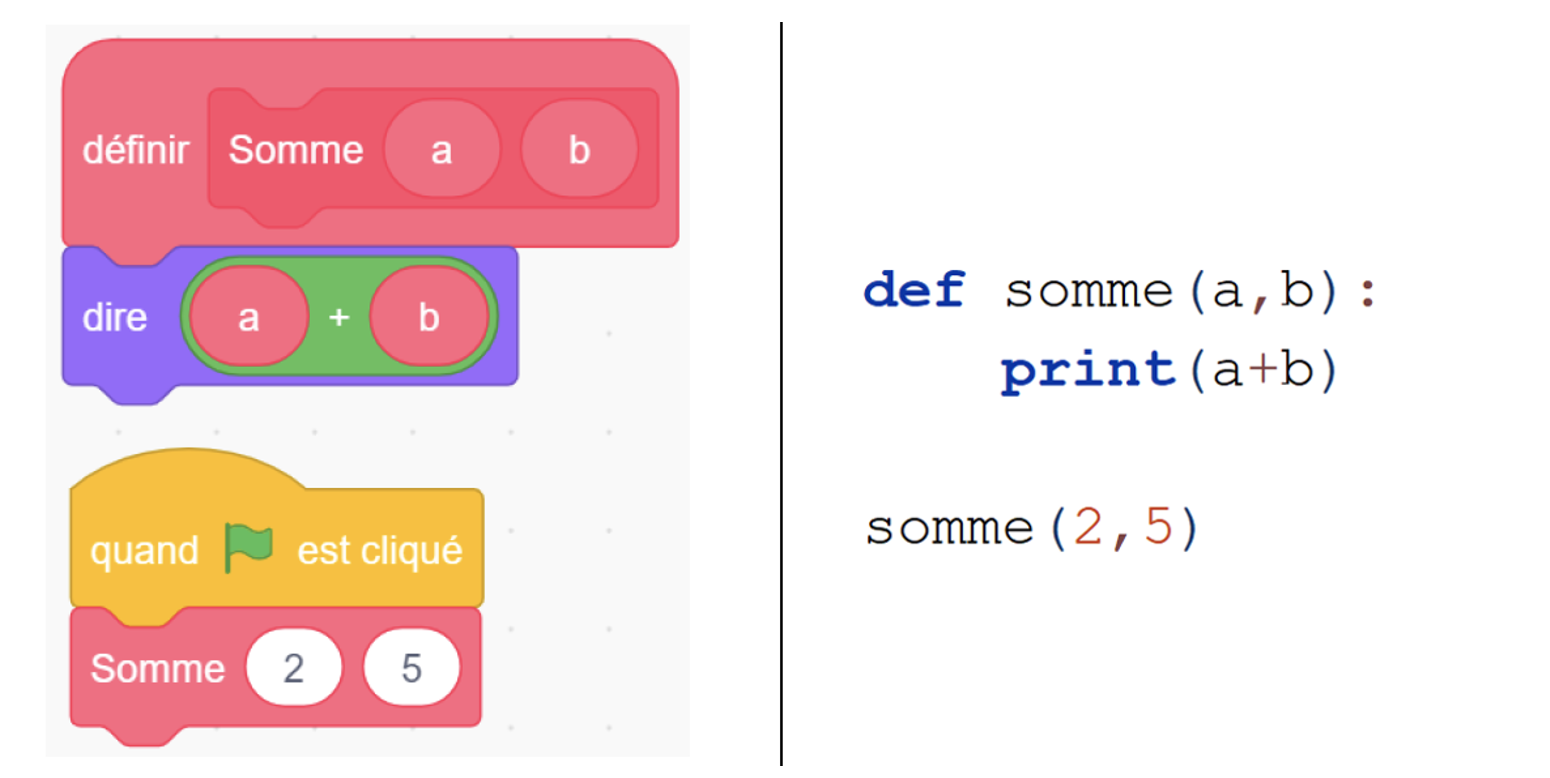
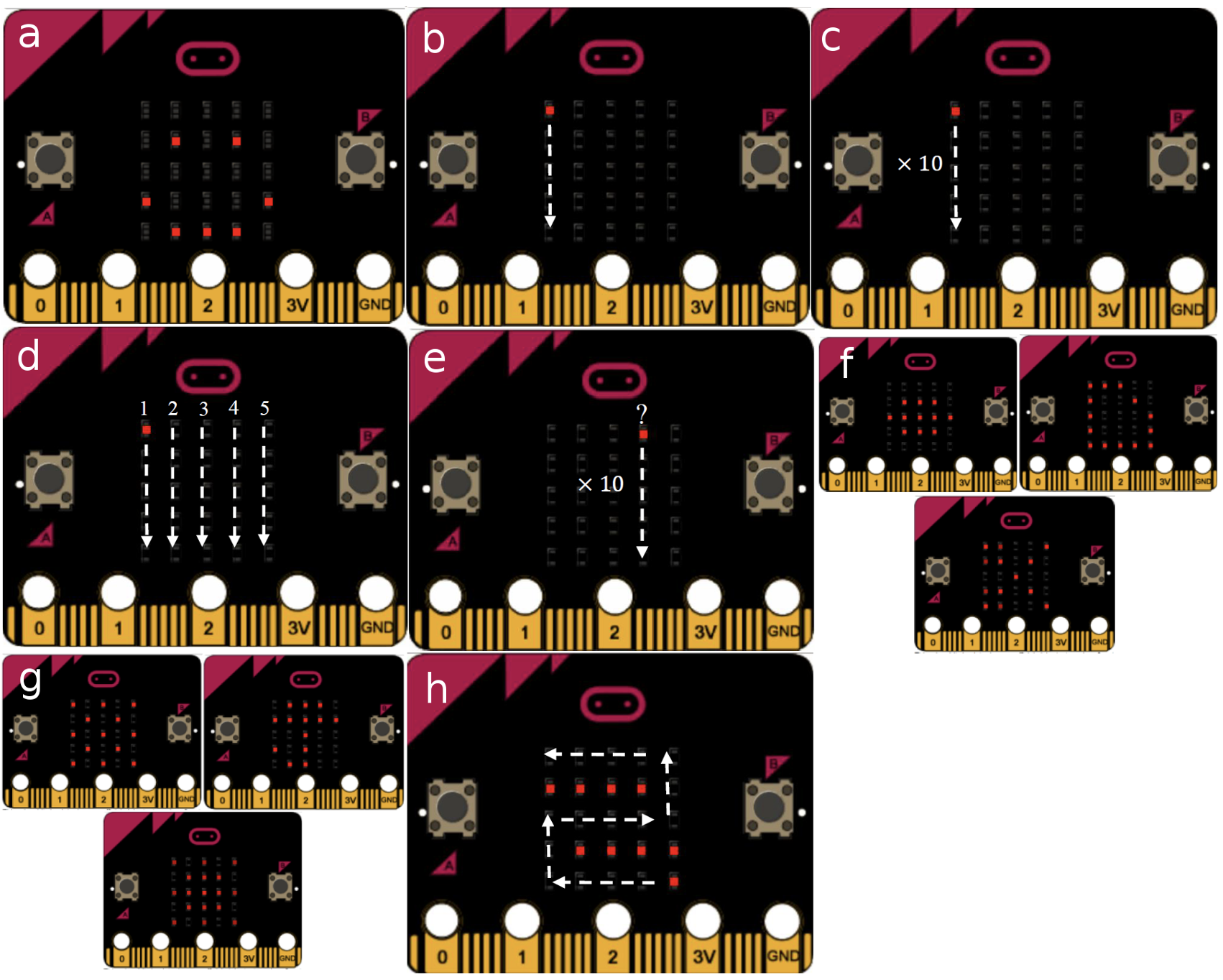
Fonction : congruence forte / moyenne. Après observation de la Figure 7, nous pouvons avancer que le degré de congruence est très élevé pour les fonctions sans retour, car tous les critères sont respectés : correspondance sémantique, univocité sémantique et organisation des unités signifiantes. En revanche, si la fonction retourne une valeur, il n’est pas possible de l’implémenter en l’état dans Scratch. Il faudra pour cela passer par la modification d’une variable globale ou une sortie (« dire »), ce qui diminue grandement le degré de congruence, car l’unité signifiante « return » ne correspond à rien dans Scratch.

Pour résumer, nous pouvons dire que le degré de congruence est assez disparate d’un concept à l’autre. Les variables, les conditionnelles et les fonctions permettent un changement de registre assez immédiat, là où les boucles ont des représentations assez éloignées dans les deux registres. Ces ressemblances et différences ont sans doute une influence sur l’apprentissage de la programmation en Python par les élèves. En effet, ils ont déjà rencontré certains concepts en cycle 4 dans leur représentation dans le registre des blocs. De tels connaissances antérieures peuvent constituer une aide pour les notions de variables, de conditionnelles et de fonctions (notons que, bien que disponibles dans Scratch, les fonctions ne font pas partie des attendus du collège) et plutôt un obstacle pour l’appréhension des notions de boucles (bornées et non bornées) en Python.

6.4. Type d’activité

Au cycle 4, les enseignants sont incités à proposer à leurs élèves des activités dans le registre ludique, en témoigne cet extrait du programme de mathématiques : « Les élèves s’initient à la programmation, en développant dans une démarche de projet [...] Exemples d’activités possibles : jeux dans un labyrinthe, jeu de Pong, bataille navale, jeu de Nim, Tic-Tac-Toe, jeu du cadavre exquis. » (MEN, 2018, p. 40). En revanche, les programmes d’enseignement de seconde invitent les enseignants à quitter le domaine ludique pour proposer aux élèves des activités en lien avec les autres parties des programmes : « À la différence du programme de mathématiques du cycle 4 du collège, il s’agit donc d’adosser explicitement les activités de la partie algorithmique et programmation aux mathématiques. » (MEN, 2017, p. 1). Pour illustrer, nous pouvons citer quelques exemples. Nous trouvons dans le programme de mathématiques (MEN, 2019b) parmi les activités de programmation : « Déterminer si un entier naturel �� est multiple d’un entier naturel �� » ; « Déterminer une équation de droite passant par deux points donnés ». Le programme de SNT (MEN, 2019c) propose lui aussi des activités en lien avec le reste du programme, citons par exemple : « Calculer la popularité d’une page à l’aide d’un graphe simple puis programmer l’algorithme ».

Au regard de l’âge des élèves de seconde et de leurs centres d'intérêt, il est possible que ce type d'activités, moins ludiques et plus scolaires, entraîne une diminution de leur engagement affectif (Hannula et al., 2019) dans les travaux proposés. Ceci peut donc constituer un obstacle dans la transition collège-lycée.

7. Conception de la séquence

Nous exposons dans cette section les choix qui ont gouverné la conception de notre séquence d’enseignement.

7.1. Variables globales : aménagement du milieu

La séquence que nous avons conçue prend la forme d’un atelier, d’une durée de trois heures, destiné à des élèves en début de classe de seconde. Au cours de cette activité, nous mettons à la disposition des élèves, différents éléments : un dispositif programmable, une liste de défis, un environnement de développement et un support pédagogique numérique. Nous détaillons ces éléments ci-dessous.

7.1.1. Une carte programmable BBC Micro:bit

Il s’agit ici de programmer un dispositif électronique pédagogique : la carte BBC Micro:bit. Nous avons fait le choix d’un tel matériel dans l’objectif d’accroitre l’engagement des élèves dans les activités (voir résultats de recherche en section 2). Cette carte est programmable en Python par l’intermédiaire d’une liaison USB. Elle dispose, entre autres, d’un écran constitué d’une matrice de 25 LED, de deux boutons utilisateurs et d’un capteur de luminosité.

7.1.2. Un ensemble de défis à relever

Nous avons conçu les activités sous la forme de défis à relever dans une volonté de ludification avec l’objectif d’encore renforcer l’implication des élèves (Dicheva et al., 2015). Il s’agit, dans un souci de difficultés croissantes, de commencer par des affichages basiques sur la matrice de LED de la carte et de proposer ensuite la mise en œuvre de jeux simples. La résolution progressive, et dans l’ordre, de ces situations permet de gagner des « badges numériques » de développeur Python. Nous en avons créé trois, représentant trois niveaux : débutant, confirmé et expert. Ils permettent de valider, par étapes, les réussites des élèves. Le but est, ici aussi, de favoriser l’investissement des élèves dans les activités (Abramovich et al., 2013), (Gibson et al., 2015). Ces badges sont des images numériques simples, ils ne respectent pas les formats standards partageables en ligne. Pour pallier à ce manque, nous avons décidé de les imprimer et de les plastifier afin de pouvoir les distribuer physiquement aux élèves au fur et à mesure de leurs succès.

7.1.3. Un EDI proposant des aides

L’environnement de développement que nous avons choisi est un Environnement de Développement Intégré (EDI), c’est à dire un logiciel permettant à la fois l’édition du code et la gestion des interactions avec l’interpréteur Python (lancement des programmes, gestion des entrées-sorties, récupération des erreurs). Il s’agit du logiciel « TigerJython » issu des travaux du chercheur suisse Tobias Kohn. Au cours de sa thèse (Kohn, 2017), il a étudié les erreurs les plus courantes d’étudiants novices en programmation Python pour ensuite développer un EDI offrant des fonctionnalités de localisation et d’explications de ces erreurs courantes. Les messages sont affichés in situ et formulés en français dans un registre pratique et compréhensible par des débutants. Ce que ne permettent pas les EDI Python traditionnels qui se contentent, en général, d’afficher dans la console les erreurs détectées par l’interpréteur (messages en anglais et de nature plus technique). « TigerJython » offre également la possibilité de s’interfacer facilement avec la carte BBC Micro:bit (un bouton permet, en un clic : la vérification syntaxique précoce, l’enregistrement, le téléversement et le lancement du programme depuis la carte). Les erreurs non levées par l’EDI sont classiquement détectées par l’interpréteur de la carte puis sont remontées dans la console de l’EDI.

7.1.4. Un support pédagogique numérique riche

Le support pédagogique de notre séquence se présente sous la forme d’une page Web. Nous avons opté pour un média numérique car cela permet : de proposer des contenus plus riches et attractifs comme des animations ; d’offrir une meilleure agilité en facilitant la navigation entre les différentes parties à l’aide de liens hypertextes et d’un menu fixe sur la gauche de l’écran ; de favoriser les copier-coller et, par là même, d’éviter au maximum les erreurs syntaxiques ; de pouvoir profiter des fonctionnalités de recherche dans une page qu’offrent les navigateurs.

Ce support pédagogique est consultable en ligne (Branthôme, 2020). Il contient, dans l’ordre d’apparition, les éléments suivants.

Un guide de démarrage reprenant les grands principes de la programmation textuelle et les procédures de base permettant l’utilisation de l’environnement de développement.

Un mémo récapitulant les principaux concepts de programmation que l’on peut mettre en œuvre à l’aide du langage Python. Nous en avons distingué cinq : les variables, les conditionnelles, les boucles bornées, les boucles non-bornées et les fonctions. Nous y présentons chaque concept à travers un court texte, suivi de sa structure générique et d’un exemple illustratif.

Une liste des 6 défis (certains comportant plusieurs actions) à relever. Pour chaque action, un texte sommaire décrit le fonctionnement attendu. Il est important de préciser que nous avons pris soin, dans cette formulation, de ne pas laisser transparaître les concepts et savoirs en jeu dans la situation dans le but de préserver au maximum leur adidacticité. Les défis sont, en majorité, illustrés d’une photo ou d’une animation permettant de lever toute ambiguïté concernant les attendus.

Enfin, il est important d’évoquer les fonctions du professeur dans cet atelier. Son rôle est de présenter succinctement le matériel aux élèves en début d’atelier puis de se mettre à leur disposition pour les aider à résoudre, en cas de nécessité, les problèmes qu’ils rencontrent. Les situations ayant été conçues en suivant le modèle adidactique, les élèves doivent cependant être autonomes vis-à-vis des savoirs en jeu, c’est à eux de trouver quels concepts, détaillés dans le mémo, doivent être mis en œuvre pour relever les défis et les actions. Nous venons de décrire les choix que nous avons faits au sujet des variables globales, nous allons maintenant entrer dans le détail des variables locales.

7.2. Variables locales : conceptions des activités

Rappelons au préalable que, sur le modèle des situations adidactiques, les savoirs en jeu ne sont pas explicités dans les situations proposées mais sont rendus nécessaires par leur logique interne. Le Tableau 1 reprend une partie des résultats de notre analyse a priori. Pour chaque défi et chaque action, nous exposons : une brève description de la situation (illustrée dans la Figure 8), les fonctions à disposition des élèves pour interagir avec la carte, les notions en jeu en lien avec le programme ainsi que leur caractère obligatoire (O) ou facultative (F) dans la résolution du problème.

Description défis / actions	Fonctions à disposition	Notions en jeu
Défi 1 : afficher un smiley sur l’écran de la carte (Figure 8-a).	* set_pixel(x,y,i) - allume la LED à l’adresse x,y avec l’intensité i.	D1N1 : utilis. fonction - avec arg. sans retour. (O)
Défi 2 : simuler une pluie aléatoire à l’écran. Action 1 : faire tomber une goutte dans la 1ère colonne (Figure 8-b).	* set_pixel(x,y,i) * sleep(t) – met en pause l’exécution pendant t millisecondes.	D2A1N1 : utilis. fonction - avec arg. sans retour. (O)
Défi 2 / Action 2 : faire tomber dix gouttes de suite dans la 1ère colonne (Figure 8-c).	* set_pixel(x,y,i) * sleep(t)	D2A2N1 : utilis. fonction - avec arg. sans retour. (O) D2A2N2 : boucle bornée - sans variable de boucle. (F)
Défi 2 / Action 3 : faire tomber une goutte une fois dans chaque colonne (Figure 8-d).	* set_pixel(x,y,i) * sleep(t)	D2A3N1 : utilis. fonction - avec arg. sans retour. (O) D2A3N2 : boucle bornée - avec variable de boucle. (F)
Défi 2 / Action 4 : faire tomber dix fois une goutte de pluie dans une colonne à chaque fois choisie aléatoirement (Figure 8-e).	* set_pixel(x,y,i) * sleep(t) * randint(x,y) – retourne un entier aléatoire entre x et y.	D2A4N1 : utilis. fonction - avec arg. sans retour. (O) D2A4N2 : utilis. fonction - avec arg. avec retour. (O) D2A4N3 : affect. et utilisation d’une variable. (O) D2A4N4 : boucle bornée - sans variable de boucle. (F)
Défi 3 : jeu Pierre-feuille-ciseaux. Afficher de façon aléatoire à l’écran : une pierre, une feuille ou des ciseaux (Figure 8-f).	* show(image) – affiche des images prédéfinies à l’écran de la carte. * randint(x,y)	D3N1 : utilis. fonction - avec arg. sans retour. (O) D3N2 : utilis. fonction - avec arg. avec retour. (O) D3N3 : affect. et utilisation d’une variable. (O) D3N4 : conditionnelle - branche « if ». (O) D3N5 : conditionnelle - branche « elif ». (F) D3N6 : conditionnelle - branche « else ». (F)
Déf 4 : jeu de rapidité. Le but du jeu est de réussir à appuyer plus de 30 fois sur le bouton A de la carte en 5 secondes. Tant que ce nombre n’est pas atteint, le jeu recommence.	* scroll(mess) – affiche un message sur l’écran de la carte. * sleep(t) * ba.get_presses() – retourne le nombre d’appuis sur le bouton A	D4N1 : utilis. fonction - avec arg. sans retour. (O) D4N2 : utilis. fonction - sans arg. avec retour. (O) D4N3 : affect. et utilisation d’une variable. (O) D4N4 : boucle non-bornée. (O) D4N5 : expression d’une chaîne de caractères. (O)
Défi 5 : station météo. Afficher à l’écran une image en fonction de la luminosité ambiante. Entre 0 et 10 : nuit étoilé ; entre 10 et 150 : un parapluie ; entre 150 et 255 : un soleil (Figure 8-g).	* show(im) * print(val) - permet de tracer les valeurs de luminosité dans la console. *read_light_level() – renvoie le niveau de luminosité (0-255) qui arrive sur l’écran.	D5N1 : utilis. fonction - avec arg. sans retour. (O) D5N2 : utilis. fonction - sans arg. avec retour. (O) D5N3 : affect. et utilisation d’une variable. (O) D5N4 : conditionnelle - branche « if ». (O) D5N5 : conditionnelle - branche « elif ». (O) D5N6 : conditionnelle - branche « else ». (F)
Défi 6 : programmer un labyrinthe parcourable à l’aide d’une « bille » dirigeable par les boutons de la carte (Figure 8-h). Action 1 : Compléter la fonction dessine_mur() qui dessine le labyrinthe.	* set_pixel(x,y,i)	D6A1N1 : utilis. fonction - avec arg. sans retour. (O) D6A1N2 : déf. fonction - sans arg. sans retour. (O)
Défi 6 / Action 2 : Compléter la fonction depl_bille(dir) qui déplace la « bille » en fonction de la chaine de caractères qu’elle prend en entrée. (« H », « G » ou « D »)	* set_pixel(x,y,i)	D6A2N1 : utilis. fonction - avec arg. sans retour. (O) D6A2N2 : déf. fonction - avec arg. sans retour. (O) D6A2N3 : affect. et utilisation d’une variable. (O) D6A2N4 : conditionnelle - branche « if ». (O) D6A2N5 : conditionnelle - branche « elif ». (F) D6A2N6 : comparaison de chaînes de caractères. (O)

8. Analyses a posteriori

En nous appuyant sur les données récoltées lors de l’expérimentation, nous avons déterminé, dans chaque domaine, si les activités proposées ont permis de réduire les contraintes que nous avons repérées lors de l’analyse préalable.

8.1. Contenus épistémiques : apprentissages et réduction des contraintes techniques

Nous avons, en premier lieu, évalué les apprentissages des élèves dans les notions du cycle 4 à consolider (variable, conditionnelle, boucles bornées et non-bornées) et dans celles à introduire en seconde (fonctions et typage). Pour cette analyse, nous nous sommes basés sur l’analyse a priori des défis et sur les stratégies utilisées par les élèves.

Nous pouvons distinguer deux cas, d’abord, certaines notions pouvaient être implémentées de façon facultative. Autrement dit, le problème pouvait être résolu sans les convoquer, leurs utilisations permettant cependant de fournir une solution optimale. Nous considérons dans ce cas, à la suite de Brousseau, que si l’élève a réussi à mettre en œuvre la notion en jeu de manière autonome (en se saisissant des éléments présents dans le milieu didactique, sans l’aide explicite du professeur), c’est qu’il a pu acquérir des connaissances relatives à cette notion en lui assignant du sens. Dans le Tableau 2, nous avons compilé pour chaque notion facultative contextualisée dans un défi : le nombre d’élèves ayant réussi le défi de manière autonome parmi les élèves l’ayant tenté ; le nombre d’élèves ayant implémenté cette notion parmi ceux ayant réussi le défi. Par exemple, pour la dernière ligne : la branche conditionnelle « else » était facultative dans le défi 5, ce défi a été réussi en autonomie par quatre élèves parmi les cinq l’ayant tenté, et un seul parmi eux a implémenté la branche conditionnelle « else ».

Notions contextualisées	Réussites défi	Implément.
D2A2N2 : boucle bornée.	5/6	5/5
D2A4N4 : boucle bornée.	6/6	6/6
D2A3N2 : boucle bornée + var boucle.	4/6	3/4
D3N5 : branche conditionnelle « elif ».	5/6	4/5
D6A2N5 : branche conditionnelle « elif ».	2/3	2/2
D3N6 : branche conditionnelle « else ».	5/6	1/5
D5N6 : branche conditionnelle « else ».	4/5	1/4

Nous pouvons remarquer que les boucles bornées, bien que non nécessaires, ont été quasi systématiquement utilisées lorsque le défi est réussi en autonomie (D2A2N2, D2A4N4, D2A3N2 : 14/15 - 93%). Nous pouvons donc avancer que les élèves ont majoritairement intégré cette notion en lui attachant du sens quant à la répétition du code. En effet les stratégies mettant en œuvre cette boucle étaient optimales relativement à la longueur des programmes. La branche conditionnelle « elif » a été mise en œuvre pratiquement à chaque fois qu’elle pouvait l’être (D3N5, D6A2N5 : 6/7 – 86%), ce qui n’est pas le cas de la branche « else » (D3N6, D5N6 : 2/9 – 22%). Nous pouvons proposer une explication qui découle de l’observation de l’activité des élèves lors du défi 3 (première exposition à la conditionnelle). Ainsi, lors de ce défi, les élèves se sont tous appuyés sur l’exemple proposé dans le mémo sous la forme « if/elif/else », qu’ils ont essayé d’adapter dans l’objectif de distinguer trois cas. Quatre élèves ont ainsi ajouté une condition à la branche « else » (« else var1==3 »). Lors de la tentative d’exécution qui suit, l’analyseur syntaxique de l’EDI remonte l’erreur suivante : « 'else' n'accepte pas de condition : utiliser 'elif' ». Ces quatre élèves ont par la suite simplement modifié « else » en « elif ». Il semblerait donc que la distinction des cas que permet la structure conditionnelle soit globalement comprise, en revanche le « court-circuit » qu’offre l’instruction « else » ne parait acquis que par un seul élève.

Ensuite, d’autres notions devaient obligatoirement être mises en œuvre pour la réussite des défis car rendues nécessaires par la logique interne de la situation. Dans ce cas, nous considérons également que si l’élève a réussi à mettre en œuvre la notion en jeu de manière autonome, c’est qu’il a pu acquérir des connaissances relatives à cette notion en lui donnant du sens. Nous avons rassemblé, dans le Tableau 3, pour chaque notion obligatoire contextualisée dans un défi, le nombre d’élèves l’ayant implémentée de manière autonome parmi les élèves ayant tenté le défi. Par exemple, pour la première ligne : le défi 1 nécessitait l’utilisation d’une fonction avec argument et avec retour, six élèves ont réussi à implémenter cette notion en autonomie parmi les six ayant tenté le défi.

Notions contextualisées	Implément.
D1N1 : utilisation d’une fonction avec arg. et sans retour.	6/6
D2A1N1 : utilisation d’une fonction avec arg. et sans retour.	6/6
D2A2N1 : utilisation d’une fonction avec arg. et sans retour.	5/5
D2A3N1 : utilisation d’une fonction avec arg. et sans retour.	6/6
D2A4N1 : utilisation d’une fonction avec arg. et sans retour.	6/6
D3N1 : utilisation d’une fonction avec arg. et sans retour.	6/6
D4N1 : utilisation d’une fonction avec arg. et sans retour.	6/6
D5N1 : utilisation d’une fonction avec arg. et sans retour.	5/5
D5A1N1 : utilisation d’une fonction avec arg. et sans retour.	3/3
D6A1N1 : utilisation d’une fonction avec arg. et sans retour.	3/3
D2A4N2 : utilisation d’une fonction avec arg. et avec retour.	3/6
D3N2 : utilisation d’une fonction avec arg. et avec retour.	5/6
D4N2 : utilisation d’une fonction sans arg. avec retour.	1/6
D5N2 : utilisation d’une fonction sans arg. avec retour.	2/5
D6A1N2 : définition d’une fonction sans arg. et sans retour.	3/3
D6A2N2 : définition d’une fonction avec arg. et sans retour.	0/3
D2A4N3 : affection et utilisation d’une variable.	4/6
D3N3 : affectation et utilisation d’une variable.	5/6
D4N4 : affectation et utilisation d’une variable.	4/6
D5N3 : affectation et utilisation d’une variable.	4/5
D5A2N3 : affectation et utilisation d’une variable.	2/3
D4N4 : boucle non-bornée.	5/6
D3N4 : branche conditionnelle « if ».	5/6
D5N4 : branche conditionnelle « if ».	4/5
D6A2N4 : branche conditionnelle « if ».	3/3
D5N5 : branche conditionnelle « elif ».	4/5
D4N5 : expression d’une chaîne de caractères	4/6
D6A2N7 : comparaison de chaînes de caractères	0/3

Notons d’abord que l’utilisation des fonctions ne semble pas poser de problème lorsqu’elles agissent sans retour (D1N1 -> D6A1N1 : 52/52 – 100%). Dès lors qu’elles retournent une valeur, les élèves parviennent plus difficilement à les utiliser en autonomie (D2A4N2 -> D5N2 : 11/23 – 47%). Lors de la définition des fonctions, c’est la gestion des arguments/paramètres qui entraine des difficultés de mise en œuvre (D6A2N2 : 0/3 – 0%). Nous pouvons avancer que les élèves savent utiliser une fonction, mais que leurs définitions et la gestion des entrées-sorties ne sont que partiellement acquises. Ensuite, l’utilisation de la boucle non-bornée (D4N4 : 5/6 – 83%), des branches conditionnelles « if » et « elif » (D3N4 -> D5N5 : 16/19 – 84%) et des variables (D2A4N3 -> D5A2N3 : 19/26 – 73%) s’effectue de façon relativement autonome. Nous pouvons arguer que les élèves ont réussi à intégrer l’utilité de ces notions, en les mobilisant à bon escient. Le typage des variables ne semble pas acquis en tant que tel, certains élèves ont été capables de délimiter des chaînes de caractères avec des guillemets (D4N5 : 4/6 – 67%) mais ont rencontré des difficultés lors des comparaisons de chaînes (D6A2N7 : 0/3 – 0%).

Au bilan, nous pouvons affirmer que notre séquence permet de réinvestir les notions introduites au cycle 4 (variables, boucles, conditionnelles) en leur conférant du sens, cependant elle ne permet pas la compréhension et l’intégration de tous les aspects des nouvelles notions prescrites en seconde (fonctions et typage).

L’enjeu consistait aussi à essayer de limiter la dilution des apprentissages algorithmiques prescrits dans quantité de nouveaux éléments de nature technique. En choisissant un environnement intégré dans lequel il suffit d’appuyer sur un bouton pour enregistrer le programme en cours d’édition, vérifier sa syntaxe, le téléverser sur la carte et lancer le programme à distance, nous dégageons l’élève de nombreuses considérations techniques. Cela semble d’abord avoir pour effet de limiter fortement les problèmes de nature technique qui font l’objet de seulement 5% (6/113) des interventions du professeur.

Cet EDI propose, de plus, un système d’analyse précoce et explicite des erreurs les plus courantes. Cela constitue une aide précieuse pour les élèves qui découvrent la contrainte de correction syntaxique du code. Ce système joue, d’une certaine manière, le même rôle que les détrompeurs des blocs Scratch empêchant les erreurs de syntaxe. Même si les erreurs sont encore bien présentes (157 occurrences lors de l’atelier), ce système permet aux élèves de gagner en autonomie. En effet, seules 13% (15/117) des erreurs repérées par l’EDI occasionnent une intervention du professeur contre 48% (19/40) des erreurs issues de l’interpréteur.

Concernant les entrées-sorties, le choix de permettre aux élèves d’interagir avec un dispositif physique permet de déporter les interactions avec le programme de la console vers la carte. En effet, il n’est pas nécessaire de saisir les entrées du programme dans la console, cela se fait en agissant directement avec la carte, de même les sorties ne se manifestent pas uniquement par des messages dans la console, elles peuvent prendre toutes les formes permises par la matrice de LED de la carte. On se rapproche, en ce sens, du fonctionnement du logiciel Scratch.

Le support pédagogique numérique permet aux élèves de pratiquer très largement le copier-coller (on dénombre sur l’ensemble de l’atelier 39 copier-coller de code depuis le support pédagogique vers l’EDI). L’utilisation de cette fonctionnalité de duplication diminue mécaniquement le nombre d’erreurs syntaxiques.

En définitive, nous proposons à travers cette expérimentation une solution équidistante entre l’approche de très haut niveau offerte par Scratch, entièrement tournée vers les concepts algorithmiques et la programmation Python de plus bas niveau qui expose davantage les élèves aux éléments techniques sous-jacents.

8.2. Paradigmes et méthodes de programmation : une étape intermédiaire

Nous avons constaté un changement dans les paradigmes et méthodes de programmation mis en œuvre par les langages Scratch et Python. Notre but était donc d’essayer d’accompagner ce passage d’une programmation évènementielle, orientée objet, et parallèle en Scratch à une programmation impérative et séquentielle en Python.

Lors de cet atelier, la majorité des défis avaient pour objectif de modifier l’état de l’objet « carte programmable » en accédant à ses méthodes : « get_presses() », « read_light_level() », « set_pixel() » ou encore « scroll() ». Ce genre d’approche, typique de la programmation orientée objet, se rapproche de celle de Scratch où il s’agit de modifier les propriétés d’objets « lutins » au moyen de ses méthodes : « avance », « tourne », « pense », « distance de ? », « touche ? » ou « volume sonore ? ».

Ensuite, les élèves sont amenés à lancer leur code à l’aide du bouton « reset » à l’arrière de la carte ou suite à l’actionnement des boutons à l’avant de celle-ci. On peut y voir des similitudes avec la programmation évènementielle mise en œuvre dans Scratch, où les programmes se lancent en réaction à des évènements.

Les multiples difficultés rencontrées par les élèves lors de la résolution du défi 4 (jeu de rapidité) proviennent pour partie du fait que cette situation n’était pas directement basée sur l’état de l’objet « carte », mais sur un compteur interne d’appuis. Ce type de problèmes relève d’une approche de la programmation plus séquentielle et impérative à laquelle les élèves ne sont pas accoutumés.

Nous pouvons, en résumé, affirmer, au regard des éléments avancés ci-dessus, que la séquence expérimentée au cours de cette ingénierie didactique, se veut être, ici aussi, une étape intermédiaire à mi-chemin entre deux paradigmes de programmation. Il faudra cependant, dans une deuxième phase, que les élèves se plient au paradigme impératif imposé par Python en classe de seconde.

8.3. Registres sémiotiques : une influence sur les apprentissages et une marge de manœuvre faible

Penchons-nous désormais sur les registres sémiotiques et l’influence sur les apprentissages des élèves du degré de congruence entre les différentes représentations des concepts en Scratch et Python. Notons qu’au moment de l’entretien, lorsque les élèves sont interrogés sur les liens qu’ils peuvent établir entre leurs activités habituelles en Scratch et ce qu’ils viennent de faire en Python, certains disent avoir remarqué des similitudes. D’abord concernant les concepts algorithmiques, quatre élèves font référence à la présence dans les deux langages de la structure conditionnelle et un à celle des boucles. D’autres éléments ressortent concernant les fonctions de service : le bloc « dire » est similaire à l’instruction « print() », le bloc « attendre » est équivalent à l’instruction « sleep() ». Trois élèves relèvent des concordances concernant la formulation impérative des instructions et la structuration des programmes : « c'est un peu dans la même logique, si on veut qu'il fasse ça, il faut faire une ligne de code alors que c'est un bloc d'habitude » et « la position des blocs sur Scratch, ils étaient décalés au fur et à mesure, et là aussi ». Les élèves sont donc en mesure d’établir des correspondances entre les deux langages. Cela permet, en particulier, de déceler chez eux des acquis notionnels antérieurs. Ces connaissances préalables constituent-elles une aide ou un obstacle dans l’apprentissage du langage Python ? Cela semble dépendre du degré de congruence entre les notions.

Ainsi, les acquis des élèves en Scratch doublés d’une congruence sémiotique moyenne-forte du concept de conditionnelle ont sans doute contribué à la réussite rapide (temps moyen de 16,7 minutes) et générale du défi 3 (pierre-feuille-ciseaux). À l’inverse, le défi 4 (jeu de rapidité), qui met en jeu le concept de boucle non-bornée ayant une très mauvaise congruence sémiotique, affiche un temps moyen de résolution de 47,5 minutes et donna lieu à de nombreuses difficultés. Nous avons, par exemple, pu relever des inversions de conditions (« jusqu’à » / « tant que ») symptomatiques dans les productions d’élèves.

Terminons en remarquant que notre marge de manœuvre était faible lors de la conception des activités. Au regard de notre analyse de congruence, les seuls leviers sur lesquels nous pouvions agir étaient de commencer par introduire la structure conditionnelle avec deux branches (congruence très forte dans ce cas contre moyenne avec trois branches) et de commencer avec des fonctions sans retour (congruence très forte contre moyenne pour les fonctions avec retour). Nous n’avons pas joué sur le premier paramètre ayant privilégié l’aspect ludique d’un jeu à « trois branches » (pierre-feuille-ciseaux), cela ne semble cependant pas avoir posé de problème aux élèves. Nous avons néanmoins agi sur le deuxième levier, et les résultats établis plus haut au sujet de l’utilisation autonome des fonctions sans retour semblent valider ce choix.

En résumé, les écarts sémiotiques entre les différentes représentations en Scratch et Python semblent avoir une influence sur la réussite des activités mais la marge de manœuvre dont nous disposions lors de leur conception était très faible est ne permettait pas de soutenir véritablement l’entrée dans le registre sémiotique des instructions.

8.4. Type d’activités : un fort engagement

En dernier lieu, nous avons anticipé une baisse dans l’engagement des élèves dans les activités de programmation proposées en classe de seconde, les problèmes proposés semblant plus scolaires et moins ludiques comparativement aux activités soumises aux collégiens. L’enjeu résidait donc dans le fait de pouvoir proposer, par le biais de différents artifices, des activités motivantes mettant en œuvre le langage Python.

Plusieurs indices nous font plaider en faveur d’un fort engagement des actants dans les activités proposées. À la fin des trois heures d’ateliers, plusieurs élèves expriment leur envie de continuer à programmer la carte chez eux. D’abord un élève qui, avant la fin, lance à un autre, installé une table devant lui : « Je vais faire ça chez moi, direct, je vais demander à mon frère de m’en acheter un ». Un troisième conclut, après s’être renseigné sur le prix de la carte sur Internet : « Eh bien, je m’achète ça quand j'arrive chez moi. ». Pendant l’entretien, lorsqu’il est demandé aux élèves s’ils seraient prêts à continuer chez eux si une carte leur était prêtée, ou s’ils conseilleraient l’atelier à d’autres personnes, ils répondent collectivement par l’affirmative.

Ensuite, en faisant remarquer aux élèves la durée de l’atelier, et en ajoutant que cela pouvait être long pour des collégiens, un élève réagit en disant : « Ah nan, c’était tranquille » et une autre ajoute : « Nan, en vrai, c’est passé vite ». Cette impression de temps qui « passe vite », indique, là aussi, un intérêt important pour le travail auquel ils venaient de prendre part. L’absence d’abandon en dépit des difficultés rencontrées par certains est aussi un élément allant dans ce sens.

Nous pouvons supposer que cet engagement dans les situations proposées est lié, pour partie, à la démarche de défi couplée à la présence de récompenses sous forme de badges. Certains éléments de l’entretien vont dans ce sens, une élève fait remarquer qu’« il fallait qu'on réfléchisse et qu'on essaye de comprendre pas nous-même et du coup bah, quand on trouvait, c'était satisfaisant on va dire », un autre complète en affirmant que « des p'tits badges, ça encourage ». Nous pouvons corroborer cette dernière déclaration par nos observations sur le terrain, ainsi, lors de l’atelier, les élèves ont réclamé leurs badges avec une certaine impatience lorsqu’ils leurs étaient dus et ils affichaient une certaine satisfaction lors de leurs remises.

Au final, nous pouvons avancer que la séquence que nous avons conçue favorise l’engagement dans les activités à la faveur du trio carte programmable-défis-badges.

9. Conclusion

En conclusion de cet article qui portait sur la programmation informatique à la transition collège-lycée, et en particulier sur le passage du logiciel Scratch au langage Python, nous allons d’abord en rappeler les principaux résultats. En suivant les principes méthodologiques de l’ingénierie didactique, nous avons débuté par une analyse préalable, qui nous a permis d’accréditer le fait que cette transition engendre des changements relatifs : aux contenus épistémiques, aux paradigmes de programmation, aux registres sémiotiques ainsi qu’aux types d’activités. Ces différences constituent, pour la plupart, des obstacles à franchir pour les élèves. Nous avons ensuite conçu une séquence d’enseignement dans l’objectif d’accompagner les élèves dans le dépassement de ces difficultés. À l’épreuve du terrain, nous avons ensuite constaté que ces activités permettent d’agir sur les contenus épistémiques : en offrant de réinvestir les notions introduites au cycle 4 (variable, boucle et conditionnelle) en leur conférant du sens, mais aussi en constituant une première approche des savoirs ciblés en seconde (typage et fonctions) sans pour autant permettre leur acquisition et leur compréhension profonde, enfin en estompant la surcharge des apprentissages algorithmiques par certains savoirs techniques. Cette séquence propose également une étape intermédiaire dans le changement de paradigme de programmation, elle favorise un fort engagement des élèves à travers l’utilisation du trio carte programmable-défi-badge mais ne parvient pas à soutenir véritablement l’entrée dans le registre sémiotique des instructions Python faute de leviers d’action suffisants.

Ces résultats doivent être considérés au regard des limites de notre méthodologie. Rappelons que les élèves qui ont participé à cette expérimentation sont volontaires, qu’ils montrent un intérêt préalable pour la programmation informatique, et qu’ils disposent déjà, pour certains, d’une petite expérience en la matière. Ils présentent tous un bon niveau scolaire général et de très bons résultats en mathématiques. Ce groupe de six élèves n’est donc pas représentatif d’une classe de trente-cinq élèves de seconde au niveau hétérogène et à l’intérêt variable pour l’informatique et la programmation. Notre méthodologie connaît d’autres imperfections, nous n’avons pas disposé d’assez de temps pour approfondir l’entretien avec les élèves, le double rôle professeur-chercheur est difficile à endosser pendant les expérimentations et pose la question de l’objectivité de l’analyse des activités du professeur.

Pour prolonger ce travail, il serait intéressant d’élargir le spectre de notre analyse préalable en la complétant par des analyses de terrain : ressources pédagogiques existantes (manuels scolaires, ressources numériques, etc.), observation de l’activité « ordinaire » des élèves en classe de troisième et de seconde. Il est également envisageable de concevoir une nouvelle itération de l’ingénierie basée sur les résultats du présent travail mais également sur les nouveaux éléments émanant de cette analyse préalable élargie ainsi que d’une revue de littérature plus poussée notamment au sujet des enjeux psychologiques et cognitifs liés aux langages de programmation, à la programmation tangible ainsi qu’à la ludification des activités. Enfin, cette nouvelle ingénierie pourrait être testée sur des classes en début de seconde dans des conditions écologiques.

REMERCIEMENTS

Ce travail a été soutenu par la Région Bretagne et l’Université de Bretagne Occidentale.

À propos des auteurs

Matthieu BRANTHÔME est doctorant en didactique de l’informatique à l’Université de Bretagne Occidentale (UBO) et est membre du Centre de Recherche sur l’Éducation, les Apprentissages et la Didactique (CREAD). Il a exercé quelques années dans l’industrie suite à l’obtention, en 2005, du diplôme d’ingénieur en informatique de l’INSA de Rennes. Après avoir enseigné les mathématiques, principalement au lycée, pendant une dizaine d’années, il obtient en 2020 le diplôme de master « recherches en didactique » de l’UBO. Ses travaux portent actuellement sur l’enseignement-apprentissage de la programmation informatique dans l’enseignement secondaire.

RÉFÉRENCES

Abramovich, S., Schunn, C. et Higashi, R. M. (2013). Are badges useful in education? It depends upon the type of badge and expertise of learner. Educational Technology Research and Development, 61(2), 217-232.

Artigue, M. (1988). Ingénierie didactique. Recherches en didactique des mathématiques, 9(3), 281-308.

Baron, G.-L. et Drot-Delange, B. (2016). L’informatique comme objet d’enseignement à l’école primaire française ? Mise en perspective historique. Revue française de pédagogie, 2, 51-62.

Bessot, A. (2003). Une introduction à la théorie des situations didactiques. Les cahiers du laboratoire Leibniz, 91, 1-28.

Blikstein, P. (2013). Gears of our childhood: Constructionist toolkits, robotics, and physical computing, past and future. Dans J. Hourcade, E. Miller et A. Egeland (dir.), Proceedings of the 12th international conference on interaction design and children (p. 173-182). ACM.

Brousseau, G. (1981). Problèmes de didactiques des décimaux. Recherches en Didactique des Mathématiques, 2(1), 37-125.

Brousseau, G. (1998). Théorie des situations didactiques : Didactique des mathématiques 1970-1990. La Pensée Sauvage.

Brousseau, G. (2010). Glossaire de quelques concepts de la théorie des situations didactiques en mathématiques. Disponible sur internet.

Caron, P.-A., Fluckiger, C., Marquet, P., Peter, Y. et Secq Y. (2020). Éditorial des actes du colloque. Dans P.-A. Caron, C. Fluckiger, P. Marquet, Y. Peter et Y. Secq (dir.), L’informatique, objets d’enseignements enjeux épistémologiques, didactiques et de formation. Actes du colloque DIDAPRO 8 – DIDASTIC (p. 6-10). Université de Lille.

Delmas-Rigoutsos, Y. (2020), Variables, grandeurs et types. Dans P.-A. Caron, C. Fluckiger, P. Marquet, Y. Peter et Y. Secq (dir.), L’informatique, objets d’enseignements enjeux épistémologiques, didactiques et de formation. Actes du colloque DIDAPRO 8 – DIDASTIC (p. 38-51). Université de Lille.

Dicheva, D., Dichev, C., Agre, G. et Angelova, G. (2015). Gamification in education: a systematic mapping study. Educational Technology & Society, 18(3), 75–88.

Duval, R. (1993). Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de didactique et de sciences cognitives, 5, 37-65.

Floyd, R. W. (1978). The paradigms of programming. Communications of the ACM, 22(8), 455-460.

Fluckiger, C. (2019). Une approche didactique de l’informatique scolaire. Presses universitaires de Rennes.

Gibson, D., Ostashewski, N., Flintoff, K., Grant, S. et Knight, E. (2015). Digital badges in education. Education and Information Technologies, 20(2), 403-410.

Hannula, M. S., Leder, G. C., Morselli, F., Vollstedt, M. et Zhang, Q. (2019). Affect and Mathematics Education: Fresh Perspectives on Motivation, Engagement, and Identity. Springer.

Hodges, S., Sentance, S., Finney, J. et Ball, T. (2020). Physical computing: A key element of modern computer science education. Computer, 53(4), 20-30.

Hudak, P. (1989). Conception, evolution, and application of functional programming languages. ACM Computing Surveys, 21(3), 359-411.

Kohn, T. (2017). Teaching Python programming to novices: Addressing misconceptions and creating a development environment [Thèse de doctorat]. ETH Zurich.

Journault, M., Lafourcade, P., Poulain, R. et More, M. (2020). Une preuve pour le lycée et l’indécidabilité du problème d’arrêt. Dans P.-A. Caron, C. Fluckiger, P. Marquet, Y. Peter et Y. Secq (dir.), L’informatique, objets d’enseignements enjeux épistémologiques, didactiques et de formation. Actes du colloque DIDAPRO 8 – DIDASTIC (p. 124-135). Université de Lille.

Khazaei, B. et Jackson, M. (2002). Is there any difference in novice comprehension of a small program written in the event-driven and object-oriented styles? Dans Proceedings IEEE 2002 Symposia on Human Centric Computing Languages and Environments (p. 19-26). IEEE.

Libert, C. et Vanhoof, W. (2020). Introduire la concurrence en début de seconde ? Dans P.-A. Caron, C. Fluckiger, P. Marquet, Y. Peter et Y. Secq (dir.), L’informatique, objets d’enseignements enjeux épistémologiques, didactiques et de formation. Actes du colloque DIDAPRO 8 – DIDASTIC, (p. 112-123). Université de Lille.

MEN. (2016). Ressource d’accompagnement en algorithmique et programmation du programme de mathématiques (cycle 4). Éduscol. Disponible sur internet.

MEN. (2017). Ressource d’accompagnement en algorithmique et programmation du programme de mathématiques de seconde. Éduscol. Disponible sur internet.

MEN. (2018). Programme d’enseignement cycle des approfondissements (Cycle 4). Dans Bulletin officiel n° 30 du 26 juillet 2018. MEN. Disponible sur internet.

MEN. (2019a). Préambule des ressources d’accompagnement en algorithmique et programmation du programme de mathématiques seconde et première. Éduscol. Disponible sur internet.

MEN. (2019b). Programme de mathématiques de seconde générale et technologique. Dans Bulletin officiel spécial n°1 du 22 janvier 2019. MEN. Disponible sur internet.

MEN. (2019c). Programme de sciences numériques et technologie de seconde générale et technologique. Dans Bulletin officiel spécial n°1 du 22 janvier 2019. MEN. Disponible sur internet.

Merkouris, A., Chorianopoulos, K. et Kameas, A. (2017). Teaching programming in secondary education through embodied computing platforms: Robotics and wearables. ACM Transactions on Computing Education, 17(2), 9:0-9:22

Papert, S. (1980). Mindstorms: Children, computers, and powerful ideas. Basic Books.

Przybylla, M. et Romeike, R. (2014). Key competences with physical computing. Dans T. Brinda, N. Reynolds, R. Romeike et A. Schwill (dir.) KEYCIT 2014–Key Competencies in Informatics and ICT (p. 351-361). University of Potsdam.

Rogalski, J. (2015). Psychologie de la programmation, didactique de l'informatique : déjà une histoire... Dans G.-L. Baron, E. Bruillard et B. Drot-Delange (dir.), L'informatique en éducation : perspectives curriculaires et didactiques (p. 279-305). Presses Universitaires Blaise Pascal.

Rubio, M. A., Hierro, C. M. et Pablo, A. (2013). Using arduino to enhance computer programming courses in science and engineering. Dans L. Gómez Chova, A. López Martínez et I. Candel Torres (dir.), Proceedings of EDULEARN13 conference (p. 5127-5133). IATED.

Sentance, S., Waite, J., Hodges, S., MacLeod, E. et Yeomans, L. (2017). Creating Cool Stuff: Pupils’ Experience of the BBC micro: Bit. Dans Proceedings of the 2017 ACM SIGCSE Technical Symposium on Computer Science Education (p. 531-536). ACM.

Sentance, S., Waite, J., Yeomans, L. et MacLeod, E. (2017). Teaching with physical computing devices: The BBC micro: Bit initiative. Dans E. Barendsen et P. Hubwieser (dir.), Proceedings of the 12th Workshop on Primary and Secondary Computing Education (p. 87-96). ACM.

Stefik, M. et Bobrow, D. G. (1985). Object-oriented programming: Themes and variations. AI magazine, 6(4), 40-62.

Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive science, 12(2), 257-285.

White, G. et Sivitanides, M. (2005). Cognitive differences between procedural programming and object oriented programming. Information Technology and management, 6(4), 333-350