Un système d’aide à l’analyse des traces des apprenants dans les jeux sérieux

Mathieu MURATET, Amel YESSAD, Thibault CARRON, Arthur RAMOLET

Mathieu MURATET (Sorbonne Université, CNRS, INS HEA, LIP6, F-75005 Paris, France), Amel YESSAD (Sorbonne Université, CNRS, LIP6, F-75005 Paris, France), Thibault CARRON (Sorbonne Université, CNRS, Université Savoie Mont Blanc, LIP6, F-75005 Paris, France), Arthur RAMOLET (Sorbonne Université, CNRS, LIP6, F-75005 Paris, France)

1. Introduction

Le suivi des apprenants est une problématique importante du domaine des Environnements Informatiques pour l'Apprentissage Humain (EIAH). En particulier, les traces produites par les apprenants dans les environnements de formation interactifs tels que les jeux sérieux sont complexes et volumineuses et par suite difficiles à analyser. Il est donc utile de doter les enseignants d'outils capables d'analyser ces traces et de leur fournir un retour leur permettant de mieux interpréter le comportement des apprenants, pour éventuellement leur apporter une aide adaptée. Notre approche vise à fournir un ensemble d'informations pédagogiques sur le comportement d'un apprenant évoluant dans un environnement complexe. Ces informations sont calculées en comparant la trace de l’apprenant avec un modèle des solutions fournies par les experts. Dans cet article nous entendons par « expert » l’ensemble des personnes détenant l’expertise du jeu sur ses dimensions ludiques et pédagogiques, ceci inclut donc les experts du domaine ainsi que les concepteurs du jeu.

Nous axons notre recherche sur les jeux sérieux simulant des processus métiers complexes dans des domaines tels que la physique, la biologie, l’économie, etc. Ces processus présentent souvent une explosion combinatoire de leurs espaces d'états due à une grande liberté d'interaction des apprenants, ce qui rend compliqué le suivi par les enseignants. Ainsi, notre objectif était de générer une description lisible du comportement des apprenants à destination des enseignants ou de toute autre personne désirant analyser leur comportement (les tuteurs, les concepteurs de jeux, les joueurs eux-mêmes, etc.).

L'architecture globale que nous présentons dans cet article est composée de deux parties : le processus permettant la construction assistée du modèle qui intègre les solutions référencées par les experts (que nous appelons dans la suite solutions expertes) et le système Laalys V2 (Learner Activity AnaLYSer) qui permet le suivi des apprenants à partir de l'analyse de leurs traces.

Concernant la construction assistée du modèle intégrant les solutions expertes, notre proposition exploite le formalisme des réseaux de Petri (RdP). Avec cette approche, la difficulté majeure rencontrée lors de la conception d’un jeu sérieux résidait dans la construction du RdP lui-même. Cette étape était réalisée « à la main » et de nombreuses itérations étaient nécessaires afin de converger vers un modèle satisfaisant, formalisant la simulation du jeu et intégrant les solutions expertes de résolution du problème. Notre contribution consiste donc à proposer une méthode accompagnée d’outils pour assister la création des RdP.

Concernant le système Laalys V2, la contribution présentée dans cet article concerne l'algorithme qui exploite le RdP afin d’associer des étiquettes pédagogiques aux actions d'un apprenant et de calculer un score à partir de ces étiquettes. Ces dernières renseignent les utilisateurs et notamment les enseignants sur le comportement d'un apprenant en qualifiant, par exemple, ses actions comme étant correctes, erronées, tardives ou prématurées. Le principe de cet algorithme d'étiquetage est de fournir des informations sémantiques sur les écarts détectés entre la résolution de l'apprenant et celles des experts. Nous avons mené une expérimentation avec des élèves et des enseignants de collèges dans le but d'évaluer la pertinence des étiquettes automatiquement identifiées par l’algorithme.

Dans la section suivante, nous dressons un panorama des recherches récentes en lien avec notre travail. Ensuite nous présentons de manière générale la méthode proposée, ce qui nous permet d’introduire les deux contributions de cet article. La section 4 présente la première contribution, à savoir les outils d’aide à la construction du modèle des solutions expertes. Dans la section 5, nous présentons la seconde contribution de cet article, à savoir l'algorithme d'étiquetage des actions de l'apprenant. Dans la section 6, nous décrivons l'expérimentation menée et les résultats obtenus. Enfin, nous concluons l'article en mettant en avant quelques perspectives que nous considérons pertinentes pour la suite de ce travail.

2. Travaux similaires

Le travail de recherche présenté dans cet article est une contribution à la problématique du suivi des apprenants dans les jeux sérieux. De nombreux travaux utilisant des techniques d'intelligence artificielle (dont la fouille de données) analysent les traces des apprenants en vue de fournir un feedback aux enseignants (Kosba et al., 2007), (Baradwaj et Pal, 2012), (Angeli et Valanides, 2013), (Azevedo et al., 2013). Cependant, peu de travaux ont été réalisés dans le cadre de systèmes intégrant de la simulation de processus métiers complexes, tels que les jeux sérieux auxquels nous nous sommes intéressés.

Pour de tels systèmes, des recherches ont été menées dans le domaine de la visualisation de l'information, afin de fournir aux enseignants les moyens d’explorer des représentations graphiques pour identifier les informations nécessaires à leurs activités pédagogiques. Par exemple, les travaux présentés dans (Medler et al., 2011) et (Wallner et Kriglstein, 2014) se sont focalisés sur des indicateurs visuels de jeu et consistent à collecter de manière extensive les données des joueurs pendant le jeu pour guider la prise de décision. Ils visent à fournir à la fois une analyse du gameplay et des traces d'exécution des joueurs en s'appuyant sur le temps et le séquencement. Ces travaux ne se sont toutefois pas intéressés à la définition d’indicateurs liés au comportement des joueurs dans le domaine de l'éducation ce qui est justement le point central de notre travail. Dans notre approche, le système analyse le comportement des apprenants et étiquète leurs actions avec des métadonnées pédagogiques. L'objectif est de fournir un retour aux enseignants sur le comportement des apprenants utilisant des jeux sérieux avec de grands espaces d’états. Cela correspond à des jeux qui offrent une grande liberté d’actions aux joueurs. Par exemple, face à un problème, ces derniers doivent déterminer la bonne séquence d’actions à effectuer parmi de nombreuses séquences d’actions possibles.

Des travaux similaires aux nôtres ont été proposés par (Harpstead et al., 2013). Les auteurs proposent une méthodologie pour extraire des caractéristiques conceptuelles des traces des apprenants et les utilisent pour classifier les apprenants dans des groupes. Bien que la finalité soit différente, car les auteurs visent à exploiter les traces des étudiants à des fins de réingénierie, leur problématique reste similaire : aider à comprendre l’ensemble des solutions des apprenants. Dans notre contexte, où nous souhaitons fournir aux enseignants des informations pédagogiques sur la manière dont les apprenants ont résolu le problème, cette approche s’est révélée non adaptée car elle se base uniquement sur la production finale de l’apprenant et ne prend pas en compte le processus de résolution.

Dans les travaux de (Blanco et al., 2010), les auteurs associent aux jeux des machines à états qui représentent uniquement les situations que les enseignants souhaitent observer. Ils sélectionnent ainsi a priori les états qu'ils souhaitent tracer. Cette approche apporte une solution pour réduire la complexité de l’analyse mais pose deux problèmes majeurs. D’une part, elle nécessite a posteriori un effort important de la part des enseignants pour interpréter les indicateurs calculés par le système et, d’autre part, les enseignants pourraient ne pas observer des comportements intéressants réalisés par leurs élèves.

D’autres recherches s’appuient sur les réseaux de Petri pour modéliser la résolution des experts et proposent un algorithme pour étiqueter les actions des apprenants (Yessad et al., 2010) et (Thomas et al., 2012). Cependant, cet algorithme est seulement adapté aux jeux de type « étude de cas » et ne convient pas à des jeux sérieux impliquant de très grands espaces d'états et une grande liberté d’action des utilisateurs. Nos travaux s'inscrivent dans la continuité de ces recherches mais visent à proposer un environnement plus générique et capable de supporter le passage à l'échelle en vue de fournir des informations d'ordre pédagogique sur le comportement de l'apprenant. Ces étiquettes pédagogiques, conçues avec des enseignants, sont plus compréhensibles par eux et sont basées sur la comparaison entre le comportement des apprenants et les comportements des experts, tous résolvant un même niveau de jeu. Une autre contribution importante de notre approche est la construction assistée du modèle de résolution de l'expert à partir d'une description déclarative et de haut niveau des niveaux de jeu.

3. Vue générale des processus de traitement

Le travail décrit dans cet article a pour objectif de présenter une approche d'analyse du comportement d'un apprenant au sein des jeux sérieux. Le système de suivi que nous proposons est basé sur la comparaison entre les traces de l’apprenant et la (les) solution(s) proposée(s) par des experts et modélisée(s) par un RdP. Une méthode de conception a été mise en place pour aider à la construction de ce réseau.

La figure 1 illustre les différents processus permettant de mettre en place le suivi des apprenants. Pour atteindre notre but, nous construisons deux RdP. Le premier RdP modélise toute la simulation du jeu incluant toutes les actions que l’apprenant peut exécuter dans le jeu et est appelé « Réseau de Petri complet » (RdpComplet). Le deuxième réseau de Petri appelé « Réseau de Petri filtré » (RdpFiltré) est une partie du RdpComplet incluant uniquement les actions que les experts ont utilisées pour résoudre le niveau du jeu.

Pour parvenir au RdpFiltré, les concepteurs disposent d'un système auteur (intégré à l’environnement de développement Unity) qui leur permet, avec l’aide de l’expert, de décrire les entités du jeu et leurs propriétés (par exemple, une entité « porte » peut être ouverte ou fermée, une flaque d'eau peut se transformer en glace ou s'évaporer). Une fois, les entités du jeu décrites, le RdpComplet est généré automatiquement et le jeu sérieux doté d’un module de production de traces est exporté. Le ou les experts peuvent alors jouer le jeu (plusieurs fois si plusieurs solutions « recommandées » existent pour un même niveau de jeu) et leurs actions sont tracées par le moteur du jeu. Ces traces sont utilisées pour filtrer le RdpComplet et générer ainsi le RdP filtré (RdpFiltré).

Après avoir présenté cette vue générale du processus de traitement, nous présentons en détail les deux contributions de cet article, à savoir, le processus d’aide à la construction des RdP et l’algorithme d’étiquetage exploitant ces RdP.

4. Processus d'aide à la construction du modèle des solutions expertes

Comme nous l’avons exposé précédemment, nous exploitons les réseaux de Petri pour modéliser les solutions expertes d’un jeu sérieux. Nous avons choisi d’exploiter les RdP car ils ont montré depuis longtemps leur capacité à modéliser des systèmes extrêmement complexes avec de grands espaces d'états, et notamment les jeux sérieux (Araújo et Roque, 2009). Le formalisme des RdP s’appuie à la fois sur une théorie mathématique formelle rendant le modèle traitable par la machine et sur une représentation graphique lisible par des humains.

4.1. Intérêt du formalisme des réseaux de Petri (RdP)

Formellement, un RdP est un graphe biparti, valué et composé de deux types de nœuds : des places et des transitions. Chaque arc permet de connecter une place à une transition ou une transition à une place. Les places sont marquées et contiennent un nombre de jetons positif ou nul. Le vecteur qui associe à chaque place son marquage est appelé marquage du RdP et représente son état à un instant T. Une transition du RdP peut être exécutée si elle est sensibilisée, c'est-à-dire, si chacune de ses places d'entrée satisfait la contrainte définie par le type et le poids de l'arc qui la relie à cette transition. Lorsqu'une transition est exécutée, des jetons des places d’entrée sont consommés (en fonction du type de l’arc) et d'autres jetons sont ajoutés aux places de sortie. L'ensemble des marquages atteignables à partir du marquage initial du RdP en exécutant les transitions sensibilisées représente l'ensemble des états du système et est appelé le graphe d'accessibilité. C’est ce dernier que nous exploitons pour analyser les actions du joueur. Dans le cas où le nombre d’états du jeu est infini, le graphe d’accessibilité ne peut pas être calculé et est remplacé par un autre graphe appelé graphe de couverture (GC). Les jeux sérieux sur lesquels nous travaillons ont souvent des graphes d’accessibilité infinis et donc, pour les besoins de l’analyse, l’algorithme calcule leur GC. Pour plus de détails, nous invitons le lecteur à consulter la littérature sur les réseaux de Petri (Peterson, 1981).

Dans notre cas, les places du RdP qui modélise un jeu sérieux représentent les différents états des objets du jeu et les transitions du RdP représentent les actions que l’apprenant peut exécuter dans le jeu pour passer d’un état à un autre. Ainsi la réalisation d’actions de jeu peut être simulée dans le réseau de Petri en déclenchant la transition associée à l’action du joueur, modifiant ainsi l’état du réseau.

Plus précisément, nous utilisons une sous-classe des RdP incluant des arcs inhibiteurs. Ces arcs ont la propriété d’inhiber une transition si le nombre de jetons inclus dans la place source est égal ou supérieur au poids de l’arc. Ce type d’arcs est intéressant dans notre contexte car il permet de modéliser le fait que certaines actions de jeu peuvent ne plus être possibles si l’état de la simulation dépasse certaines limites. Par exemple, considérons un jeu simple où le joueur peut subir des attaques, réduisant ses points de vie de 1, et se soigner en augmentant ses points de vie de 10. Le joueur peut se soigner seulement si ses points de vie sont strictement inférieurs à 91 (pour ne pas dépasser un maximum de 100 points de vie en cas de soin). Dans cet exemple, l’utilisation d’un arc inhibiteur évite d’avoir à créer une place artificielle stockant le nombre de points de vie perdus (voir figure 2). L’économie de la création de cette place artificielle est importante dans notre cas, car elle évite une intrication de l’action de soin avec une autre action de jeu, l’attaque dans cet exemple. Notre objectif étant d’assister la construction du réseau de Petri, l’utilisation des arcs inhibiteurs permet de simplifier le travail des concepteurs. En effet, dans cet exemple, les concepteurs pourront exprimer la contrainte sur l’action de soin sans avoir à se préoccuper des effets de bords sur d’autres actions de jeu (voir section 4.3 pour les détails sur l’expression de ces contraintes).

Figure 2 • Modélisation d’un système d’attaque/soin avec un arc inhibiteur (a) et sans arc inhibiteur (b)

L’utilisation des arcs inhibiteurs a toutefois des implications sur les algorithmes permettant d’exploiter et d’analyser les réseaux de Petri qui génèrent un nombre d’états potentiellement infini (Busi, 2002). Nous avons donc développé un algorithme permettant de calculer et d’exploiter le graphe de couverture d’un RdP qui prend en compte les arcs inhibiteurs et leur poids. Dans cet article, nous ne rentrons pas dans les détails d’implémentation de cet algorithme, mais nous en présentons néanmoins les points clés.

Comme évoqué précédemment, un graphe de couverture (GC) est une approximation finie de l’ensemble des marquages (potentiellement infini) du RdP et des séquences d’actions permettant de les atteindre. Le GC est calculé lorsqu’il est impossible de calculer le graphe d’accessibilité en raison de l’infinité des marquages atteignables. L’idée générale consiste à factoriser les marquages pour lesquels seul le contenu d’une place augmente. Le problème dans le cas des arcs inhibiteurs est la perte de la propriété de monotonie, définie ainsi : si une séquence de transitions est activable pour un marquage donné alors elle le sera aussi pour n’importe quel marquage englobant¹. Or, les arcs inhibiteurs contredisent cette propriété puisque l’augmentation du marquage par un arc inhibiteur aura justement pour effet d’inhiber des transitions. Pour résoudre ce problème nous construisons un graphe de couverture semi-développé incluant l’ensemble des marquages inférieurs au poids maximum des arcs inhibiteurs. Ceci a pour effet d’augmenter le nombre d’états du graphe de couverture mais rétablit la propriété de monotonie lorsque ce seuil est atteint.

Nous exploitons le graphe de couverture pour vérifier différentes propriétés. Par exemple, nous vérifions si une action du joueur est réalisable dans la suite de la simulation du système (l’action correspond à une transition franchissable) ou a déjà été réalisée (l’action correspond à une transition déjà franchie), ou nous vérifions si le joueur est bloqué (l’état final du système n’est pas atteignable à partir de l’état courant).

Nous utilisons ainsi le formalisme des RdP pour modéliser la dynamique des jeux sérieux et le graphe d’accessibilité (ou le GC dans le cas d’un graphe d’accessibilité infini), calculé automatiquement à partir du RdP, pour vérifier des propriétés sur les actions du joueur. Naturellement, le goulot d’étranglement de notre approche réside dans la construction du RdP, qui était initialement manuelle. Dans la suite de l’article, nous présentons le framework qui permet de réduire le temps et l’effort de cette construction en assistant la construction du RdP du jeu. Pour atteindre cet objectif, nous nous appuyons sur l’architecture logicielle Entité-Composant-Système que nous utilisons pour développer nos jeux sérieux. Dans la section suivante, nous présentons brièvement cette architecture avant d’expliquer comment nous l’utilisons pour produire le RdP du jeu sérieux.

4.2. Intérêt de l’architecture logicielle Entité-Composant-Système

L’Entité-Composant-Système (ECS) est une architecture logicielle principalement utilisée pour le développement de jeux vidéo (Bilas, 2002) et (Capdevilla, 2013). Le principe de cette architecture consiste à séparer les données de leur traitement. Les entités représentent des objets dans le jeu et ne contiennent pas de données propres ni de méthodes (ou fonctions). Les composants sont des propriétés des entités représentant leurs différentes facettes. Par exemple, la couleur est un composant, la position est un composant, etc. Une entité est donc définie par l’ensemble des composants qui la caractérisent. De leur côté, les systèmes contiennent la logique du jeu et accèdent aux composants des entités en vue de les mettre à jour (par exemple : changer la position d’une entité ou sa couleur) et ainsi faire évoluer la simulation du jeu.

L’intérêt de cette architecture pour le jeu vidéo repose sur le fait que le processus de création d’un jeu vidéo est hautement itératif et non prédictible. En effet lors du développement d’un jeu vidéo, de nombreuses fonctionnalités peuvent être ajoutées de manière incrémentale par les game designers, ce qui peut mettre à mal l’arbre d’héritage d’une architecture classique orientée objets. Par exemple, doter une entité de nouvelles propriétés peut poser problème et remettre en cause l’arbre d’héritage initial, en particulier lorsque l’héritage multiple n’est pas supporté par le langage de programmation utilisé. L’approche par composition telle que définie par l’architecture ECS permet de mieux gérer ces problèmes d’évolution du système. Ainsi, l’ajout de nouvelles fonctionnalités consiste simplement à : (1) définir les composants stockant les données relatives à cette nouveauté ; (2) relier ces composants aux entités concernées ; et (3) implémenter les systèmes permettant de traiter ces composants.

En nous appuyant sur (Capdevilla, 2013), nous avons implémenté notre ECS comme un plugin à l’environnement de développement Unity² (https://unity3d.com/fr). Nous souhaitions en effet bénéficier des avantages de l’outil auteur d’Unity et de ses différents moteurs existants (rendu, physique, réseau, etc.) tout en profitant des avantages de l’architecture ECS. Notre implémentation open source de l’architecture ECS se nomme FYFY (FamilY For unitY, - https://github.com/Mocahteam/FYFY). Dans cette implémentation nous intégrons le concept de « famille ». Une famille est définie comme un ensemble de critères permettant de filtrer les entités (présence ou absence d’un ensemble de composants par exemple). La famille est donc l’objet permettant aux systèmes de définir de manière fine l’ensemble des entités qu’ils doivent traiter.

L’architecture ECS augmentée du concept de famille nous permet d’intégrer le suivi, soit au niveau d’une entité (suivi microscopique), soit au niveau d’une famille (groupe d’entités – suivi macroscopique). La section suivante détaille cet aspect.

4.3. Exploitation de l’architecture logicielle Entité-Composant-Système pour assister la construction de réseaux de Petri

Dans le but de mettre en place un système de suivi des apprenants dans les jeux sérieux, nous avons fait le choix d'assister les concepteurs du jeu dans la construction des réseaux de Petri. En effet, la construction manuelle d’un réseau de Petri modélisant l’ensemble des entités à suivre et leurs relations est une tâche extrêmement complexe et représente le goulot d’étranglement de notre approche. Notre démarche consiste à demander aux concepteurs du jeu de créer à la main des RdP simples. Un RdP simple représente un pattern de comportement générique qu’on peut associer à une entité isolée sans se préoccuper des dépendances qu’elle peut avoir avec les autres entités. Nous avons ainsi construit, en tant que concepteurs du jeu, un ensemble de réseaux génériques représentant ces patterns de comportements récurrents dans les jeux, comme des objets de jeu activables ou des objets de jeux ramassables, l’objectif étant de capitaliser ces réseaux simples afin d’éviter d’avoir à les recréer pour chaque nouveau jeu. La figure 3 présente les deux exemples cités précédemment.

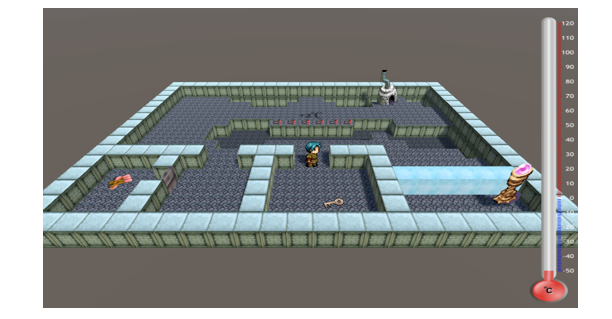
Figure 3 • Modélisation d’un objet activable (a) et d’un objet ramassable (b) à l’aide de réseaux de Petri simples

Ces RdP simples peuvent alors être reliés soit à une entité concrète du jeu, pour mettre en place un suivi particulier sur cette entité, soit à une famille, pour mettre en place un suivi global sur l’ensemble des entités de cette famille. Reprenons l’exemple d’un objet activable : si nous relions un réseau simple à une entité précise, nous pourrons suivre son état de manière fine car nous savons que cette entité peut être active (respectivement inactive) si le joueur l’active (respectivement la désactive). Si nous relions le même réseau à une famille d‘entités activables, nous suivrons alors globalement l’ensemble des entités de cette famille. Afin d’assister la construction du RdP du jeu, qui modélise les dépendances entre les entités suivies, nous avons conçu et implémenté une IHM qui permet aux concepteurs d’exprimer ces dépendances à l’aide d’un pseudo-langage.

La figure 4.a présente une situation de jeu dans laquelle le joueur doit ouvrir une porte gelée pour résoudre le niveau ; il dispose dans la scène d’une clé et d’une chaudière. Nous utilisons cet exemple pour illustrer le processus de construction assistée d’un RdP. Nous avons relié le RdP « ramassable » à la clé et le RdP « activable » à la porte et à la chaudière. Nous paramétrons ensuite la porte pour contraindre son activation (ouverture) au fait que la chaudière soit activée (allumée) ET que la clé soit en main. Le réseau complet de cette situation de jeu peut alors être généré automatiquement (voir figure 4.b) à partir des réseaux simples associés à chaque entité et des dépendances décrites entre les entités via l’IHM. Si nous avions contraint l’ouverture de la porte par la nécessité d’avoir la chaudière allumée OU la clé en main, le réseau final aurait été différent (voir figure 5).

Figure 4 • (a) Capture d’écran de la mission du jeu « La porte gelée » et (b) son réseau de Petri généré automatiquement

Figure 5 • Réseau de Petri généré automatiquement avec une contrainte de type OU sur l’ouverture de la porte

Une dépendance ou un lien entre deux entités d’un jeu implique, suivant les cas, de connecter une transition du RdP de la première entité à une place de la deuxième entité ou inversement. Ce fonctionnement est bien entendu généralisé dans le cas de trois entités ou plus. Au niveau de l’IHM que nous proposons, l’expression d’un lien suit le schéma suivant :

• sélection de l’action (la transition) à connecter (appartenant à une première entité) ;

• sélection de l’état (la place) à connecter à cette action (appartenant à une deuxième entité) ;

• un lien de type « Get », traduit dans le RdP par un arc qui consomme de la place sélectionnée un nombre de jetons égal au poids du lien ;

• une contrainte de type « at least » : traduit dans le RdP par un arc « read » qui ne consomme pas de jetons mais active la transition si le nombre de jetons dans la place sélectionnée est supérieur ou égal au poids du lien ;

• une contrainte de type « less than » : traduit dans le RdP par un arc inhibiteur qui ne consomme pas de jeton mais désactive la transition si le nombre de jetons dans la place est supérieur ou égal au poids du lien.

• un lien de type « Produce », traduit dans le RdP par un arc qui produit dans la place sélectionnée un nombre de jetons égal au poids du lien.

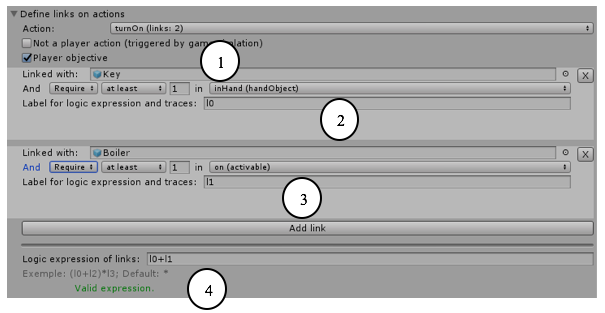
Si plusieurs liens sont définis sur une même action, ils peuvent être combinés à l’aide d’une expression booléenne. L’opérateur « * » (ET) applique tous les liens sur la transition considérée alors que l’opérateur « + » (OU) duplique la transition considérée afin de n’appliquer à chaque transition que les liens concernés. La figure 6 présente une capture d’écran du module « Monitoring » intégré à FYFY qui a permis de générer le réseau de Petri présenté en figure 5. Elle illustre le lien défini par le concepteur entre l’action turnOn (Activer) (1) de l’entité Porte avec les états inHand (en main) de l’entité Key (Clé) noté « l0 » (2) et on (Activé) de l’entité Boiler (Chaudière) noté « l1 » (3). Au moins un de ces deux liens est requis pour ouvrir la porte d’où l’expression : « l0+l1 » (4).

Le module « Monitoring » de FYFY permet d’intégrer à Unity les fonctionnalités suivantes :

Nous venons de présenter dans cette section l’ensemble des outils que nous proposons pour aider à la construction du RdP modélisant le comportement des entités du jeu et leurs dépendances. Ce réseau de Petri constitue le RdpComplet tel que défini dans la section 3. Le RdpFiltré est ensuite généré à partir du RdpComplet en ne conservant que les actions utilisées par les experts pour résoudre le niveau du jeu. Dans la suite de l’article le graphe d’accessibilité/couverture calculé à partir du RdpFiltré est noté espace-f. Cette étape de filtrage peut avoir deux conséquences éventuelles. Premièrement, des solutions intéressantes peuvent être exclues de l’espace-f . Dans ce cas, des traces non-expertes mais considérées comme intéressantes pourraient également être utilisées pour filtrer le RdpComplet ; par exemple, une solution originale et correcte faite par un apprenant et évaluée positivement par l'enseignant peut être ajoutée aux traces expertes pour élargir l'éventail de solutions présentes dans le RdpFiltré. Deuxièmement, des séquences d’actions qui ne constituent pas des solutions peuvent rester dans l’espace-f ; en effet, toute combinaison d’actions de jeu sélectionnées par l’expert ne constitue pas forcément une solution valide du problème posé. L’algorithme présenté dans la section suivante vise à identifier ces cas et à labelliser les actions des apprenants en conséquence.

5. Analyse du comportement de l'apprenant

Comme défini dans la section précédente, nous nous appuyons sur deux réseaux de Petri pour l’analyse du comportement de l’apprenant : le premier (RdpComplet) modélise la simulation complète d'un niveau de jeu alors que le second (RdpFiltré) est une partie du premier et n’intègre que les actions recommandées par les experts pour résoudre un niveau de jeu. L’analyse du comportement d’un apprenant consiste à étiqueter ses actions. Nous proposons un algorithme permettant cet étiquetage.

5.1. Algorithme d’étiquetage

Les entrées de l'algorithme d’étiquetage sont le RdpFiltré et la trace d'un apprenant. L'algorithme d’étiquetage s'appuie sur l'identification des 3 cas suivants : le premier cas correspond aux situations dans lesquelles l’apprenant a réalisé des actions qui sont refusées par le jeu et donc qui ne modifient pas l'état du jeu ; le deuxième cas correspond aux situations où l’apprenant a réalisé des actions qui sont acceptées par le jeu et donc en modifient l'état ; le troisième et dernier cas correspond à l'identification des actions manquantes alors que le jeu est terminé.

Chacun de ces cas mène à une description qui permet de caractériser l'action de l'apprenant au moyen d'une (et d'une seule) étiquette pédagogique.

5.1.1. Cas 1 - actions qui ne changent pas l'état du jeu

Ce cas apparaît lorsque l'apprenant essaie de réaliser une action qui n'est pas autorisée dans l'état actuel du jeu, par exemple, si le joueur tente d'ouvrir une porte alors qu'il n'a pas la bonne clé. Nous avons identifié quatre étiquettes spécifiques pour caractériser ces actions de manière plus précise :

• « Tardive » si l'action était exécutable dans un état antérieur du jeu ;

• « Prématurée » si l'action sera exécutable dans un état postérieur du jeu ;

• « Non synchronisée » si l'action a été exécutable et le sera à nouveau plus tard ;

• « Erronée » si cette action n'est jamais réalisée par les experts dans la résolution du niveau.

5.1.2. Cas 2 - actions qui changent l'état du jeu

Cela correspond au cas le plus courant, mais toutefois toutes les actions ne sont pas forcément correctes en comparaison avec la résolution des experts. En effet, la plupart des jeux pour apprendre permettent à l’apprenant de faire des erreurs. Ce principe d'essai/erreur est au cœur des jeux vidéo (Gee, 2007). L'opportunité de réaliser des séquences d'actions inutiles, redondantes ou incorrectes dans un jeu sérieux (Young, 2009) (Thomas et al., 2011) est fondamentale afin d’initier un processus de réflexion libre chez les apprenants et tenter d'atteindre les objectifs pédagogiques visés. L'algorithme évalue donc si le nouvel état courant du jeu quitte l'espace-f, revient dans l’espace-f, se déplace à l'intérieur de l’espace-f ou se déplace en dehors de l’espace-f.

5.1.2.1. Cas 2.1 - sortie de l’espace-f

Ce cas peut apparaître quand l'apprenant joue une action qui n'a pas été réalisée par les experts. Si l'état du jeu est en-dehors de l’espace-f, cela signifie que l'état du jeu généré ne correspond à aucun des états présents dans l’espace-f. L’étiquette utilisée pour étiqueter cette action est « Erronée ».

5.1.2.2. Cas 2.2 - retour vers l’espace-f

Cela correspond au moment où l'apprenant corrige de précédentes erreurs et retourne dans l’espace-f. Dans ce cas, l'algorithme (1) vérifie si l'état du jeu (noté e) résultant de l'action de l'apprenant est inclus dans l'historique des états déjà atteints par l’apprenant (noté Hist), (2) calcule la longueur du plus court chemin entre ce nouvel état et un état final (noté Lpcc) et (3) évalue la distance minimale (plus court chemin) entre chaque état de l'historique et un état final (noté Dmin). En fonction des résultats sur ces trois critères, les étiquettes suivantes sont générées pour l'action de l’apprenant :

5.1.2.3. Cas 2.3 - déplacement dans l’espace-f

Dans ce cas, l'algorithme vérifie si l’apprenant progresse vers un état final ou tend à s'en éloigner. Ainsi l'algorithme (1) calcule la longueur du plus court chemin (noté Lpcc) entre le nouvel état (noté ne) et un état final (noté ef), (2) évalue la longueur du plus court chemin entre l'état précédent (noté ep) et un état final, (3) vérifie si ces deux chemins (noté Pcc) sont différents, (4) vérifie si l'action effectuée est une action experte (noté Expert) et (5) vérifie si le nouvel état est un successeur direct de l'état précédent dans l’espace-f (noté Succ).

En fonction des résultats sur ces cinq critères, les étiquettes suivantes sont générées pour l'action de l'apprenant :

• « Equivalente » (¬Expert ∧ (Lpcc(ne, ef) < Lpcc (ep, ef)) ∧ Succ) ;

• « Progression » ((¬Expert ∧ (Lpcc(ne, ef) < Lpcc (ep, ef)) ∧ ¬Succ) ;

• « Inutile » ((Lpcc(ne, ef) = Lpcc (ep, ef)) ∧ (Pcc(ne, ef) = Pcc(ep, ef))) ;

• « Non-optimale » (((Lpcc(ne, ef) = Lpcc (ep, ef)) ∧ (Pcc(ne, ef) ≠ Pcc(ep, ef)) ;

5.1.2.4. Cas 2.4 - déplacement en dehors de l’espace-f

Ce comportement correspond au cas où l’apprenant réalise une action qui conserve le jeu dans un état en-dehors de l’espace-f. Dans ce cas, l'algorithme essaie de calculer un nouvel espace-f en initialisant le RdpFiltré à l'état courant du jeu. Si un état final est atteignable à partir de l'état courant, l'algorithme traite cette action comme dans le cas 2.3. Sinon, l'algorithme détermine si le nouvel état est plus proche d'un état final du niveau que l'état qui le précède (l’étiquette générée est alors « Rapprochement »), plus éloigné (l’étiquette générée est « Eloignement ») ou équidistant (l’étiquette générée est « Stagnation »).

5.1.3. Cas 3 - actions manquantes lorsque le jeu est terminé

Si la dernière action de l'apprenant ne lui permet pas d'atteindre un état final du jeu, l'algorithme recherche le dernier état dans l’espace-f atteint par l'apprenant et calcule le chemin le plus court pour atteindre la fin du niveau à partir de cet état. Ensuite, l'algorithme affecte aux actions de ce chemin l’étiquette « Manquante ».

5.2. Calcul du Score

L'algorithme d’étiquetage présenté ci-dessus produit 16 étiquettes pédagogiques. Nous associons un coefficient pour chaque étiquette afin d'être en mesure de proposer un score (voir tableau 1). Ce score permettra, dans la phase d’expérimentation, de comparer l’évaluation produite par l’algorithme d’étiquetage avec les données des enseignants.

Tout d'abord, nous définissons comme étiquettes positives celles qui garantissent une progression vers un état final. Nous définissons les coefficients associés à ces étiquettes dans l’intervalle ]0 ;1]. Pour cette classe, nous retenons les étiquettes suivantes : « Correcte » dénote un comportement satisfaisant par rapport à la solution des experts (coef=1) ; « Equivalente » est similaire à une action « Correcte », mais fait référence à une action non-experte (d'où un coefficient plus bas : 0,8) ; « Progression » signifie que l’apprenant suit un processus de résolution non-expert mais se rapproche de la solution (coef=0,6) ; et « Rapprochement » est associée au plus petit coefficient positif, car cela arrive lorsque l'apprenant se déplace en dehors de l’espace-f (coef=0,4).

Etiquettespositives	Coef.	Etiquettes négatives	Coef.
Correcte	1	Inutile	-0,1
Equivalente	0,8	Eloignement	-0,2
Progression	0,6	Manquante	-0,3
Rapprochement	0,4	Erronée	-0,5

Ensuite, nous définissons comme étiquettes négatives, celles qui représentent un écart certain par rapport à la solution des experts. Afin de donner plus de poids aux étiquettes positives dans le calcul du score et de moins pénaliser les essais-erreurs, nous définissons les coefficients négatifs dans l'intervalle [-0,5 ; 0[. Pour cette classe, nous retenons les étiquettes suivantes :

• « Manquante » apparaît quand les apprenants abandonnent le niveau, nous choisissons de pondérer fortement cette étiquette pour dégrader le score des étudiants dans le cas d'un abandon (coef=-0,3) ;

• « Inutile » ne caractérise pas une erreur majeure, elle a donc une influence mineure sur le score (coef=-0,1).

L’étalonnage de ces coefficients a été stabilisé après quelques itérations, avec comme noyau structurant des écarts relatifs similaires entre étiquettes opposées (Correcte/Rapprochement vs Erronée/Éloignement).

Finalement, les étiquettes restantes (Non-optimale, Rattrapage, Retour arrière, Stagnation, Prématurées, Tardives, Régression et Non synchronisée) sont classées comme étiquettes neutres. Même si leurs coefficients sont mis à 0, elles vont contribuer au calcul du score en augmentant la taille de la trace, dégradant ainsi le score de l’apprenant.

Dans l'expérimentation que nous avons menée, le score d'une trace d'apprenant a été calculé par la formule (1) et est défini dans l’intervalle [-0,5 ; 1]. Pour une trace, nous notons L = {l₁, l₂, ..., l₁₆} l'ensemble incluant le nombre de chaque sorte d’étiquette et C = {c₁, c₂, ..., c₁₆} l'ensemble définissant le coefficient de chaque sorte d’étiquette.

Naturellement, la pondération des étiquettes et la méthode de calcul de score peuvent être adaptées en fonction des besoins, des objectifs et des pratiques pédagogiques des enseignants.

6. Etude expérimentale

L'architecture globale, incluant la génération assistée des réseaux de Petri ainsi que l’analyse et l’étiquetage des actions d’un joueur, a été évaluée sur un prototype de jeu sérieux appelé « Les Cristaux d'Ehere », conçu pour enseigner les concepts de la physique de l’eau à des élèves de 5^ème au collège. L'objectif pour chaque niveau est de résoudre des problèmes mettant en jeu des compétences relatives à la compréhension de processus de changements d'états de l'eau. Les apprenants doivent déplacer un avatar pour interagir avec des objets du jeu et atteindre une solution mettant en œuvre des compétences en physique. Tous les niveaux du jeu (18) ont été conçus en suivant la méthode que nous avons présentée dans cet article.

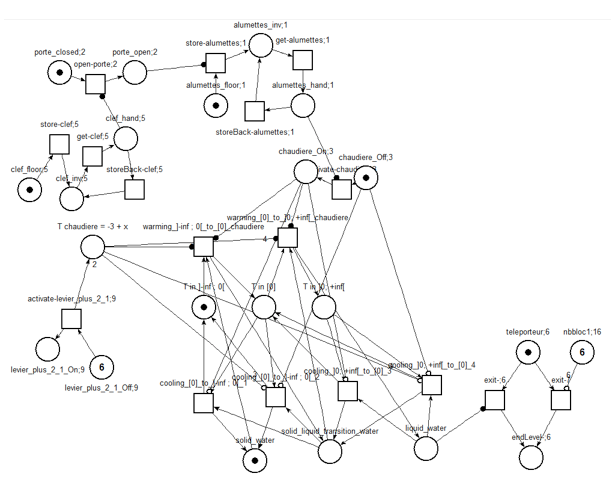
Figure 8 • Réseau de Petri filtré (construit automatiquement) du niveau « Le mur de glace »

Nous présentons ici les résultats concernant deux niveaux : « Le thermomètre » et « Le mur de glace ». Dans le premier, « Le thermomètre », l'apprenant travaille sur la compétence « Lire la température précisément sur un thermomètre analogique » et dans le second, « Le mur de glace », il travaille des compétences relatives à la compréhension de la fonte de l'eau à l'état solide. Les figures 7 et 8 montrent respectivement une copie d'écran et le réseau de Petri filtré (avec l’aide de la trace d’un seul expert) du niveau « Le mur de glace ». L’analyse du graphe d’accessibilité complet de ce dernier niveau s’élève à 3 780 états de jeu reliés par 24 120 liens, réduits à 97 états (dont 20 états représentant des états finaux du jeu) et 326 liens pour sa version filtrée avec la trace experte.

6.1. Protocole expérimental

L'objectif de cette expérimentation est de déterminer si les étiquettes et le score calculé par l'algorithme donnent une idée satisfaisante du comportement d'un apprenant et sont cohérents avec les retours (scores) proposés par les enseignants.

Nous avons mené une expérimentation de nature qualitative avec neuf élèves et quatre enseignants de physique au collège. Un protocole expérimental a été suivi afin d’analyser l'efficacité de l'algorithme d'étiquetage auprès des enseignants. Tout d'abord, nous avons filmé les écrans des élèves pendant les sessions de jeu. Ensuite, nous avons présenté les niveaux du jeu aux enseignants.

Pour évaluer la qualité des étiquettes proposées, nous avons demandé à trois enseignants sur les quatre de visualiser les vidéos des apprenants résolvant les niveaux « Le thermomètre » et « Le mur de glace ». Nous leur avons demandé d'évaluer le comportement de trois apprenants avec un score global sur une échelle de 1 à 3 : 1 pour un élève qui a échoué ou rencontré de sérieuses difficultés à résoudre le niveau, 2 pour un élève qui rencontre quelques difficultés et 3 pour un élève qui a montré une bonne compréhension des concepts du domaine sous-jacents à la résolution du niveau. Nous avons limité l’évaluation à trois catégories pour aider les enseignants à classer les élèves. En effet, n’ayant à leur disposition que les vidéos des sessions de jeu, ils éprouvaient des difficultés pour positionner les élèves sur des échelles plus fines. Le classement en trois niveaux était donc le meilleur compromis permettant aux enseignants d’avoir confiance en leur classification. Ensuite, nous avons fourni la liste des étiquettes pédagogiques et leur signification. Nous avons demandé à ces mêmes enseignants d'étiqueter les actions des élèves manuellement en utilisant la liste des étiquettes. Une fois qu'ils avaient étiqueté les actions des trois élèves, nous leur avons présenté les étiquettes générées par l'algorithme d’étiquetage. Enfin, nous avons soumis aux enseignants un questionnaire afin d'évaluer la qualité des étiquettes générées automatiquement.

D’autre part, nous avons demandé au quatrième enseignant de visionner les vidéos de tous les apprenants pendant les deux niveaux et d'évaluer le comportement des apprenants avec la même échelle de score que celle des trois autres enseignants, mais sans qu’il ait connaissance des étiquettes. Notre objectif était de vérifier si le processus d’étiquetage pouvait influencer la notation des enseignants. Enfin, nous avons comparé le score calculé automatiquement par LaaLys V2 aux notes données par cet enseignant.

6.2. Résultats et discussion

6.2.1. L'avis des enseignants sur les résultats de l'algorithme d’étiquetage

Les trois enseignants ont été capables d'étiqueter les traces de chacun des trois élèves entre 3 et 10 minutes, en fonction de la longueur de la trace. L’interview de ces enseignants a montré qu’ils considèrent unanimement que les étiquettes ont un sens pédagogique et apportent une bonne compréhension du comportement des élèves.

Quand nous avons comparé l'étiquetage automatique à ceux réalisés manuellement par les enseignants, nous avons noté une grande similarité. Néanmoins, les enseignants ont souvent confondu les étiquettes « Rattrapage » et « Retour arrière ». En effet, ces deux étiquettes sont très similaires même si elles restent sémantiquement différentes et nécessiteraient donc plus d'explication auprès des enseignants. Aussi, un des enseignants n'a pas compris la signification de l'étiquette « Non synchronisée » et par conséquent, ne l'a pas utilisée. Après discussion avec cet enseignant, nous pensons que cette étiquette peut être assimilée à l'étiquette « Prématurée » car le fait qu'une action a été disponible dans le passé n'est pas important et que la caractéristique la plus utile pour l'enseignant est surtout de savoir si une action va être disponible dans le futur pour l’apprenant.

Les trois enseignants ont estimé que les étiquettes choisies par l'algorithme étaient plus précises que leurs propres choix et que cela représente une économie en temps substantielle, en comparaison avec la production et le visionnage des vidéos. Ils proposent dans le même esprit d'extraire automatiquement des motifs plus abstraits de regroupement d'étiquettes : par exemple, la détection répétée dans une trace de plusieurs actions « Prématurée » ou « Tardive » pourraient montrer qu'un apprenant ne comprend pas les contraintes temporelles du processus métier simulé par le jeu. Cela permettrait un retour d’un niveau d’abstraction plus adapté pour les enseignants.

Finalement, nous avons comparé les scores donnés par les trois premiers enseignants et ceux donnés par le quatrième enseignant (nous ne considérons ici que les trois étudiants ayant été évalués par tous les enseignants). Le coefficient de Kappa (k=0,9) montre que l’activité d’étiqueter les traces n’influence pas la notation des enseignants puisque les quatre enseignants ont noté les élèves de manière très proche.

6.2.2. Comparaison des scores de Laalys V2 avec les notes données par le 4ème enseignant

Le tableau 2 montre les données expérimentales sur les niveaux « Le thermomètre » et « Le mur de glace ». Pour ces deux niveaux, nous présentons les données pour les neuf élèves (S1 à S9). La première ligne donne pour chaque élève le score automatique fourni par l'algorithme (rapporté et discrétisé sur l'ensemble des valeurs [1 ; 2 ; 3]) et la deuxième ligne le score attribué par le quatrième enseignant. La dernière ligne donne la longueur de la trace.

Tableau 2 • Comparaison des scores de chaque élève pour les niveaux « Le thermomètre » et « Le mur de glace »

	Le thermomètre									Le mur de glace
	S1	S2	S3	S4	S5	S6	S7	S8	S9	S1	S2	S3	S4	S5	S6	S7	S8	S9
Score de Laalys V2	2	1	1	3	1	1	1	1	1	3	1	2	3	1	3	1	3	1
Score de l’enseignant	2	1	1	3	1	3	1	2	1	3	2	2	3	1	2	1	3	1

Longueur de la trace	8	27	18	6	23	18	33	35	32	9	22	13	13	20	12	13	9	42

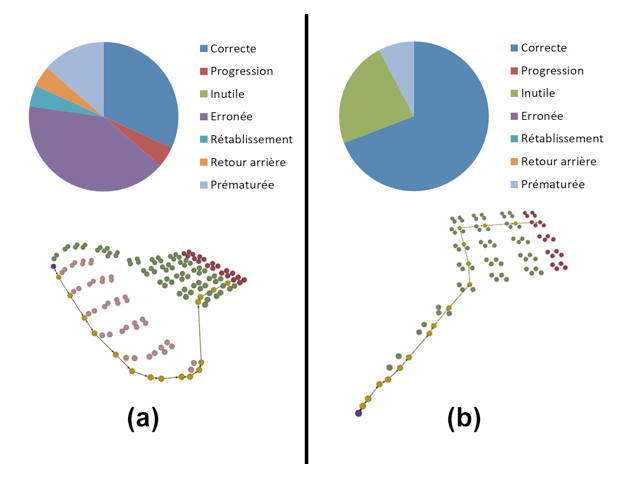
La comparaison des scores de l’enseignant et des scores calculés par Laalys V2 donne un coefficient de Kappa de 0,64 et permet de conclure à un accord fort entre ces différents scores. Toutefois, nous notons une divergence entre les scores pour les deux élèves S6 et S8 dans le niveau « Le thermomètre », ainsi qu’entre les scores pour les deux élèves S2 et S6 dans le niveau « Le mur de glace », ce que nous explicitons ci-dessous.

Thermomètre S6 : ce cas est le plus grand écart entre le score donné par l’enseignant (3) et le score calculé automatiquement (1). L’enseignant a noté que l'élève a tâtonné pour atteindre la solution, a essayé un grand nombre de choses et a vérifié la température après chaque action. L'algorithme a détecté ce comportement en étiquetant plusieurs actions avec l'étiquette « Stagnation » dans la trace de l'élève, ce qui a dégradé le score automatique de l’élève. Cependant, l’enseignant a été indulgent en notant l’élève S6 car il avait remarqué que le tâtonnement de l’élève était dû à un bug dans le jeu (la loupe facilitant la lecture de la température sur le thermomètre ne s’affichait pas) et non à un manque de compétence chez l’élève S6.

Thermomètre S8 : l’enseignant note que cet élève actionne les leviers contrôlant la température sans tester systématiquement la sortie du niveau. Selon l’enseignant, c'est un bon comportement mais le moteur du jeu ne trace pas l’information de tester la sortie. Si c'était le cas, le score calculé aurait été meilleur que celui des autres élèves qui n’avaient pas ce comportement.

Le mur de glace S2 : l’enseignant justifie sa note avec les mêmes explications que pour l'élève S5 mais n'a pourtant pas donné la même note. Du point de vue de l'analyse automatique, les deux traces sont très similaires et donc le score l'est aussi. Cela semble montrer un résultat plus cohérent que l'évaluation de l'enseignant.

Le mur de glace S6 : l’enseignant a commenté le comportement de l'élève comme celui des élèves qui ont obtenu la note 3 (S1, S4 et S8). Or la note est différente (2). Il n'a pas expliqué les différences entre ces élèves. Là encore l'analyse automatique semble plus cohérente.

7. Conclusion et travaux futurs

Le travail présenté dans cet article concerne l'évaluation du comportement des apprenants dans des jeux sérieux avec de grands espaces d’états. Deux contributions sont détaillées : (1) la construction assistée de réseaux de Petri modélisant des entités du jeu et leurs dépendances et (2) l’algorithme d’analyse qui permet d'étiqueter les actions de l'apprenant au moyen d’un ensemble d’étiquettes pédagogiques. Nous avons proposé une méthode que nous avons mise en œuvre pour produire les réseaux de Petri des 18 niveaux du jeu sérieux « Les Cristaux d'Ehère ». L'algorithme d’étiquetage a été expérimenté lors d’une étude qualitative avec neuf élèves et quatre enseignants de collèges. L'évaluation a donné des résultats positifs à la fois sur l'utilité des étiquettes et sur la concordance des scores calculés par le système avec les notes attribuées par les enseignants. Comme évoqué dans la section 6.1, nous avons fait le choix d’une échelle à trois niveaux, car les enseignants avaient des difficultés à justifier leurs notes avec une échelle plus détaillée, sur la seule base de la vidéo. Pour pouvoir affiner leur classement, les enseignants auraient souhaité avoir des données supplémentaires comme les questions posées par les étudiants en cours de jeu. Nous pourrions alors vérifier si ses scores affinés restent homogènes entre enseignants et avec le score généré automatiquement.

Nous avons étendu une recherche initialement conçue pour des jeux de type « études de cas » à des jeux offrant une plus grande liberté d’action au joueur, le jeu « Les Cristaux d’Ehère » pouvant être classé dans la catégorie des jeux d’aventure de type Point And Click. Nous souhaitons poursuivre nos recherches pour généraliser davantage cette approche et permettre de (1) suivre des objets de jeu générés dynamiquement en cours de simulation (donc non inclus dans le réseau de Petri initial) et (2) simplifier la prise en compte des intervalles de validité de l’état d’un objet, par exemple définir qu’une action peut être réalisée si tel objet a sa propriété comprise entre X et Y (actuellement ce mécanisme peut être embarqué dans le réseau de Petri lors de la modélisation mais mériterait d’être défini lors de la phase de résolution experte).

Nous souhaitons également travailler sur une visualisation synthétique permettant aux enseignants d’interpréter plus rapidement les labels pédagogiques. Ces visualisations pourraient être annotées et prendre la forme de diagrammes ou de visualisation abstraite du parcours des apprenants. La figure 9 présente une piste de visualisation pour deux apprenants ayant joué au niveau « Le mur de glace ». Le diagramme en secteur permettrait de proposer aux enseignants une synthèse de l’activité de chaque étudiant afin qu’ils puissent repérer rapidement ceux qui ont eu le plus de difficultés à résoudre un niveau donné. Dans la vue abstraite du processus de résolution, les sphères vertes représentent l’espace-f, la sphère bleue correspond à l’état initial du niveau, les sphères rouges représentent les états finaux et les sphères jaunes les états du jeu parcouru par l’apprenant. Cette vue permettrait aux enseignants d’identifier à quel moment l’élève a quitté l’espace-f, quelles étapes lui ont permis de corriger ses erreurs ou s’il a abandonné le jeu en étant proche de la solution. Ces propositions de visualisation doivent encore être travaillées et évaluées conjointement avec les utilisateurs.

Figure 9 • Piste de visualisations de la trace de deux étudiants pour le niveau « Le mur de glace » pour une interprétation aisée par les enseignants

Ce travail a également permis d'envisager plusieurs nouvelles pistes de recherche : (1) utiliser l’analyse du comportement de l’apprenant et son score pour, par exemple, l’affecter à un groupe de niveau, (2) utiliser les étiquettes afin d'implémenter un retour (feedback) en ligne et adapté à chaque élève, (3) implémenter la propagation des étiquettes dans un modèle cognitif de l’apprenant et (4) comparer les réseaux de Petri (RdpFiltré) construits par filtrage automatique des réseaux complets (RdpComplet) et les réseaux de Petri construits manuellement par les experts.

^1. Bien qu’Unity intègre la notion de composition (les GameObjects sont définis par un ensemble de composants), les composants Unity contiennent à la fois les données et leurs traitements. Unity n’est donc pas une architecture ECS.

À propos des auteurs

Mathieu Muratet est maître de conférences en informatique à l'INS HEA (Institut National Supérieur de formation et de recherche pour l'éducation des jeunes Handicapés et les Enseignements Adaptés) et mène ses recherches au sein de l’équipe MOCAH (Modèles et Outils en ingénierie des Connaissances pour l'Apprentissage Humain) du LIP6 (Laboratoire d'Informatique de Paris 6). Il s’intéresse au domaine des jeux sérieux et plus précisément aux problématiques liées à leur conception et au suivi des apprenants en vue de produire des feedbacks adaptatifs.

Adresse : Sorbonne Université, CNRS, INS HEA, Laboratoire d’Informatique de Paris 6, LIP6, F-75005 Paris, France

Amel Yessad est maître de conférences en informatique à Sorbonne Université et mène ses recherches au sein de l’équipe MOCAH (Modèles et Outils en ingénierie des Connaissances pour l'Apprentissage Humain) du LIP6 (Laboratoire d'Informatique de Paris 6). Elle s’intéresse à la représentation et l’extraction automatique de connaissances dans des systèmes informatiques dédiés à la formation et à l’apprentissage humain. Elle applique ses travaux en ingénierie des connaissances au suivi automatique des apprenants, notamment dans les jeux sérieux et l’adaptation des scénarios d’apprentissage à leur profil cognitif.

Adresse : Sorbonne Université, CNRS, Laboratoire d’Informatique de Paris 6, LIP6, F-75005 Paris, France

Thibault Carron est enseignant-chercheur en informatique, habilité à diriger des recherches depuis 2011 à l'université Savoie Mont Blanc. Il est membre de l'équipe MOCAH du LIP6 (Sorbonne Université). Il a obtenu sa thèse en 2001 à l'école nationale supérieure des Mines de Saint-Etienne. Il s'intéresse à l'observation de l'activité collaborative et plus particulièrement aux jeux sérieux.

Adresse : Sorbonne Université, CNRS, Université Savoie Mont Blanc, Laboratoire d’Informatique de Paris 6, LIP6, F-75005 Paris, France

Arthur Ramolet est diplômé de l’université Pierre et Marie Curie et titulaire d’un Master en informatique (spécialité : ANDROIDE - AgeNts Distribues, Robotique, Recherche Opérationnelle, Interaction, DEcision). Il a mené son stage de Master au sein de l’équipe MOCAH (Modèles et Outils en ingénierie des Connaissances pour l'Apprentissage Humain) du LIP6 (Laboratoire d'Informatique de Paris 6).

Adresse : Sorbonne Université, CNRS, Laboratoire d’Informatique de Paris 6, LIP6, F-75005 Paris, France

REFERENCES

Angeli, C. et Valanides, N. (2013). Using educational data mining methods to assess field-dependent and field-independent learners’ complex problem solving. Educational Technology Research and Development, 61(3), 521-548.

Araújo, M. et Roque L. (2009). Modeling Games with Petri Nets. DiGRA Conference.

Azevedo, R., Harley, J., Trevors, G., Duffy, M., Feyzi-Behnagh, R., Bouchet, F. et Landis, R. (2013). Using trace data to examine the complex roles of cognitive, metacognitive, and emotional self-regulatory processes during learning with multi-agent systems. Dans R. Azevedo et V. Aleven (dir.), International handbook of metacognition and learning technologies (p. 427-449). Springer.

Baradwaj, B. K. et Pal, S. (2012). Mining educational data to analyze students’ performance. IJACSA, 2(6), 63-69.

Bilas, S. (2002). A data-driven game object system. Dans Game Developers Conference Proceedings.

del Blanco, A., Torrente, J., Marchiori, E. J., Martínez-Ortiz, I., Moreno-Ger, P. et Fernández-Manjón, B. (2010). Easing assessment of game-based learning with e-adventure and lams. Dans Proceedings of the Second ACM International Workshop on Multimedia Technologies for Distance Leaning (MTDL’10) (p. 25-30). New York, NY : ACM.

Busi, N. (2002). Analysis issues in Petri nets with inhibitor arcs. In Theoretical Computer Science, 275(1-2), 127-177.

Capdevila, B. (2013). Serious game architecture and design: modular component-based data-driven entity system framework to support systemic modeling and design in agile serious game developments (thèse de doctorat non publiée). Université Pierre et Marie Curie, Paris, France.

Gee, J.P. (2007). What Video Games Have to Teach Us About Learning and Literacy (2nd ed.). New York, NY : Palgrave Macmillan.

Harpstead, E., MacLellan, C. J., Koedinger, K. R., Aleven, V., Dow, S. P. et Myers, B. A. (2013). Investigating the solution space of an open-ended educational game using conceptual feature extraction. Dans Proceedings of the 6th International Conference on Educational Data Mining (p. 51-58). International Educational Data Mining Society.

Kosba, E., Dimitrova, V. et Boyle, R (2007). Adaptive feedback generation to support teachers in web-based distance education. User Modeling and User-Adapted Interaction, 17(4), 379-413.

Medler, B., John, M. et Lane, J. (2011). Data cracker: Developing a visual game analytic tool for analyzing online gameplay. Dans Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI ’11) (p. 2365-2374). New York, NY : ACM.

Peterson, J. L. (1981). Petri Net Theory and the Modeling of Systems. Reading, MA : Prentice Hall.

Thomas, P., Yessad, A. et Labat, J.-M. (2011). Petri nets and ontologies: Tools for the "learning player" assessment in serious games. Dans Proceedings of International Conference on Advanced Learning Technologies (ICALT) (p. 415-419).

Thomas, P., Labat, J.-M., Muratet, M. et Yessad, A. (2012). How to evaluate competencies in game-based learning systems automatically? Dans Proceedings of International Conference on Intelligent Tutoring Systems (ITS 2012) (p. 168-173). Berlin, Allemagne : Springer.

Wallner, G. et Kriglstein, S. (2014). Technical section: Plato: A visual analytics system for gameplay data. Computers and Graphics, 38, 341-356.

Yessad, A., Thomas, P., Capdevila, B. et Labat, J.-M. (2010). Using the petri nets for the learner assessment in serious games. Dans Proceedings of International Conference on Web-Based Learning (ICWL) (p. 339-348).

Young, H. P. (2009). Learning by trial and error. Games and economic behavior, 65(2), 626-643.

¹ Un marquage A = (A₁,..., A_n) englobe un marquage B = (B₁,..., B_n) si quel que soit j, j entre 1 et n, A_j ≥ B_jet il existe au moins un i tel que A_i > B_i.

² Bien que Unity intègre la notion de composition (les GameObjects sont définis par un ensemble de composants), les composants Unity contiennent à la fois les données et leurs traitements. Unity n’est donc pas une architecture ECS.