Sommaire

Rechercher

• auteur
• année
• titre
• résumé
• abstract
• rubrique

Contact : infos@sticef.org

Motivation, comportement dans le jeu et expérience de jeu : une relation aux multiples facettes

Denise SUTTER WIDMER, Nicolas SZILAS (TECFA – FPSE, Université de Genève)

	RÉSUMÉ : Nous avons développé un jeu vidéo pour l’apprentissage de l’algèbre élémentaire, à partir duquel nous étudions comment la motivation à apprendre et à s’engager dans l’activité est liée à la qualité de l’expérience et à l’aisance dans le jeu. Nous avons mis en évidence différents profils d’élèves à partir d’une méthode de classification. Nous montrons que certains joueurs-apprenants sont orientés plutôt jeu, d’autres plutôt contenu, et certains d’entre eux ne sont intéressés de prime abord ni par l’un ni par l’autre. Ces profils correspondent au départ du jeu à des attentes et motivations diverses qui vont en partie déterminer le niveau d’engagement des joueurs-apprenants dans l’activité du jeu et dans l’apprentissage. Il apparaît que si les attentes d’un des profils ne sont pas satisfaites, le niveau d’engagement et les performances dans le jeu vont s’en ressentir négativement. MOTS CLÉS : Jeu sérieux, motivation, engagement, intérêt, flow, expérience de jeu.
Serious game, motivation, engagement, interest, flow, gameplay experience
	ABSTRACT : We developed a video game in Algebra to investigate how motivation to learn and to engage in a learning activity relates to the experiential qualities reported by learners and in-game behavior. We brought out different profiles of students by using a clustering method. We show that some learners are more oriented towards the game, others are more interested by the learning content, and some are neither interested by one nor by the other. Those profiles correspond to different types of expectations and motivations that will determine the level of engagement in the game activity and in the learning. Unfilled expectation was found to negatively impact engagement and performances in the game. KEYWORDS : Serious game, motivation, engagement, interest, flow, gameplay experience

• 1. Introduction
• 2. Cadre théorique
• 3. Méthode
• 4. Résultats
• 5. Discussion
• 6. Conclusion
• 7. Remerciements
• BIBLIOGRAPHIE

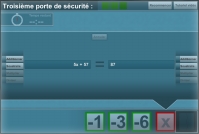
1. Introduction

Les mathématiques et notamment l’algèbre élémentaire posent difficulté à nombre d’adolescents. L’algèbre est abordée dans le cadre de l’enseignement secondaire à un âge où la motivation intrinsèque à apprendre est en général plus faible qu’au niveau primaire. Les adolescents doutent plus volontiers de la valeur du travail scolaire et de leurs compétences à réussir. Leurs besoins – tâches davantage centrées sur l’élève et qui ont du sens pour lui, plus de choix et d’autonomie, moins d’accent sur les notes et les évaluations – sont en décalage avec leur nouveau contexte scolaire (Rathunde et Csikszentmihalyi, 2005). Souvent récalcitrants à entrer dans les apprentissages en raison d’échecs répétés et d’un faible sentiment de compétence, les élèves en difficulté, notamment en mathématiques, sont en général moins motivés à s’investir dans des tâches relevant de cette discipline (Pelgrims, 2009).

Concevoir un environnement motivant et engageant pour l'apprentissage en mathématiques, tel qu’un jeu sérieux, peut se révéler particulièrement pertinent dans de telles circonstances, d’autant plus lorsque l’on s’adresse à une population d’adolescents dont une partie est en butte à des difficultés scolaires. On connaît le succès planétaire des jeux vidéo en termes économiques mais aussi en tant que phénomène culturel (Barr et al., 2007). L’engouement pour les jeux vidéo est lié étroitement au sentiment de plaisir qu’éprouvent les joueurs lorsqu’ils jouent. Les jeux sont considérés comme étant intrinsèquement motivants. Dans cette perspective, un jeu sérieux peut représenter un moyen de récupérer au profit de l’apprentissage la capacité des jeux vidéo à engager fortement les joueurs.

Par jeu sérieux, nous entendons un jeu dont la finalité première n’est pas le simple divertissement mais la formation et l’apprentissage, en référence à la définition de Michael et Chen (Michael et Chen, 2006, p. 17) : « A serious game is a game in which education (in its various forms) is the primary goal, rather than entertainment ». Plus spécifiquement, nous nous intéressons aux jeux qui ont été conçus avec l’intention d’amener les apprenants à construire des connaissances en lien avec des objectifs pédagogiques prédéfinis et qui peuvent être évalués.

Les jeux sérieux combinent deux dimensions (jeu et contenu d’apprentissage) pour lesquelles les apprenants-joueurs ne témoignent pas forcément le même intérêt, ni n’accordent la même valeur ; le sentiment de compétence n’est pas nécessairement identique sur les deux plans. Les défenseurs des jeux sérieux postulent que l’engouement pour les jeux et la capacité d’engagement des jeux vont profiter à l’apprentissage (Malone, 1981), (Mitchell et Savill-Smith, 2004). Qu’en est-il réellement ? Est-ce que des élèves qui ont un intérêt pour le jeu mais qui se sentent peu compétents par rapport au contenu mathématique feraient preuve d’une plus grande persévérance et fourniraient plus d’efforts dans un jeu sérieux que dans des tâches scolaires traditionnelles ? Et inversement, est-ce qu’un intérêt modéré pour le jeu est nécessairement un frein à l’engagement lorsque le contenu d’apprentissage est apprécié et valorisé ?

L’objectif de cette étude est d’identifier différents profils motivationnels d’élèves établis sur la base de caractéristiques individuelles présentes en amont du jeu. Nous cherchons à déterminer dans quelle mesure ces profils peuvent être mis en relation avec certains comportements du joueur, avec l’expérience de jeu telle qu’elle est rapportée par les apprenants à l’issue du jeu, et avec le sentiment d’avoir acquis de nouvelles connaissances. La démarche suivie est de type exploratoire, nous ne formulons pas d’hypothèses a priori. Par ailleurs, nous n’évaluons pas, dans le cadre de cette contribution, les connaissances mathématiques construites à travers l’utilisation du jeu au regard des différents profils motivationnels et ne menons pas d’analyse didactique des données récoltées durant les sessions de jeu.

Dans une première partie, nous abordons différentes notions théoriques en lien avec notre objectif de recherche. Nous évoquons les questions de motivation, d’engagement et d’immersion dans un jeu ainsi que la notion de flow qui permet d’approcher l’expérience subjective des joueurs. Nous définissons aussi ce que nous entendons, dans cette étude, par la notion de comportement du joueur. A l’issue du cadre théorique sont exposées nos différentes questions de recherche.

Dans une deuxième partie, nous présentons Algebra Mystery, un jeu consacré à la résolution d’équations et à la mise en équation, qui a été conçu et développé dans le cadre de cette recherche. Nous introduisons le contenu d’apprentissage et expliquons les fondements de la conception du jeu au niveau mathématique ainsi que les interactions attendues entre les apprenants et le système du jeu en vue de la construction de nouvelles connaissances. Nous décrivons aussi le contexte de l’expérimentation qui a été menée ainsi que les données récoltées qui ont servi à répondre à nos questions de recherche. Nous précisons quels indicateurs ont été retenus pour évaluer le comportement des joueurs. Dans la troisième partie, nous rendons compte des résultats de nos analyses de données. A travers celles-ci, différents profils de joueurs sont mis en évidence en fonction des motivations et attentes au départ des joueurs apprenants ; ces profils sont caractérisés en fonction de comportements dans le jeu et de la qualité d’expérience du jeu.

Dans la dernière partie, nous discutons nos résultats sur les différents profils à la lumière d’éléments issus de la théorie et de nos questions de recherche. Nous élargissons également la discussion à un niveau plus général pour en tirer des conclusions qui pourraient s’avérer utiles pour la conception d’autres jeux sérieux.

2. Cadre théorique

2.1. Aspects motivationnels

De nombreuses théories de la motivation en contexte scolaire ont été proposées et développées depuis plusieurs décennies. Elles portent sur les facteurs individuels et/ou contextuels qui expliquent les choix et décisions des élèves, leurs intentions d’actions, leur engagement dans une tâche, leur persévérance face aux obstacles rencontrés et les émotions ressenties (Pelgrims et Cèbe, 2010). Dans les recherches en psychologie de l’éducation, la motivation à s’engager dans une tâche est perçue aujourd’hui, non plus comme le simple produit mécanique de facteurs internes et externes à l’individu, mais comme dépendant essentiellement des représentations mentales que l’apprenant s’est forgées dans la situation d’apprentissage (Bourgeois, 2011). Ces représentations, dites motivationnelles, sont considérées comme le fruit d’une interaction entre des facteurs internes, propres à l’individu, et des facteurs externes, liés au contexte et à la situation d’apprentissage.

Parmi les facteurs individuels, les facteurs affectifs, tels que le sentiment de compétence, l’estime de soi, l’intérêt et l’utilité des savoirs scolaires, ont fait l’objet de nombreux travaux, notamment par rapport aux élèves en difficulté d’apprentissage (Pelgrims et Cèbe, 2010). Eccles et Wigfield, dans leur théorie de l’expectancy-value (Eccles et Wigfield, 2002), estiment que la valeur accordée à la tâche d’apprentissage et la perception de ses chances de réussite sont les deux prédicteurs les plus importants de la motivation à apprendre chez l’élève. A ces deux composantes viennent s’ajouter chez Viau (Viau, 1998) la contrôlabilité du déroulement et des conséquences de l'activité d’apprentissage. Dans ces différentes approches, l'engagement d'un sujet dans une activité d’apprentissage est donc déterminé par la représentation qu’il a de la situation et de lui-même.

Dans le domaine des mathématiques, la perception qu’ont les élèves, notamment ceux en difficulté scolaire, de leurs compétences va déterminer en grande partie la formation de leur intention à se lancer dans une activité en mathématiques, ainsi que leur engagement et leur persévérance dans celle-ci (Pelgrims et Cèbe, 2010). Souvent en proie à des croyances de type « impuissance acquise », ces élèves attribuent, en raison d’échecs répétés, leurs réussites et échecs à des causes incontrôlables, dissociées de leurs propres actions (Linnenbrink et Pintrich, 2003). S’intéressant à l’attitude des élèves envers cette discipline, Tapia, Marsh et George (Tapia et al., 2004) relèvent que la recherche s’est surtout focalisée, pour les apprenants ayant des mauvais résultats en mathématiques, sur l’anxiété éprouvée par ces derniers. L’anxiété engendrerait une attitude d’évitement vis-à-vis des mathématiques avec pour conséquence une moindre maîtrise des connaissances procédurales et stratégiques et donc à terme une moindre compétence dans cette discipline. D’autres facteurs que l’anxiété et le sentiment d’efficacité personnelle des élèves semblent également jouer un rôle dans les performances en mathématiques, comme la valeur attribuée aux mathématiques dans la vie actuelle et dans le futur, le plaisir de faire des mathématiques et de suivre des cours de mathématiques, l’intérêt pour cette discipline ainsi que l’envie de poursuivre des études en mathématiques.

Choisir le jeu comme un environnement d’apprentissage se justifie pour nombre d’auteurs par le plaisir que procure le jeu. Le concept de motivation intrinsèque est au cœur de l'intérêt de l'utilisation des jeux numériques pour l'apprentissage. Le jeu est essentiellement autotélique (Salen et Zimmerman, 2004) : les joueurs jouent pour le plaisir de jouer, pour la stimulation intrinsèque qu'apporte le jeu. Un jeu bien conçu, que l’on estime réussi, est, par définition, intrinsèquement motivant. La motivation intrinsèque est définie comme le fait qu’une activité est engageante parce qu’elle est satisfaisante et gratifiante en tant que telle et non parce qu’une récompense est promise en cas de réussite (Csikszentmihalyi et Nakamura, 1989). Cette notion renvoie à la perception qu’ont les individus d’une activité. Elle implique que l’activité ou la tâche sont perçues comme étant intéressantes et plaisantes (rewarding) en soi (Ryan et Deci, 2009). La motivation extrinsèque, en revanche, fait référence à une motivation qui incite à s’engager dans une activité en tant que moyen pour atteindre une fin (Schunk et al., 2014).

La motivation intrinsèque intéresse les chercheurs dans la mesure où l’on suppose que les individus font plus d’effort pour apprendre lorsque l’activité est en soi source de satisfaction, de bien-être et de plaisir. Pour Whitton (Whitton, 2010), cependant, c’est moins l’amusement qui va être déterminant dans la création de conditions d’apprentissage efficaces dans un jeu que l’engagement de l’apprenant. Garris, Ahlers et Driskell (Garris et al., 2002) caractérisent le comportement des apprenants-joueurs motivés comme étant plus susceptibles de s’engager dans une tâche, d’y consacrer des efforts ; ils persévèrent plus longtemps dans des activités que des apprenants moins motivés abandonnent plus facilement. Ils cherchent aussi plus activement à relever des défis et sont plus enclins à poursuivre une tâche initiée. La motivation intrinsèque devrait promouvoir l’apprentissage et la réussite de manière plus importante que la motivation extrinsèque (Schunk et al., 2014).

Dans leur taxonomie des motivations intrinsèques de l’apprentissage, Malone et Lepper (Malone et Lepper, 1987) ont mis en avant quatre catégories de motivations individuelles qui caractérisent bon nombre de jeux considérés comme intrinsèquement motivants : le défi, la curiosité, le contrôle, et l’imaginaire. Les catégories « défi » et « contrôle » renvoient à la théorie de l’auto-détermination. Pour ces auteurs, des activités sont intrinsèquement motivantes quand elles défient les compétences des apprenants, présentent l’information et les idées en dissonance avec les connaissances et croyances des élèves, ou de manière surprenante ou incongrue, fournissent aux apprenants un sentiment de contrôle sur leurs résultats et, enfin, les invitent dans un monde imaginaire et fictif à travers des simulations et des jeux qui les placent dans des situations hors du monde réel.

Des éléments interpersonnels comme la compétition, la coopération et la reconnaissance sont également évoqués par Malone et Lepper (Malone et Lepper, 1987) comme relevant d’autres formes de motivation intrinsèque. Pour Lazzaro (Lazzaro, 2004), le plaisir de jouer est non seulement lié au défi (hard fun), à la curiosité, à l’imaginaire (easy fun) et au partage d’expériences sociales mais aussi à un état émotionnel altéré caractérisé par des émotions positives. Du point de vue de la conception des jeux sérieux, certains chercheurs avancent que c’est par l’intégration intrinsèque du contenu d’apprentissage et du jeu que la motivation intrinsèque suscitée par le jeu est pleinement exploitée (Habgood et Ainsworth, 2011).

2.2. Engagement, immersion et qualité de l’expérience de jeu (flow)

Dans le monde des jeux vidéo, deux approches peuvent être mises en évidence en lien avec l’engagement : l’engagement y est étudié soit en tant qu’état émotionnel et cognitif soit en tant que processus (Molinari et al., 2016). En tant que processus, l’engagement correspond à différents niveaux d’immersion ou d’implication dans le jeu qui peuvent évoluer en fonction des activités et des tâches menées (Brockmyer et al., 2009), (Jennett et al., 2008). L’expérience psychologique d’engagement n’est donc pas forcément optimale comme l’entend la notion de flow mais peut fluctuer dans le temps. L’engagement est alors perçu comme une succession de points d’engagement, de désengagement et de réengagement (O’Brien et Toms, 2008). Pour (Brockmyer et al., 2009) l’engagement est un indicateur générique de l’implication dans le jeu qui évolue selon une échelle dont les différents échelons sont l’immersion (niveau le plus bas), la présence, le flow et l’absorption psychologique (engagement total). Le flow est, dans cette approche, une forme particulièrement poussée d’implication dans le jeu.

L’immersion dans les jeux et l’engagement sont des notions étroitement liées. L’immersion fait partie de l’expérience des joueurs et résulte de l’interaction avec l’environnement du jeu ; elle fait référence au degré d’implication dans le jeu. Brown et Cairns (Brown et Cairns, 2004), sur la base d’entretiens avec des joueurs, ont dégagé trois niveaux d’immersion et ont identifié un certain nombre de barrières (par ex. les préférences des joueurs, les caractéristiques du jeu) qui peuvent limiter le degré d’immersion dans un environnement de jeu. Le premier niveau d’immersion correspond à l’engagement ; il est une condition préliminaire à toute forme d’immersion. Pour qu’il y ait engagement, le joueur doit être prêt à investir du temps, de l’effort et de l’attention pour apprendre le jeu et pour parvenir à maîtriser les principales fonctionnalités du jeu. Cela présuppose au départ qu’il apprécie le type de jeu proposé ou du moins qu’il est intéressé à s’y investir si celui-ci ne lui est pas familier.

Le deuxième niveau d’immersion est intitulé engouement (engrossment). Il est étroitement lié à la conception du jeu ; il se produit lorsque les émotions du joueur sont influencées par le jeu en raison de certaines de ses caractéristiques (scénario, graphisme, tâches captivantes). Les joueurs deviennent moins conscients d’eux-mêmes et de leur environnement. Au troisième niveau, le joueur est en totale immersion : il est complètement présent dans le jeu, se sent détaché de la réalité à tel point que seul le jeu est alors important à ses yeux. Le jeu mobilise toutes ses ressources attentionnelles et ses émotions sont directement affectées par celui-ci. Pour que ce niveau d’immersion puisse se réaliser, le jeu doit être conçu de manière à ce que le joueur puisse s’identifier avec les situations du jeu (par exemple dans le cadre des jeux de rôle) et que les éléments du jeu participent à la création d’une atmosphère spécifique. Ce dernier niveau d’immersion est rarement atteint.

Pour Gunter, Kenny et Vick (Gunter et al., 2008), l’apprenant-joueur est pleinement immergé dans un jeu sérieux lorsqu’il est complètement engagé et concentré sur les objectifs d'apprentissage et les buts du jeu. Un apprenant-joueur engagé est actif, fournit un effort mental, fait preuve d’attention, de persistance, montre de l’intérêt, vit émotionnellement le jeu, s’investit psychologiquement et intellectuellement. Il ne procède pas systématiquement par essai/erreur et régule ses actions en fonction des feedbacks fournis par le milieu du jeu. L'engagement généré par une immersion totale est à la fois cognitif, physique, psychologique et émotionnel, et conduit ainsi à l'émergence d'un processus cognitif élaboré propice à l’apprentissage.

Dans la perspective de Jennett et al. (Jennett et al., 2008), l’immersion, qui n’est pas définie selon différents niveaux, requiert également de la concentration, mais aussi un sentiment de défi et de contrôle sur le jeu, une implication émotionnelle et une dissociation par rapport au monde environnant. La dissociation temporelle et la perte de conscience de son environnement sont considérées comme des indicateurs d’un engagement élevé. L’immersion n’implique pas forcément le sentiment de présence : on peut se sentir immergé dans un jeu comme Tetris sans avoir le sentiment d’être dans un monde constitué de blocs qui tombent. L’immersion a un lien évident avec la notion de flow (cf. chapitre 3.4). Mais, selon Jennett et al. (2008), l’immersion n’est pas forcément une expérience psychologique optimale, telle qu’elle est définie dans la théorie du flow (Csikszentmihalyi, 1990), bien qu’elle puisse en être un prélude.

La théorie du flow (Csikszentmihalyi, 1990) est une manière d'appréhender la qualité d’expérience de jeu à travers l’expérience subjective du joueur. Le flow, ou l’expérience optimale, fait référence au plaisir qu'éprouve un joueur à s'engager dans une activité de jeu et à y rester (Salen et al., 2009). Il se caractérise par un état psychologique et émotionnel où prédominent les sentiments de joie, d'accomplissement, de compétence. L’expérience optimale n’est pas propre au monde du jeu mais la présence de différents éléments propices à l’émergence du flow (buts clairs, feedbacks immédiats, niveau de difficulté adapté aux compétences des individus et environnement autorisant la conscience aigue des actions à entreprendre) peut contribuer à en faire des environnements de jeu et d’apprentissage engageants pour les apprenants.

Certains éléments permettent d’identifier l’état de flow : une attention entièrement fixée sur l’action en cours, l’exclusion de la conscience des distractions, l’effacement temporaire de la conscience de soi et l’altération de la perception du temps. Dans cet état, caractérisé par une forte immersion dans l’activité en cours, les joueurs se trouvent profondément engagés dans le jeu mais sans que cela engendre d’effort conscient (deep but effortless involvement). Dans la théorie du flow, l’immersion fait donc référence à l'implication extrême du joueur durant le temps du jeu mais aussi aux sentiments très plaisants engendrés par cette situation. Elle a pour effet positif de contribuer à la persévérance du joueur/apprenant dans le jeu malgré les obstacles rencontrés tant que ceux-ci n’apparaissent pas totalement insurmontables. Enfin, le sentiment de contrôle sur ses actions et sur l’interaction avec l’environnement dans lequel l’apprenant se trouve, le besoin de savoir que ses compétences sont adaptées au medium et que celui-ci répond à ses actions, jouent un rôle dans l’émergence du flow dans un environnement d’apprentissage (Esteban-Millat et al., 2013).

Plusieurs auteurs se sont interrogés sur l’effet d’un état de flow intense sur l'acquisition d'un savoir (Egenfeldt-Nielsen, 2005), (Habgood, 2007). En effet, le développement des compétences métacognitives que l’on considère comme essentielles pour un apprentissage efficace (Bransford et al., 2000), est susceptible de souffrir de l'effet d'immersion des jeux en empêchant la prise de recul nécessaire à l'émergence d'une réflexion sur les apprentissages en cours, et ce d'autant plus lorsque les éléments d'apprentissage ne sont pas dissociés de l'expérience de jeu (Szilas et Sutter Widmer, 2009).

L’engagement dans un jeu sérieux peut donc être analysé à travers deux approches : l’examen du comportement de l’apprenant-joueur durant le jeu à travers l’analyse de ses interactions avec le logiciel ; l’expression par l’apprenant-joueur de son expérience de jeu. Nous avons cherché à combiner les deux approches.

2.3. Questions de recherche

Compte tenu des éléments théoriques qui précèdent, nous chercherons à mettre en évidence différents profils motivationnels d’élèves, construits à partir de la valeur accordée au contenu mathématique, au sentiment de compétence de l’apprenant et à son intérêt pour les mathématiques et pour l’activité de jeu proposée.

Notre première question de recherche porte sur le lien entre la qualité de l’expérience du jeu telle qu’elle est rapportée par les apprenants/joueurs après l’utilisation d’un jeu en algèbre élémentaire et le profil motivationnel. Notre deuxième question de recherche a pour objectif de déterminer si, dans le cadre d’un jeu en mathématique, certains profils motivationnels sont associés à un engagement plus marqué des apprenants et à une plus forte immersion dans le jeu. Notre troisième question de recherche s’interroge sur la relation entre l’aisance, versus difficulté, des apprenants dans le jeu, et leur profil motivationnel.

3. Méthode

3.1. Participants

Les participants étaient des élèves âgés de 13-15 ans, au nombre de 94, issus de 7 classes différentes d’un établissement de l’enseignement secondaire genevois (Suisse), situé dans un quartier où règne une certaine mixité sociale. Les filles, au total de 52, étaient légèrement surreprésentées par rapport aux garçons (42). Les élèves provenaient aussi bien de sections dites pré-gymnasiales (« latines », « scientifiques » ou « langues modernes »), que de sections non pré-gymnasiales, regroupant des élèves soit un peu plus faibles (section Langues vivantes et communication) voire nettement plus faibles (section Communication et technologie). Ceux des sections les plus fortes (57 au total) étaient en 10^ème année tandis que les élèves des sections dites moyennes (24 élèves) et faibles (13 élèves) étaient déjà en 11^ème, autrement dit en dernière année de la scolarité obligatoire. Selon les enseignants consultés, le niveau de difficulté des problèmes mathématiques abordés dans le jeu était adapté aussi bien à des élèves de 10^ème en section pré-gymnasiale qui se destinent à des études supérieures, qu’à des élèves de 11^ème engagés dans des sections moins fortes. Pour les élèves de 10^ème année la mise en équation de problèmes constituait un chapitre nouveau dans le champ des équations alors que les élèves de 11^ème avaient déjà abordé la mise en équation de problèmes l’année précédente avec plus ou moins de bonheur.

3.2. Matériel

Le jeu vidéo Algebra Mystery met en scène une intrigue policière dont le dénouement passe par la résolution de problèmes algébriques. Le joueur joue le rôle d’un expert scientifique ; il aide la police à résoudre des énigmes policières en apportant son expertise en mathématiques.

Dans la première partie du jeu, le joueur doit franchir trois portes pour accéder à son laboratoire ; chacune de ces portes s’ouvre grâce à un code secret que le joueur découvre grâce à la résolution d’une équation. Les équations à résoudre, générées automatiquement par le système, doivent être simplifiées en appliquant les règles d’équivalence et leur complexité augmente à chaque porte (équations de type x + a = b, puis ax = b et finalement ax + b = c). Les règles d’équivalence assurent la conservation de l’égalité par addition, soustraction et division (nombre non nul dans les deux derniers cas).

Pour aider les élèves à construire la notion d’équivalence lors de la phase de résolution d’une équation, celle-ci est représentée visuellement par un jeu d’équilibre entre les deux membres d’une équation (Figure 1). Une bonne compréhension du concept d'équivalence est, en effet, essentielle pour réduire une équation. Nombre d'élèves remplacent rapidement les règles de transformation (addition/soustraction du même nombre à chaque membre de l'équation) en règles plus économiques (passage d'un membre de l'autre côté de l'équation en changeant de signe) qui sont souvent sources d'erreurs si le concept d'équivalence n'a pas vraiment été assimilé. Le risque en appliquant les procédures mathématiques sans comprendre les règles qui les sous-tendent est qu’elles perdent leur sens car elles sont alors dissociées des connaissances conceptuelles (Mayer, 2007).

Figure 1 • Représentation de la mécanique du concept d’équivalence

La métaphore visuelle proposée s’apparente au principe de la balance, souvent utilisée dans les manuels scolaires de mathématiques pour introduire la méthode des équations équivalentes. Lorsque le déséquilibre apparaît, le signe « = » en gris se transforme en signe « ≠ », en rouge et reste tel quel tant que le déséquilibre est maintenu. La visualisation de l’équivalence, ou absence d’équivalence, à travers le recours à des couleurs distinctes, attire l’attention de l’élève sur la signification spécifique du signe « = » dans une équation, qui est différent du signe « = » annonçant un résultat (5 + 4 = 9). Le signe « = » traduit ici une relation d’équivalence. La représentation choisie a pour but non seulement de faire appliquer la règle « ce qui est fait d’un côté, doit être fait de l’autre côté » mais aussi d’aider l’apprenant à réaliser que l’égalité d’une équation lors de sa simplification est conservée tant que les mêmes opérations sont effectuées de part et d’autre de l’équation.

Dans la deuxième partie du jeu, qui constitue le cœur du jeu, le joueur doit résoudre, à l’aide d’équations, des problèmes mathématiques qui vont lui permettre d’éclaircir une enquête sur un vol de tableaux. Il s’avère que seules les ficelles servant à emballer et transporter les tableaux ont été retrouvées par la police. Afin de pouvoir identifier les trois tableaux volés, les apprenants doivent calculer les dimensions respectives de ces derniers à partir de données fournies sur les ficelles récupérées et d’informations transmises par des témoins.

Figure 2 • Mise en équation d’un problème à l’aide d’une simulation 3D

Les joueurs commencent par ficeler un paquet 3D (simulation) avec des bouts de ficelle « connues » et « inconnues », qu’ils découpent conformément aux données de l’énigme. La simulation 3D (Figure 2), qui donne une représentation concrète du problème, a pour objectif d’aider les élèves à poser leur équation qu’ils peuvent saisir en parallèle au ficelage ou une fois le paquet complètement ficelé dans une zone dédiée à l’écriture de l’équation. Elle devrait faciliter le passage entre les deux registres de représentation que sont l’énoncé d’un problème, qui relève du langage naturel, et une écriture algébrique, par définition abstraite. La conversion dans un nouveau registre (texte vers l’équation) est une opération cognitive lourde pour les apprenants, d’autant plus difficile à effectuer lorsque les deux registres ont des unités de représentations fort éloignées l’une de l’autre (Duval, 1993), (Duval, 2002). La représentation concrète, qui constitue un passage obligé entre les deux autres représentations, sert à réduire la non congruence entre les unités respectives des deux autres représentations (texte et équation) et à soutenir les opérations mentales requises pour traduire un problème (langage textuel) en équation (écriture algébrique) selon le principe de supplantation (Salomon, 1972), (Vogel et al., 2007). De par sa nature visuelle, concrète et manipulable, la simulation devrait contribuer à la construction d’une représentation mentale interne du problème.

La construction des concepts d’inconnue et de variables se fait donc à travers leur représentation dans différents registres sémiotiques. Le ficelage du paquet peut être défini comme un jeu de correspondances entre différents registres sémiotiques de représentations. Une fois le paquet ficelé, ou en cours de ficelage, l’apprenant saisit l’équation correspondante dans la zone dédiée à cet effet. Une fois l’équation écrite et le paquet ficelé correctement, l’apprenant peut résoudre l’équation. Les apprenants ayant souvent beaucoup de peine à faire le lien entre deux représentations (Ainsworth, 1999), ils ont à leur disposition un bouton de mise en correspondance des deux représentations (bouton Visualiser) qui leur signale par des indices visuels de couleur différente les éléments correspondants (les données s’affichent en vert) ou non correspondants (en orange) dans l’équation et sur le paquet.

Trois problèmes similaires sont soumis aux apprenants pour les amener à comprendre et à exercer la mise en équation (voir exemple Figure 3).

Figure 3 • Données du problème (exemple type)

L’interface est commune aux trois problèmes, mais certains paramètres changent d’un problème à l’autre comme le choix des valeurs inconnues et les relations entre les grandeurs. Les données sont puisées aléatoirement dans une base de données pour chacun des trois problèmes que doit résoudre l’apprenant. Les valeurs sont suffisamment complexes (nombres décimaux) pour que les élèves ne soient pas tentés de calculer la solution de tête par tâtonnement ou par réversion des opérations. Le choix des variables didactiques est essentiel pour rendre le recours à l’algèbre nécessaire et contribuer à donner du sens à son utilisation.

Du point de vue de la conception d’un jeu sérieux, Algebra Mystery a été conçu selon des principes d’intégration intrinsèque du contenu pédagogique et des éléments de jeu (Habgood, 2007), (Szilas et Sutter Widmer, 2009). La progression dans le jeu est ici indissociable de la progression dans les apprentissages, la résolution des problèmes mathématiques étant intégrée dans la fiction et la mécanique du jeu.

3.3. Procédure

Les élèves ont d’abord dû répondre en classe à un questionnaire créé pour l’occasion comportant des items sur le sentiment de compétence en mathématiques, sur la valeur accordée à cette discipline et au jeu dans une perspective d’apprentissage, ainsi que sur leur intérêt pour l’activité proposée. Lors d’une leçon suivante en mathématiques, en salle informatique, les élèves se sont engagés dans une session de jeu d’une durée de 60 minutes, au cours de laquelle ils devaient d’abord résoudre trois équations de difficulté croissante (franchissement des portes) avant de mettre en équation trois problèmes d’ordre géométrique relativement similaires (énigmes des tableaux). Suite au jeu, les participants ont rempli un second questionnaire sur leur perception de l’activité (satisfaction, sentiment d’avoir appris et quelques indicateurs du flow).

Nous précisons que cette étude fait partie d’un projet de recherche plus large, comportant un groupe de contrôle, au cours duquel les compétences des élèves en algèbre furent testées avant et après la session de jeu et où ils furent alloués à deux conditions expérimentales différentes qui ne seront pas détaillées ici (Sutter Widmer, 2017).

3.4. Variables et données

En amont de l’expérience de jeu, les aspects motivationnels des apprenants ont été cernés par neuf items, portant respectivement sur le sentiment de compétence en mathématiques (par ex. « Je suis capable de résoudre des problèmes de maths sans trop de difficultés »), le plaisir éprouvé à faire des mathématiques à l’école (par ex. « J'ai en général du plaisir à faire des maths à l'école »), la valeur accordée aux mathématiques (par ex. « Les maths c’est sans intérêt et ennuyeux ») et aux jeux mathématiques (par ex. « Les jeux mathématiques aident à apprendre les maths »), ainsi que sur leur intérêt pour l’activité proposée (par ex. « Je suis content de faire ce jeu »). Les réponses étaient données selon une échelle de Lickert à 5 points. Plusieurs de ces items proviennent de l’instrument présenté dans (Tapia et al., 2004) pour mesurer l’attitude des élèves envers les mathématiques. Ces auteurs prennent en compte des items qui renvoient au sentiment de compétence, à l’anxiété face aux mathématiques, à la valeur attribuée à cette discipline, au plaisir éprouvé à faire des mathématiques et à la motivation.

Le questionnaire post-jeu, conçu également en utilisant une échelle de Lickert à 5 points, fut distribué immédiatement après la session du jeu. Il compte 21 items qui portent sur des indicateurs d’un état de flow (par ex. « Pendant le jeu, j’ai pensé à d’autres choses sans rapport au jeu »), le sentiment de plaisir ou d’ennui éprouvés durant l’activité (« Je me suis ennuyé pendant le jeu »), la prise en main du jeu (par ex. « J’ai trouvé que le jeu était facile à utiliser »), ainsi que sur l’appréciation d’une telle activité (par ex. « J’aimerais pouvoir faire plus souvent des maths de cette manière-là ») et le sentiment d’avoir appris (par ex. « Je comprends mieux maintenant comment écrire un problème sous forme d’équation »).

De nombreuses données se rapportant à l’interaction entre le système et les utilisateurs ont, par ailleurs, été relevées lors des sessions de jeu et un certain nombre de séquences ont été enregistrées par capture d’écran vidéo. Dans le cadre de cette contribution, nous nous intéressons en particulier aux actions des joueurs qui dénotent une aisance ou au contraire des difficultés dans le jeu. L’aisance dans le jeu est mesurée par la rapidité à traverser les trois portes de la première partie du jeu et par le nombre de problèmes résolus dans la deuxième partie du jeu. A ce sujet, précisons que tous les élèves ont réussi à franchir les trois portes mais seule une minorité est parvenue à résoudre les trois problèmes à mettre en équation. L’éjection des portes, qui se produit lorsqu’un apprenant dépasse le temps imparti pour résoudre l’équation, a également été prise en considération. Les actions dénotant des difficultés ont été cernées notamment par l’utilisation répétée du bouton « recommencer » qui, selon la partie du jeu, va générer une nouvelle équation ou un nouveau problème de ficelle similaire alors que l’activité en cours n’est pas encore terminée, et par le recours régulier au bouton « annuler » qui autorise, lors de la simplification d’une équation, de revenir à l’état précédant la dernière action effectuée. L’examen de captures vidéo de sessions de jeu a montré que les apprenants qui recourent plus d’une fois au bouton « recommencer » rencontrent le plus souvent de sérieuses difficultés dans le jeu qu’ils ont de la peine à surmonter.

4. Résultats

4.1. Facteurs motivationnels issus de l’ACP

Une double analyse en composantes principales (ACP) sur les données des questionnaires passés avant le jeu (déterminants motivationnels) et après le jeu (qualité d’expérience du jeu) a permis de réduire le nombre d’items, en mettant en évidence des structures de corrélations.

Tableau 1. Analyse en composantes principales sur les aspects motivationnels (après rotation varimax avec normalisation Kaiser)

Trois facteurs sont mis en évidence dans l’ACP sur les aspects motivationnels (Tableau 1). Ils expliquent 64 % de la variance totale. Un premier axe concentre les items qui se réfèrent à une attitude marquée avant tout par le Plaisir à faire des maths. Un deuxième axe regroupe les items corrélés fortement autour de l’Intérêt pour le jeu à venir, donc pour l’activité proposée, mais se réfère aussi à la valeur attribuée aux jeux mathématiques en général. Le troisième axe, que nous avons intitulé Échec et math, se réfère au manque de sentiment de compétence des apprenants en mathématique, au sentiment d’anxiété et à la perception de la situation d’apprentissage comme un défi à relever (obstacle à surmonter) sans qu’y soit associé un sentiment de plaisir.

Cinq facteurs rendant compte de la qualité de l’expérience de jeu (Tableau 2) expliquent 67 % de la variance totale. Le premier facteur, que nous avons nommé le Sentiment d’avoir appris en s’amusant, associe le sentiment d’avoir acquis de nouvelles connaissances en algèbre élémentaire avec le plaisir d’avoir pu faire des mathématiques à travers un jeu vidéo. Les items conjuguant l’aspect « plaisir » et le « sentiment d’avoir appris » y sont fortement corrélés. Le deuxième facteur, Forte immersion dans le jeu, met l’accent sur le sentiment de s’être senti immergé dans le jeu au point de faire abstraction de son environnement immédiat. Les items qui lui sont associés reflètent en partie l’expérience du flow (distorsion du temps, oubli du lieu, sentiment d’être pris par le jeu, absence d’ennui). L’Effort mental soutenu se rapporte à des variables signalant que les ressources cognitives des apprenants étaient très fortement sollicitées durant le jeu. Le Sentiment d’aisance est un facteur relatif au sentiment de maîtrise de l’environnement d’apprentissage et de jeu par les élèves. Enfin, le cinquième facteur, Désorientation, désigne le sentiment de ne pas avoir toujours su quoi faire pour avancer dans le jeu.

Tableau 2 • Analyse en composantes principales sur l’expérience de jeu (après rotation varimax avec normalisation Kaiser)

A partir des différentes composantes mises en évidence par l’ACP, des corrélations ont été effectuées entre les facteurs « motivationnels », mesurés avant l’entrée dans l’activité et, d’une part, les variables de comportement et de progression dans le jeu et, d’autre part, les facteurs relatifs à la qualité d’expérience de jeu et au sentiment d’avoir appris de nouvelles notions en lien avec l’algèbre élémentaire.

Le premier facteur motivationnel, Plaisir à faire des mathématiques, est corrélé positivement avec le facteur Sentiment d’aisance dans le jeu, r = .24, p = .018, et négativement avec le facteur Désorientation, r = -.26, p = .010. Aucune corrélation significative ne peut être relevée entre le Plaisir à faire des mathématiques et les facteurs Sentiment d’avoir appris en s’amusant, Forte immersion dans le jeu ou Effort mental soutenu. Concernant les interactions du joueur avec le système de jeu, on constate que le facteur Plaisir à faire des mathématiques est corrélé négativement avec des variables de comportements révélant des temps d’hésitation ou de tâtonnement durant le jeu, qu’il s’agisse de l’activation du bouton « annuler » une dernière action, r = -.29, p = .020, ou du nombre de fois où le joueur est éjecté d’une porte en raison du dépassement du temps imparti pour résoudre l’équation, r = -.38, p < .001. Enfin, par rapport à la progression dans le jeu, le facteur Plaisir à faire des mathématiques est lié à un temps de jeu plus court lors du passage des trois portes, r = .42, p < .001, et à un plus grand nombre de problèmes résolus dans la deuxième partie du jeu, r = .33, p = .004.

Le deuxième facteur motivationnel, Échec et math, qui regroupe les variables dénotant un faible sentiment de compétence en mathématique, est associé au facteur Sentiment d’avoir appris en s’amusant, r = .27, p = .008, qui est lui-même corrélé avec le nombre de problèmes résolus dans la deuxième partie du jeu, r = .26, p = .023. Si on se penche de manière détaillée sur les différents items composant le facteur Sentiment d’avoir appris en s’amusant, on constate que le facteur Échec et math est corrélé avec les différents items constituant le volet « apprentissage » mais pas avec ceux composant le volet « amusement ». Aucune relation n’apparaît entre le facteur Échec et math et les facteurs Forte immersion dans le jeu, Effort mental soutenu et Désorientation, ni entre le facteur Échec et math et les différentes variables de comportement ou de progression dans le jeu.

Le troisième facteur motivationnel, Intérêt pour le jeu est corrélé, du point de vue de la qualité de l’expérience de jeu, avec le facteur Forte immersion dans le jeu, r = .24, p  = .020, caractérisé notamment par une forte immersion dans l’univers du jeu au point d’avoir le sentiment de s’être extrait du lieu de la classe et de ne plus avoir eu conscience du temps qui passait. Il est marginalement corrélé, r = .20, p = .055, au facteur Sentiment d’avoir appris en s’amusant, car il n’est associé qu’avec les items faisant référence à l’appréciation de l’activité et non pas à ceux attachés au sentiment d’avoir acquis de nouvelles connaissances. Par contre, aucune relation ne peut être établie entre l’Intérêt pour le jeu et les facteurs Effort mental soutenu et Désorientation. De même, aucune variable de comportement, qu’il s’agisse d’actions reflétant de l’indécision ou une progression rapide à travers les différents problèmes qui constituent le cœur du jeu, ne peut être mise en relation avec le plaisir de se lancer dans l’activité proposée.

4.2. Profils motivationnels d’élèves

Suite à l’ACP, nous avons procédé à une classification ascendante hiérarchique (CAH) en recourant à la méthode d’agrégation Ward pour mettre en évidence des profils d’élèves en fonction des scores factoriels issus de l’ACP sur les déterminants motivationnels. La méthode de Ward permet de regrouper au sein d’une même classe les individus qui se ressemblent plus et de maximiser l’inertie inter-classe afin d’obtenir des classes les plus homogènes possibles.

La CAH a produit quatre profils motivationnels d’élèves. Chacune des classes est structurée par la moyenne des scores factoriels significativement différents de la moyenne des élèves. Le premier groupe (n = 36), majoritaire, est constitué d’élèves qui n’ont pas de plaisir à faire des mathématiques, ont un sentiment moyen de compétence, mais sont curieux de connaître le jeu. Nous avons dénommé ce groupe « les Joueurs non matheux ». Le deuxième groupe (n = 25), intitulé « Les Mathématiciens curieux », se caractérise par des élèves qui aiment les mathématiques bien qu’ils se disent moyennement compétents, et qui sont curieux de connaître le jeu. Le troisième groupe (n = 12), qui compte le moins de sujets, regroupe les élèves qui se sentent très peu sûrs d’eux-mêmes en mathématique, mais qui ont malgré tout une attitude assez favorable envers cette discipline scolaire, et sont moyennement intéressés par le jeu : ce sont « les Peu Confiants ». Enfin, les élèves du quatrième groupe (n = 21) aiment moyennement les mathématiques et se sentent moyennement compétents dans cette branche ; ils ne sont pas du tout curieux de connaître le jeu. Nous les avons dénommés « les Inintéressés ».

Nous avons d’abord regardé si chacun des profils est cohérent avec la moyenne annuelle en mathématique et le score au pré-test algébrique, en procédant à des analyses de variance (Tableau 3). Les différences de moyennes entre les quatre groupes d’élèves sont significatives aussi bien pour la moyenne annuelle en mathématique, [F(3,89) = 4.66, p = .005, η² = .136], que pour le score au pré-test algébrique, [F(3,90) = 6.11, p = .001, η² = .169].

Tableau 3 • Moyenne annuelle en mathématique et score au pré-test selon les profils d’élèves (moyennes et écart-types)

Le groupe des Mathématiciens curieux a une moyenne annuelle en mathématique supérieure à celles des autres groupes, qui se distingue notamment (.77, p = .011) selon les tests post-hoc de Scheffé, de celle du groupe des Peu Confiants. Ces derniers sont les seuls à avoir une moyenne annuelle en mathématique qui est en deçà de celle exigée par le système scolaire suisse (moyenne fixée à 4). Les Mathématiciens curieux ont également un score au pré-test algébrique supérieur à celui des trois autres groupes. Cette différence est significative (17.07, p = 0.03) par rapport aux Joueurs non matheux et quasi significative (15.35, p = 0.87) par rapport aux Peu Confiants, sachant que la taille de ce groupe est comparativement plus petite (n = 12).

Les élèves se différencient-ils, selon leur profil motivationnel de départ, du point de vue de la qualité de l’expérience de jeu ? Les conditions d’homogénéité des variances n’étant pas respectées pour tous les scores factoriels, des tests non paramétriques ont été réalisés pour les facteurs concernés. Le test de Kruskal-Wallis nous indique que l’aisance dans le jeu (χ² = 9.14, p = .027) et le sentiment de désorientation et frustration (χ² = 8.32, p = .040) diffèrent significativement selon le profil des élèves. Les Mathématiciens curieux se sont sentis les plus à l’aise dans le jeu avec un rang moyen de 57, tandis que les Joueurs non matheux, dont le rang moyen est de 38, se sont sentis les moins à l’aise (Tableau 4). Les Peu Confiants, avec un rang moyen de 41, se sont également sentis, mais dans une moindre mesure, peu à l’aise dans le jeu. En cohérence avec le résultat précédent, ce sont les Mathématiciens curieux qui se sont sentis les moins désorientés en cours de jeu (rang moyen de 35 pour le facteur Désorientation) alors que les Peu Confiants sont les élèves qui ont le plus éprouvé le sentiment d’être perdus (rang moyen = 58).

Tableau 4 • Qualité de l’expérience de jeu selon les profils d’élèves (moyennes et écart-types)

Pour le facteur Sentiment d’avoir appris en s’amusant, les résultats globaux sont proches de la significativité [F(3,90) = 2.57, p = .059, η²  = .079], sans doute en raison de la différence de taille du groupe des Peu Confiants par rapport aux autres groupes. Le score moyen des Peu Confiants est nettement supérieur à celui des autres profils d’élèves (Tableau 4). Si l’on prend séparément les items du facteur Sentiment d’avoir appris en s’amusant, on relèvera, sur la base de tests de Kruskal-Wallis, des différences significatives entre les profils d’élèves pour l’appréciation de l’activité (p = .004), le sentiment que faire des maths de cette manière-là est intéressant (p = .001) et amusant (p = .002). Sur tous ces items, les Peu Confiants se distinguent significativement des Inintéressés : ils ont en moyenne des réponses positives pour chacun des ces items en comparaison avec les Inintéressés qui ont un avis plutôt négatif sur l’ensemble des questions relatives à l’appréciation de l’activité. Les différents profils d’élèves se distinguent aussi entre eux par rapport à l’impression de mieux comprendre certains concepts mathématiques à la suite du jeu [F(3,90) = 4.57, p = .043, η²  = .086], les Peu Confiants partageant le plus ce sentiment, tandis que les Inintéressés étaient plutôt en désaccord avec ce point de vue.

Aucun des profils d’élèves n’est associé à une forte immersion dans le jeu bien que deux groupes d’élèves (les Joueurs non matheux et les Mathématiciens curieux) se caractérisent au départ par une curiosité plus marquée pour le jeu que les deux autres groupes. Les élèves ayant pu vivre une expérience de forte immersion se retrouvent dispersés dans les différents groupes, mais sans aucun doute dans une proportion moindre chez les Inintéressés. Trois items sur six composant le facteur Forte immersion donnent des scores factoriels moyens différents selon les groupes d’élèves : il s’agit du sentiment que l’activité proposée relevait plus d’un exercice que d’un jeu [F(3,90) = 3.34, p = .023, η²  = .100], du sentiment de s’être ennuyé [F(3,90) = 4.38, p = .006, η² = .127], et de s’être senti pris par le jeu [F(3,90) = 3.99, p = .010, η² = .117]. Le sentiment de s’être ennuyé est le plus marqué chez les Joueurs non matheux (M = 2.64, ET = 1.07), suivi de près des Inintéressés (M = 2.52, ET = 1.25) et le moins prononcé chez les Mathématiciens curieux (M = 1.86, ET = .81) et les Peu Confiants (M = 1.75, ET = .75) ; à l’inverse, ces derniers sont ceux qui, parmi tous les groupes, se sont sentis le plus pris par le jeu, tandis que les Inintéressés l’étaient le moins.

Selon les analyses de comparaisons multiples de Scheffé, les différences sont significatives entre les Mathématiciens curieux et les Joueurs non matheux pour l’ennui éprouvé durant le jeu (-.78, p = .041), et entre les Peu Confiants et les Inintéressés pour le sentiment de s’être senti pris par le jeu (-.77, p = .038). On ne relève cependant pas de différences significatives entre les quatre groupes pour l’oubli du lieu et la distorsion du temps. En moyenne, les élèves ont tous eu le sentiment de n’avoir pas vu le temps passer ; par contre, ils n’ont pas eu, dans l’ensemble, le sentiment d’avoir oublié qu’ils étaient en classe. Quant au facteur Effort mental soutenu, il ne se distingue pas non plus d’un groupe d’élèves à l’autre.

Des différences dans le degré d’aisance dans le jeu ont également pu être observées selon le profil des joueurs. Le temps total moyen passé sur la première partie du jeu [F(3,86) = 2.65, p = .054, η² = .085], et le nombre de problèmes résolus dans la deuxième partie du jeu [F(3,84) = 3.08, p = .0.32, η²  = .099], varient selon les groupes d’élèves. Les Mathématiciens curieux réussissent toujours mieux que les autres, tandis que ce sont les Joueurs non matheux qui passent en moyenne le plus de temps sur les portes et qui résolvent le moins de problèmes dans la deuxième partie du jeu (Tableau 5). Ces derniers se distinguent significativement des Mathématiciens curieux (-.80, p = .044), selon les tests post-hoc de Scheffé pour le nombre de problèmes résolus. Les Peu Confiant, quant à eux, arrivent en deuxième position pour le nombre de problèmes résolus, devant les Joueurs non matheux et les Inintéressés.

Tableau 5 • Comportement dans le jeu selon les profils d’élèves (moyennes et écart-types)

D’autres variables dénotant des attitudes de tâtonnement ou d’hésitation, pour lesquels nous avons procédé à des tests non paramétriques en raison d’une absence d’homogénéité des variances, indiquent des différences de comportement selon les profils de joueurs. Selon le test de Kruskal-Wallis, la fréquence d’utilisation du bouton « annuler » la dernière action (p = .014) ainsi que le nombre d’éjections d’une porte dans la première partie du jeu (p = .016) en raison d’un dépassement du temps imparti pour résoudre une équation, varie selon le profil des élèves. Les Joueurs non matheux ont le plus tendance à activer le bouton « annuler », tandis que les Peu Confiants l’utilisent le moins souvent ; ce sont également les Joueurs non matheux qui subissent le plus d’éjections alors que les Mathématiciens curieux en sont le plus préservés.

5. Discussion

L’analyse en composantes principales combinée à la méthode de classification ascendante hiérarchique a permis de dégager différents profils d’élèves définis en fonction de leur attitude à l’égard des mathématiques, de leur sentiment de compétence dans cette discipline et de leur intérêt pour l’activité de jeu proposée.

L’analyse des différents profils motivationnels a mis en évidence deux types d’engagement dans le jeu sérieux liés à des orientations motivationnelles différentes au départ : d’un côté, nous avons identifié des apprenants orientés plutôt vers les contenus, de l’autre côté, des apprenants orientés plutôt vers le jeu ; une troisième catégorie d’apprenants, qui n’est intéressée ni par le contenu ni par le jeu, ne s’est pas réellement engagée dans les apprentissages visés par le jeu. Un engagement porté au départ par le contenu mathématique apparaît comme ayant été plus bénéfique, dans le cadre de notre jeu sérieux, en termes de motivation et d’expérience de jeu qu’un engagement motivé au départ essentiellement par l’intérêt pour le jeu.

Dans le premier groupe d’apprenants se trouvent les Mathématiciens curieux et les Peu confiants. Ils ont majoritairement apprécié Algebra Mystery, sans doute parce que le jeu sérieux a répondu à leurs attentes de départ, mais aussi parce que leur performance dans le jeu, tributaire de leur motivation intrinsèque pour les mathématiques, a contribué à ce sentiment de satisfaction. Ces deux profils d’élèves ont en commun un intérêt personnel pour le contenu mathématique, doublé d’un intérêt situationnel (Fredricks et al., 2004), (Murphy et Alexander, 2000) chez les Mathématiciens curieux, puisque ces derniers se disaient aussi curieux de découvrir le jeu. L’intérêt personnel conduit à un investissement plus important dans l’activité en raison d’un désir marqué d’acquérir de nouvelles compétences dans le champ en question (Eccles et Wigfield, 2002), (Hidi, 2001), (Linnenbrink et Pintrich, 2003).

Les apprenants-joueurs qui avaient avant tout un intérêt pour les contenus d’apprentissage au départ du jeu, ont fait preuve d’un engagement élevé dans le jeu, ils ont été persévérants tout au long de l’activité malgré les obstacles rencontrés. Leur comportement dans le jeu s’est caractérisé par la volonté de comprendre les mécanismes du jeu ainsi que le contenu pédagogique qui lui était étroitement associé, ce qui s’est traduit par des réussites tout au long du jeu. La conception d’un jeu fortement axé sur les mathématiques, correspondant sans doute en partie aux attentes des apprenants, ainsi que le fait de pouvoir se rendre compte des progrès réalisés (résoudre les équations et les problèmes mathématiques) et de se sentir compétents dans l’activité menée ont dû avoir un effet positif sur leur engagement et renforcer celui-ci (Whitton, 2010).

Une partie des apprenants orientés « contenu », les Peu Confiants, ont déclaré avant le jeu avoir un faible sentiment d’efficacité personnelle dans la résolution de problèmes. Il s’agit d’apprenants qui ont sans doute en général de la peine à s’engager dans une activité mathématique et à se sentir compétents pour la mener à terme. Ils ont d’ailleurs fait part au début d’un faible intérêt pour le jeu, même s’ils ont une attitude favorable à l’égard des mathématiques, faible intérêt qui s’explique peut-être par des expériences passées négatives en mathématique ou est le fruit d’un certain scepticisme quant à l’efficacité des jeux pour apprendre les mathématiques. L’attitude circonspecte par rapport au jeu proposé n’a toutefois pas eu d’incidence négative sur leur engagement et leur motivation à réussir.

Un simple habillage des tâches mathématiques n’est pourtant souvent pas suffisant pour induire un véritable engagement dans les apprentissages pour des élèves en difficulté scolaire et les inciter à l’action (Pelgrims et Cèbe, 2010). On peut supposer que la conception d’un jeu centré sur le contenu pédagogique, ne contenant pas d’éléments distractifs, ainsi que la présence de feedbacks, informant immédiatement les apprenants de la validité de leurs actions, ont permis aux élèves peu confiants de réguler leurs actions au fur et à mesure de leur avancement dans le jeu, ce qui a dû favoriser leur engagement et leur persévérance dans le jeu et contribuer à leur progression (Cameron et Dwyer, 2005), (Gunter et al., 2008). Un environnement d’apprentissage en ligne a aussi comme avantage de ne pas émettre de jugement de valeur sur les erreurs commises et peut de ce fait avoir un effet rassurant pour ce profil de joueurs. Aucun de ces élèves n’a abandonné en cours de route le jeu, même si certains d’entre eux ont rencontré des difficultés dans la prise en main du logiciel, alors que ce sont des élèves qui ont sans doute souvent été confrontés à des échecs et ont pu développer au cours du temps des comportements d’évitement (Pelgrims et Cèbe, 2010). En laissant peu de place à des stratégies d’essais-erreurs et en fournissant des rétroactions immédiates, Algebra Mystery a certainement encouragé ces élèves à attribuer leurs réussites et échecs à leurs propres actions, plutôt qu’à des causes externes incontrôlables qui ont un effet négatif sur la motivation (Graham et Williams, 2009), et leur a donné le sentiment d’avoir acquis de nouvelles connaissances en mathématique.

Par contre, les apprenants-joueurs qualifiés de Joueurs non matheux, qui étaient au départ essentiellement motivés à s’engager dans Algebra Mystery en raison de leur intérêt pour le jeu, mais qui n’avaient pas de plaisir à faire des mathématiques, ne sont pas parvenus à surmonter certaines des difficultés auxquelles ils ont été confrontés durant le jeu, ce qui a empêché une véritable entrée dans les apprentissages. Leur engagement initial, orienté sur le « jeu » n’a pas coïncidé avec un engagement cognitif dans les contenus didactiques ; il s’est délité au fur et à mesure des problèmes rencontrés, qui relevaient soit du contenu didactique soit de la prise en main des mécaniques de jeu ou des deux à la fois, s’agissant d’un jeu intrinsèquement intégré.

Plusieurs des facteurs considérés comme ayant un effet négatif sur l’engagement (Whitton, 2010) ont joué en défaveur de ces apprenants, tels que des difficultés à démarrer dans la deuxième partie du jeu, le fait d’être restés bloqués dans le premier problème pour une majorité d’entre eux, et un ennui intrinsèque manifesté pour le contenu ou l’activité elle-même. Face à un jeu centré essentiellement sur un contenu d’apprentissage, les Joueurs non matheux ont sans doute eu le sentiment que le jeu proposé, tel qu’il était conçu, ne contenait pas suffisamment de ressorts ludiques. Lorsque la motivation porte essentiellement sur le jeu et que la motivation intrinsèque pour le contenu pédagogique fait totalement défaut, voire que des émotions négatives sont ressenties par rapport à celui-ci, il semble difficile de reporter l’intérêt pour le jeu sur le contenu d’apprentissage lorsque celui-ci est prédominant dans l’environnement d’apprentissage. Il serait sans doute souhaitable, pour maintenir l’engagement de cette catégorie d’apprenants-joueurs, de concevoir un environnement qui contienne plus d’éléments ludiques, dans l’idée qu’en soutenant un engagement orienté sur le jeu, on assiste à un effet contagieux sur l’engagement dans les contenus d’apprentissage.

Enfin, les joueurs-apprenants qui n’étaient particulièrement intéressés ni par le contenu ni par le jeu, se sont sentis moins motivés à s’engager dans un jeu pédagogique même si ce sont des apprenants qui n’avaient pas de difficultés majeures dans le champ disciplinaire dans lequel s’inscrit le jeu. Il semble difficile de faire entrer dans un jeu des élèves très peu intéressés au départ par l’activité qui leur est proposée, voire qui lui sont hostiles. Ce résultat confirme le rôle central que joue l’intérêt pour un contenu ou une tâche dans l’envie de s’engager dans une activité (Linnenbrink et Pintrich, 2003). Une attitude détachée dès le départ et qui se maintient tout au long du jeu se traduit par une absence d’apprentissage, même si certains de ces apprenants ont passé le cap du premier problème. Un accompagnement particulier ou une introduction au jeu seraient peut-être efficaces pour assurer un engagement cognitif et comportemental, voire émotionnel, plus important de ces élèves afin de leur assurer une plus grande satisfaction et une progression plus importante dans les apprentissages visés par un jeu.

Les profils dégagés ont donc révélé des attentes et des motivations variées chez les joueurs qui se sont traduites par différents types de comportements d’engagement dans le jeu et par une qualité d’expérience différenciée selon les profils. D’autres études ont également montré pour les jeux vidéo que l’attention et la conscience des joueurs pouvaient être tournées vers des éléments distincts, notamment soit vers l’environnement du jeu soit vers le jeu lui-même (Bouvier et al., 2014). L’engagement apparaît donc comme un état qui se manifeste et se maintient dans un jeu sérieux lorsque la forme du jeu et ses contenus pédagogiques coïncident avec les attentes et les intérêts des apprenants-joueurs. Dans le cas d’un jeu sérieux comme Algebra Mystery qui privilégie des contenus complexes, entièrement ou partiellement nouveaux pour ses utilisateurs, et où les formes du jeu pourraient être davantage développées, ce ne sont finalement pas les « joueurs » mais les « sérieux » qui ont le plus progressé dans le jeu et se sont déclarés les plus satisfaits de l’activité.

L’ACP a montré, par ailleurs, un lien clair entre la curiosité a priori avant le jeu et une forte immersion dans l’univers fictif du jeu, sans qu’on puisse néanmoins relever un lien entre une expérience de jeu que l’on peut qualifier de proche d’un état de flow (plaisir, absence d’ennui et déconnexion temporelle et spatiale) et la progression dans la résolution des problèmes. Il semble donc que l’état d’expérience optimale n’est pas forcément propice à un engagement cognitif dans la tâche d’apprentissage et dans la prise de conscience des concepts mathématiques sous-jacents dans le jeu (Klawe, 1998).

Aucun des profils d’élèves n’est associé à une forte immersion dans le jeu bien que deux groupes d’élèves (Les Joueurs non matheux et les Mathématiciens curieux) se caractérisent au départ par une curiosité plus marquée pour le jeu que les deux autres groupes. Les Peu confiants se distinguent cependant des Inintéressés en affirmant s’être sentis pris par le jeu et ne pas s’être ennuyés mais d’autres dimensions importantes du flow comme l’oubli du lieu ou la distorsion du temps ne sont pas l’apanage d’un groupe par rapport à un autre. Les élèves ayant pu vivre une expérience de forte immersion se retrouvent dispersés dans les différents groupes, mais sans aucun doute dans une proportion moindre chez les Inintéressés. La nouveauté du jeu, les difficultés de prise en main et le contexte d’utilisation de la classe ont sans doute rendu difficile l’émergence et le maintien tout au long du jeu d’une expérience proche du flow.

6. Conclusion

Nous avons évalué dans cette étude les aspects motivationnels d’un jeu vidéo destiné à l’apprentissage de concepts algébriques. Les résultats indiquent, en lien avec nos questions de recherche, que les prédispositions motivationnelles des apprenants, mesurées avant l’engagement dans le jeu, peuvent être mises en relation avec certains comportements durant le jeu, avec la difficulté ou la facilité de la prise en main de l’environnement d’apprentissage/jeu, ainsi qu’avec la qualité de l’expérience, mais aussi avec la perception qu’ont les apprenants/joueurs d’avoir acquis ou non de nouvelles connaissances suite à l’activité proposée. En particulier, différents profils d’élèves ont pu être dégagés à partir des déterminants motivationnels, ce qui a permis de montrer que les notions de plaisir à jouer, de progression dans le jeu, de capacité à surmonter les obstacles, d’immersion et de perception de l’apprentissage ne sont pas liés de manière simple et directe mais sont le produit d’une configuration complexe.

Sur le plan de la motivation, l’expérience menée avec Algebra Mystery a confirmé que l’intérêt pour une activité, conformément à la théorie de l’intérêt, joue un rôle déterminant dans l’engagement des élèves dans une activité donnée. Néanmoins, dans le cas d’un jeu sérieux, l’orientation de l’intérêt, selon qu’il porte sur le jeu, le contenu d’apprentissage, ou les deux à la fois, semble avoir une influence prépondérante sur le degré d’engagement cognitif et la qualité de l’expérience de jeu des joueurs-apprenants. Par ailleurs, à moins d’un intérêt complètement absent, voire d’une attitude négative envers l’activité proposée, qui rend très difficile tout engagement et persistance, la nature de l’environnement d’apprentissage et la qualité de l’interaction entre l’apprenant et cet environnement est susceptible de faire naître en cours de jeu un intérêt grandissant pour l’activité, même si au départ celui-ci était faible, et conduire à l’engagement cognitif et émotionnel des intéressés. Des élèves a priori peu confiants, qui ont un sentiment d’efficacité personnelle moindre, semblent bénéficier d’un environnement d’apprentissage interactif et ludique qui fournit des feedbacks immédiats sur chacune des actions menées.

Mieux connaître à l’avance les prédispositions motivationnelles des joueurs-apprenants pourrait donc servir à orienter ces derniers de manière plus efficace vers telle ou telle activité pédagogique et de prévoir des mesures d’accompagnement adaptées en fonction du profil de chaque joueur-apprenant. Dans le cas des « joueurs » peu intéressés au départ par le contenu didactique, l’entrée dans les apprentissages pourrait se faire plus progressivement, des intermèdes de « pur jeu » pourraient être proposés à certains moments du jeu tout en conservant en parallèle des contenus d’apprentissage intégrés dans la mécanique du jeu. On peut dès lors se demander si un accent mis sur l’apprentissage durant tout le temps du jeu, à travers chacune des actions du jeu, est toujours profitable en matière d’engagement pour les profils de « purs joueurs » qui estiment qu’il y a insuffisamment de jeu et d’actions et trop de contenu pédagogique.

Il serait, par ailleurs, important de mener une analyse didactique des interactions entre le joueur et l’environnement de jeu afin de mettre en évidence les difficultés rencontrées par les joueurs dans leur compréhension des notions mathématiques sous-jacentes et d’établir précisément dans quelle mesure l’environnement proposé, qui comportait différentes représentations des objets mathématiques, a contribué, pour chacun des profils motivationnels, à la construction des connaissances mathématiques visées par le jeu.  

7. Remerciements

Nous tenons à remercier les enseignants du Cycle d’Orientation des Colombières qui ont participé à la phase d’expérimentation du projet et notamment Gabriel Thullen qui a suivi le projet dès sa phase de conception. Nous remercions également Nicolas Habonneau pour le développement d’Algebra Mystery ainsi que la Commission informatique de l’Université de Genève qui a soutenu financièrement le projet.

À propos des auteurs

Denise Sutter Widmer est chargée d’enseignement à l’Université de Genève. Elle forme les étudiants engagés dans la formation en enseignement primaire à l’usage pédagogique des MITIC.  Au bénéfice d’une licence en histoire économique et sociale et d’un master en administration publique, Denise Sutter Widmer a travaillé quelques années dans différents secteurs (administration publique, milieu associatif et enseignement) avant de s’intéresser aux technologies éducatives. Ses thèmes de recherche concernent les jeux destinés à l’apprentissage. Sa thèse, soutenue en janvier 2017, portait sur la conception et l’évaluation d’un jeu sérieux en algèbre. Elle s’intéresse également à l’intégration des technologies éducatives dans les classes.

Adresse : TECFA-FPSE Université de Genève – Uni-Pignon, Pont d'Arve 40, 1211 Genève 4, Suisse

Courriel : denise.sutterwidmer@unige.ch

Toile : tecfa.unige.ch/perso/sutterw/

Nicolas Szilas est ingénieur de l’ESIM (Ecole Centrale Marseille) et docteur de l’INPG en Sciences Cognitives. Du public au privé et vice-versa, il a acquis une compétence pluridisciplinaire dans les domaines de l’Intelligence Artificielle, de l’Interface Homme Machine et des jeux vidéo. En 1999, il lance IDtension, un programme de recherche sur le Drame Interactif, qui devra devenir son domaine d'excellence pour les années à venir. En 2006, il entre au laboratoire TECFA de l'Université de Genève, où il poursuit ces recherches au travers de plusieurs projets financés par l'Europe ou la Suisse. Il s'intéresse particulièrement à l'utilisation de ces systèmes à des fins d'apprentissage ou de formation, au développement de modèles, outils et méthodologies permettant à des auteurs de s'approprier ces nouvelles technologies d'écriture, et enfin à leur évaluation. Il s'intéresse également de près aux jeux vidéo pédagogiques, domaine qu'il enseigne à l'Université, notamment aux questions d'intégration des objectifs pédagogiques dans la mécanique de jeu.

Adresse : TECFA-FPSE Université de Genève – Uni-Pignon, Pont d'Arve 40, 1211 Genève 4, Suisse

Courriel : nicolas.szilas@unige.ch

Toile : tecfa.unige.ch/perso/szilas/

BIBLIOGRAPHIE

Ainsworth, S. (1999). Designing effective multi-representational learning environments. ESRC Centre for Research in Development, Instruction & Training, Department of Psychology, University of Nottingham, 58. Disponible sur internet. 

Barr, P., Noble, J. et Biddle, R. (2007). Video game values: Human–computer interaction and games. Interacting with Computers, 19(2), 180–195.

Bourgeois, E. (2011). La motivation à apprendre. Dans E. Bourgeois et G. Chapelle (dir.), Apprendre et faire apprendre (2nd ed., p. 235–253). Paris : Presses Universitaires de France.

Bouvier, P., Lavoue, E. et Sehaba, K. (2014). Defining engagement and characterizing engaged-behaviors in digital gaming. Simulation & Gaming, 45(4–5), 491–507.

Bransford, J. D., Brown, A. L. et Cocking, R. R. (2000). How people learn: Brain, mind, experience and school. Washington, DC : National Academy Press.

Brockmyer, J. H., Fox, C. M., Curtiss, K. A., Mcbroom, E., Burkhart, K. M. et Pidruzny, J. N. (2009). The development of the Game Engagement Questionnaire: A measure of engagement in video game-playing. Journal of Experimental Social Psychology, 45(4), 624–634.

Brown, E. et Cairns, P. (2004). A grounded investigation of game immersion. Dans Proceedings of the Conference on Human Factors in Computing Systems (CHI 2004) (p. 1297-1300). ACM Press.

Cameron, B. et Dwyer, F. (2005). The effect of online gaming, cognition and feedback type in facilitating delayed achievement of different learning objectives. Journal of Interactive Learning Research, 16(3), 243–258.

Csikszentmihalyi, M. (1990). Flow: the psychology of optimal experience. New York, NY : Harper.

Csikszentmihalyi, M. et Nakamura, J. (1989). The dynamics of intrinsic motivation: A study of adolescents. Dans C. Ames & R. Ames (dir.), Research on motivation in education (Vol. 3, p. 45–71). San Diego, CA : Academic Press.

Duval, R. (1993). Registres de représentation sémiotique et fonctionnement cognitif de la pensée. Annales de Didactique et de Sciences Cognitives, 5, 37–65.

Duval, R. (2002). Comment décrire et analyser l’activité mathématique ? Cadres et registres. Dans Actes de la journée en hommage à Régine Douady (p. 83–105). Paris, France : IREM, Université Paris 7 Denis Diderot. Disponible sr internet.

Eccles, J. S. et Wigfield, A. (2002). Motivational beliefs, values, and goals. Annual Review of Psychology, 53, 109–132.

Egenfeldt-Nielsen, S. (2005). Beyond edutainment. Exploring the educational potentials of computer (Thèse, IT-University of Copenhagen, Danemark).

Esteban-Millat, I., Martínez-López, F. J., Huertas-García, R., Meseguer, A. et Rodríguez-Ardura, I. (2013). Modelling students’ flow experiences in an online learning environment. Computers & Education, 71, 111-123.

Fredricks, J. A., Blumenfeld, P. C. et Paris, A. H. (2004). School engagement: Potential of the concept, State of the Evidence. Review of Educational Research, 74(1), 59–109.

Garris, R., Ahlers, R. et Driskell, J. E. (2002). Games, motivation, and learning: A research and practice model. Simulation & Gaming, 33(4), 441–467.

Graham, S. et Williams, C. (2009). An attributional approach to motivation in school. Dans K. Wentzel et A. Wigfield (dir.), Handbook of motivation at school (p. 11–33). London, United Kingdom : Routledge.

Gunter, G. A., Kenny, R. F. et Vick, E. H. (2008). Taking educational games seriously: Using the RETAIN model to design endogenous fantasy into standalone educational games. Educational Technology Research and Development, 56(5–6), 511–537.

Habgood, J. (2007). The effective integration of digital games and learning content (Thesis, University of Nottingham, U.K.). Disponible sur internet.

Habgood, J. et Ainsworth, S. (2011). Motivating children to learn effectively: Exploring the value of intrinsic integration in educational games. The Journal of the Learning Sciences, 20(2), 169–206.

Hidi, S. (2001). Interest, reading, and learning: Theoretical and practical considerations. Educational Psychology Review, 13(3), 191–209.

Jennett, C., Cox, A. L., Cairns, P., Dhoparee, S., Epps, A., Tijs, T. et Walton, A. (2008). Measuring and defining the experience of immersion in games. International Journal of Human-Computer Studies, 66(9), 641–661.

Klawe, M. (1998). When does the use of computer games and other interactive multimedia software help students learn mathematics? Disponible sur internet (consulté le 25 novembre 2016).

Lazzaro, N. (2004). Why we play game: Four keys to more emotion without story.  Repéré sur le site de Xeodesign à http://xeodesign.com/xeodesign_whyweplaygames.pdf (consulté le 25 novembre 2016).

Linnenbrink, E. A. et Pintrich, P. R. (2003). The role of self-efficacy beliefs in student engagement and learning in the classroom. Reading & Writing Quarterly, 19(2), 119–137.

Malone, T. W. (1981). Toward a theory of intrinsically motivating instruction. Cognitive Science, 5(4), 333–369.

Malone, T. W. et Lepper, M. R. (1987). Making learning fun : a taxonomy of intrinsic motivations for learning. Dans R. E. Snow et M. J. Farr (dir.), Aptitude, learning and instruction : III. Conative cognitive and affective process (p. 222–253). Hilsdale, NJ : Erlbaum.

Mayer, R. E. (2007). Learning and instruction (2nd ed.). Pearson.

Michael, D. et Chen, S. (2006). Serious Games: Games That Educate, Train, and Inform. Boston, MA: Thomson.

Mitchell, A. et Savill-Smith, C. (2004). The use of computer and video games for learning. A review of the literature. London, United Kingdom : Learning and Skills Development Agency.

Murphy, P. K. et Alexander, P. A. (2000). A motivated exploration of motivation terminology. Contemporary Educational Psychology, 25, 3–53.

O’brien, H. L. et Toms, E. G. (2008). What is user engagement? A conceptual framework for defining user engagement with technology. Journal of the American Society for Information Science and Technology, 59(6), 938–955.

Pelgrims, G. (2009). Contraintes et libertés d'action en classe spécialisée : leurs traces dans la motivation des élèves à apprendre les mathématiques. Formation et pratiques d’enseignement en questions, 9, 135–158. Disponible sur internet.

Pelgrims, G. et Cebe, S. (2010). Aspects motivationnels et cognitifs des difficultés d’apprentissage : le rôle des pratiques d’enseignement. Dans M. Crahay et M. Dutrévis (dir.), Psychologie des apprentissages scolaires (p. 111–135). Bruxelles, Belgique : De Boeck.

Rathunde, K. et Csikszentmihalyi, M. (2005). Middle school students’ motivation and quality of experience : A comparison of Montessori and traditional school environments. American Journal of Education, 111(3), 341–371.

Ryan, R. M. et Deci, E. L. (2009). Promoting self-determined school engagement. Dans K. Wentzel et A. Wigfield (dir.), Handbook of motivation at school (p. 171–195).  London, United Kingdom : Routledge.

Salen, K., Nowacek, N., Tandon, R., Nunez, E. et Jenson, T. (2009). Gamestar mechanic, Learning guide. Institute of Play.

Salen, K. et Zimmerman, E. (2004). Rules of play: game design fundamentals. Cambridge, MA : The MIT Press.

Salomon, G. (1972). Can we affect cognitive skills through visual media? An hypothesis and initial findings. AV Communication Review, 20(4), 401–422.

Schunk, D. H., Meece, J. et Pintrich, P. R. (2014). Motivation in education: Theory, research, and applications (4th ed.). Pearson Education.

Sutter Widmer (2017), Conception et évaluation d'un jeu vidéo en algèbre : Apprentissage, motivation et usage de la visualisation dans un environnement aux représentations multiples (Thèse de doctorat). Université de Genève, Suisse.  

Szilas, N. et Sutter Widmer, D. (2009). Mieux comprendre la notion d’intégration entre l’apprentissage et le jeu. Dans Actes de l'Atelier Jeux Sérieux - Conférence francophone Environnements Informatiques pour l’Apprentissage Humain (EIAH'09) (p. 27-40). Disponible sur internet.

Tapia, M., Marsh, I. et George, E. (2004). An instrument to measure mathematics attitudes. Academic Exchange Quarterly, 8(2), 2–9.

Viau, R. (1998). La motivation en contexte scolaire (2nd ed.). Bruxelles, Belgique : De Boeck.

Vogel, M., Girwidz, R. et Engel, J. (2007). Supplantation of mental operations on graphs. Computers & Education, 49(4), 1287–1298.

Whitton, N. (2010). Game engagement theory and adult learning. Simulation & Gaming, 42(5), 596–609.

Référence de l'article :

Denise SUTTER WIDMER, Nicolas SZILAS, Motivation, comportement dans le jeu et expérience de jeu : une relation aux multiples facettes, Revue STICEF, Volume 24, numéro 1, 2017, DOI:10.23709/sticef.24.1.10, ISSN : 1764-7223, mis en ligne le 02/06/2017, http://sticef.org