Sommaire

Rechercher

• auteur
• année
• titre
• résumé
• abstract
• rubrique

Contact : infos@sticef.org

Une ressource virtuelle de résolution de problèmes mathématiques : les perceptions d’utilisateurs et les traces d’usage

Viktor FREIMAN (Université de Moncton, Canada), Dominic MANUEL, (Université McGill, Canada)

RÉSUMÉ : De quelle façon l’usage des ressources virtuelles change la perception d’enseignement et d’apprentissage de mathématiques chez les enseignants et leurs élèves ? Une étude de valeur ajoutée d’expériences de résolution de problèmes mathématiques dans un espace numérique collectif nous dresse une perspective complexe et authentique : en construisant leurs démarches à l’aide des outils virtuels, les élèves semblent apprécier des nouveaux outils de communication et de raisonnement mathématique qui leur apportent des occasions de relever le défi, le sens d’autonomie, et de satisfaction personnelle tout en contribuant à de multiples échanges et collaborations. Comment on met cet enthousiasme naturel au profit de l’amélioration des apprentissages mathématiques dans un contexte de résolution de problèmes demeure toutefois une question ouverte. MOTS CLÉS : Communication et raisonnement mathématiques, résolution de problèmes, ressources virtuelles d’apprentissage, perceptions des élèves et des enseignants.

ABSTRACT : How does the use of virtual learning environment change the perception of teaching and learning in students and teachers? An analysis of add-on value of mathematical problem solving activities in a collective digital space provides us with a better insight on the complexity and authenticity of the experience: while elaborating the solutions, students seem to appreciate new tools of mathematical communication and reasoning, as they report having a sense of a good challenge, autonomy and personal satisfaction; these tools also seem to contribute to the multiple opportunities of exchanges and collaboration. However, more research evidence is needed to convert this moment of overall excitement into the improvement of the learning of mathematics in a context of problem-solving. KEYWORDS : Mathematical communication and reasoning, problem solving, virtual learning communities, students’ and teachers’ perceptions

• 1. Introduction — Les technologies de l’information et de la communication (TIC) pour soutenir la résolution de problèmes en mathématiques : quel appui pour la réforme?
• 2. Résolution de problèmes : un défi pour l’élève et l’enseignant
• 3. Historique et aperçu global de la communauté virtuelle CAMI : quel apport à l’apprentissage ?
• 4. Perceptions des élèves et des enseignants par rapport à la ressource et aux nouvelles occasions d’apprentissage
• 5. Communication de la démarche de résolution de problèmes dans un environnement virtuel : parler mathématique à l’aide des TIC
• 6. Conclusion
• BIBLIOGRAPHIE

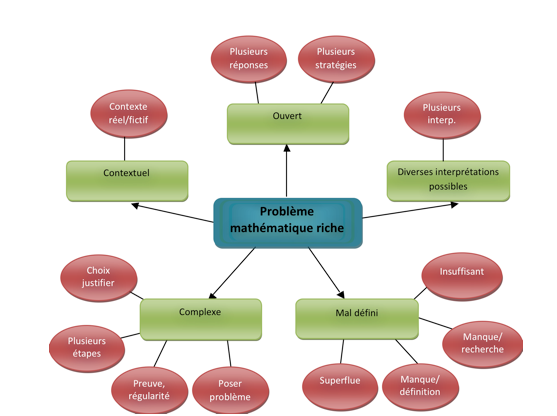
1. Introduction — Les technologies de l’information et de la communication (TIC) pour soutenir la résolution de problèmes en mathématiques : quel appui pour la réforme?

Au début du 21e siècle, la résolution de problèmes est devenue un élément central de l’enseignement de mathématiques en Amérique du Nord. L’habileté de pouvoir résoudre des problèmes fait ainsi partie des Principes et des standards (Principles and Standards) du Conseil national des enseignants des mathématiques des États-Unis (NCTM, 2001), une compétence clé dans le Programme de formation de l’école québécoise (MEQ, 2001), et dans les nouveaux programmes d’études des mathématiques au Nouveau-Brunswick (MÉDPENB, 2011). Entre autres, ces réformes mettent en évidence le besoin de développer chez l’élève des habiletés à communiquer mathématiquement, à raisonner mathématiquement et à établir des liens par l’entremise de situations-problèmes complexes et contextualisées dont la démarche de résolution n’est pas connue préalablement par l’élève. Ce dernier doit donc la construire. Or, les examens provinciaux instaurés par le MÉDPENB qui mesurent ces habiletés chez les élèves francophones du Nouveau-Brunswick (30 % de la totalité de l’examen) démontrent peu d’amélioration des résultats, ce qui semble être confirmé par l’évolution du rendement dans les études internationales mises en place par l’Organisation de la coopération et du développement économique (OCDE) depuis 2000 où ces mêmes habiletés sont associées à la culture mathématique chez les jeunes de 15 ans (OCDE, 2000).

Tout comme Corbeil, et al. (Corbeil et al., 2001) et Pallascio (Pallascio, 2005), nous attribuons les défis du développement des habiletés en résolution de problèmes mathématiques complexes au changement de paradigmes en priorisant la production de solutions plus authentiques par chaque élève, lui permettant de (d’) :

- explorer l’énoncé en profondeur en y repérant les informations utiles et les objectifs (buts) à atteindre ;

- formuler des hypothèses et des conjectures ;

- intérioriser des « règles de jeu » ;

- développer des habiletés à chercher, créer, utiliser son intuition, analyser, synthétiser, justifier et anticiper le résultat ;

- mobiliser et utiliser de façon efficace les ressources pour décrire une ou plusieurs réponses qui ne sont pas préalablement connues.

Les recherches semblent indiquer que ce changement n’a pas encore eu l’impact voulu sur les pratiques d’enseignement et d’apprentissage dans les salles de classe. Entre autres, Chan (Chan, 2008) rapporte qu’au lieu d’être placés au centre de leurs apprentissages, les élèves se trouvent encore confrontés à des exercices répétitifs de reproduction d’algorithmes présentés par leur enseignant de façon magistrale. Dans ces types d’activités mathématiques, les priorités sont surtout accordées à l’exactitude des calculs (l’obtention de la bonne réponse) ainsi qu’à la rapidité d’exécution, souvent au détriment de la créativité (Mann, 2005).

Les élèves, de leur côté, se construisent un système de règles souvent implicites à partir de leurs expériences en résolution de problèmes. Un tel contrat didactique, selon Poirier (Poirier, 2001), peut entrainer, entre autres, la recherche par l’élève d’une seule bonne réponse en utilisant toutes les données du problème et en appliquant les procédures de calcul récemment apprises en classe. Manuel (Manuel, 2010) s’interroge sur l’impact de ce type de règles sur la créativité des élèves quant à l’élaboration de leurs propres stratégies et à la recherche de solutions originales. Il se demande également si l’émergence des environnements virtuels d’apprentissage, de nature plus collaborative et authentique, aurait du potentiel à favoriser les apprentissages plus authentiques chez les élèves aux prises avec les problèmes complexes leur présentant un défi de taille.

Notre article a pour but d’analyser les perceptions des élèves et des enseignants quant à l’usage du site Internet CAMI (Communauté d’apprentissages multidisciplinaires interactifs, www.umoncron.ca/cami) créé en 2000 sous forme d’un Chantier d’Apprentissages Mathématiques Interactifs (Freiman et al., 2005b) qui a évolué, au fil des années, en une communauté virtuelle CASMI (Communauté d’apprentissages scientifiques et mathématiques interactifs), (Freiman et Lirette-Pitre, 2009b) en devenant par la suite multidisciplinaire. Cette ressource en ligne, qui propose des problèmes mathématiques authentiques et complexes, a été développée à l’Université de Moncton et est avant tout destinée aux élèves francophones du Nouveau-Brunswick et d’ailleurs au Canada, mais grâce à sa nature ouverte et à l’accès libre, elle peut être utilisée partout dans le monde (Freiman et al., 2007) ; (Freiman et Lirette-Pitre, 2009a).

En nous questionnant sur la valeur ajoutée à la communauté CAMI pour (1) enrichir l’enseignement et l’apprentissage des mathématiques en général et (2) pour inciter les élèves à produire des démarches de résolution de problèmes plus détaillées et cohérentes en se servant des outils de communication dans un espace virtuel, nous analysons dans cet article deux types de données : des entrevues semi-dirigées faisant ressortir des perceptions des élèves et de leurs enseignants par rapport à l’expérience de résolution de problèmes en ligne et les traces d’usage numériques qui documentent la communication de démarches de résolution de problèmes construites par les élèves à l’aide des outils virtuels.

2. Résolution de problèmes : un défi pour l’élève et l’enseignant

En construisant les fondements de sa théorie des situations didactiques, Brousseau (Brousseau, 1998) fait part des difficultés des chercheurs à définir la notion de problèmes dans le contexte de l’enseignement des mathématiques. Selon lui, « ces difficultés commencent lorsqu'il s'agit de savoir quels problèmes il doit se poser, qui les pose, et comment » (Brousseau, 1998), p. 115. Plusieurs auteurs s’intéressent à donner un sens didactique (ou trouver une « niche didactique », d’après Houdement (Houdement, 2009) à l’utilisation de problèmes « pour chercher » ou « complexes ». Il s’agit, selon l’auteure, de faire ressortir « des bénéfices pour les élèves de séances bien pensées de ces problèmes, il se pourrait que réfléchir aux types de connaissances effectives déclenchées par de telles séances et lister les conditions de ces déclenchements mettent à jour des connaissances ignorées (des professeurs et même des chercheurs), non simplement institutionnalisables, que possèderaient certains élèves et qui seraient très utiles (voire nécessaires) pour les apprentissages mathématiques ordinaires » (Houdement, 2009), p. 6.

À ces enjeux liés à la nature des problèmes et à leurs multiples rôles dans le processus d’enseignement et d’apprentissage des mathématiques s’ajoutent les difficultés à construire un processus de résolution de problèmes par l’élève. Julo (Julo, 1995) avance que ce processus est non linéaire faisant intervenir, déjà au stade de la représentation, plusieurs processus simultanément dont celui d’interprétation et de sélection, celui de structuration et d’opérationnalisation.

Dans leur étude portant sur la créativité en résolution de problèmes, Manuel et al. (Manuel et al., 2012) ont exploré en profondeur la notion de richesse d’un problème. Pour définir le problème mathématique riche, les auteurs ont retenu des critères pouvant être évalués dans les énoncés des problèmes. Selon différents auteurs, un problème est riche lorsqu’il est ouvert (Arsac et Mante, 2005) ; (Diezmann et Watters, 2004) ; (Takahashi, 2000), complexe (Diezmann et Watters, 2004) ; (Schleicher, 1999), mal défini (Murphy, 2004), contextualisé (Greenes, 1997) et possède diverses interprétations possibles (Hancock, 1995). Plus précisément, le problème est ouvert s’il contient plusieurs réponses correctes possibles ou peut se résoudre en utilisant plusieurs stratégies (Takahashi, 2000). Le problème complexe respecte le plus de critères parmi les suivants : il se résout en utilisant plus d’une étape ; il demande implicitement ou explicitement de trouver des régularités, de généraliser des résultats ou de faire des preuves mathématiques ; il demande explicitement de faire des choix et de les justifier, et il demande explicitement de poser d’autres problèmes afin de continuer l’exploration. Un problème est mal défini s’il lui manque certaines données importantes ou nécessaires, mais qui peuvent être définies ou recherchées, s’il inclut des données superflues ou encore, s’il ne fournit pas les informations suffisantes pour pouvoir le résoudre (aucune solution ou problème impossible) (Kitchner, 1983). Le problème à diverses interprétations est un problème suscitant différentes visions possibles du problème menant à différentes réponses possibles. Enfin, le problème contextualisé est celui qui se présente dans des situations réelles tirées de la vie sociale d’un jeune ou d’un adulte ou dans des situations fictives. Le schéma conceptuel présenté à la figure 1 représente la vision du problème mathématique riche adoptée pour cette étude. Dans ce schéma, les rectangles représentent les cinq caractéristiques retenues dans la définition du problème mathématique riche, tandis que les bulles correspondent aux critères observables dans les énoncés des problèmes écrits.

Figure 1 • Schéma conceptuel du problème riche (conçu par Manuel, 2010)

Depuis l’arrivée des TIC (Technologies de l’Information et de la Communication) dans les écoles munies d’un accès Internet haute vitesse (parfois sans fil), une multitude de ressources éducatives deviennent disponibles gratuitement. Il serait donc raisonnable de s’attendre à leur impact sur les pratiques courantes en salle de classe et au-delà. Selon Klotz (Klotz, 2003), l’expansion des outils technologiques comme les communautés d’apprentissage et de collaboration sur le Web modifie le concept de la salle de classe, car non seulement ces outils influencent ce qui est appris, mais aussi comment les concepts sont appris. Ceci par conséquent influence les relations entre les enseignants et les élèves, car ces communautés offrent une panoplie d’activités amusantes comprenant des défis que les enseignants peuvent proposer à leurs élèves afin de différencier les apprentissages et ainsi mieux répondre à leurs besoins particuliers. L’historique de la communauté CAMI que nous analysons dans la section suivante démontre que la création de problèmes riche au sens de Manuel et al. (Manuel et al., 2012) présente des défis de taille sur le plan technopédagogique et nécessite une collaboration soutenue entre les pédagogues, les didacticiens, les programmeurs et les utilisateurs (enseignants et élèves).

3. Historique et aperçu global de la communauté virtuelle CAMI : quel apport à l’apprentissage ?

En faisant part de l’évolution des espaces numériques de travail en mathématiques, Kuntz (Kuntz, 2007) analyse la ressource virtuelle Mathenpoche qui propose, à l’intérieur même du logiciel, un tableur, un traitement de textes mathématiques, un traceur de courbes et un logiciel de géométrie dynamique. Selon l’auteur, plusieurs aspects du travail de l’élève dans un tel environnement doivent être examinés tels que la façon d’enrichir et d’ouvrir les exercices un peu fermés, la complémentarité de l’espace virtuel en rapport avec les environnements d’apprentissage plus traditionnels, le savoir que l’élève peut acquérir dans un tel espace et les moyens d’évaluer ce qu’apprennent les élèves dans ces conditions (Kuntz, 2007).

L’apport des technologies de l’information et de la communication (TIC) pour soutenir la résolution de problèmes a été étudié entre autres par Hersant (Hersant, 2003) qui a analysé l’utilisation d’un logiciel associé à une banque de problèmes structurés qui propose des problèmes de proportionnalité. Dans cet environnement, les problèmes sont donc le lieu de mise en fonctionnement des connaissances de l’utilisateur, tandis que les messages et explications permettent l’apport de connaissances aux utilisateurs, en essayant de s’adapter aux erreurs effectuées, identifiées à l’aide d’une analyse a priori (Hersant, 2003).

Au cours de la dernière décennie, le contexte d’utilisation des TIC à des fins éducatives a été enrichi par le concept de communautés de pratiques issu des travaux de Wenger (Wenger, 1998). Grosjean (Grosjean, 2007) justifie une application de ce concept dans un contexte d’une communauté virtuelle qui semble avoir des dimensions limitées à une situation formelle d’un cours à distance. L’auteure soutient toutefois que l’existence d’une communauté virtuelle d’apprenants dans ce contexte est dépendante des processus de négociation et de construction collective de sens qui vont s’accomplir et des référents communs que les participants vont partager. Un lien étroit entre les travaux de Wenger (Wenger, 1998) et le cadre de recherche instrumentale de Rabardel (Rabardel, 1995) a été faite par Sokhna et Dia (Sokhna et Dia, 2009) qui arriment l’idée de médiation, la distinction entre l’artefact et les instruments et la non-permanence de l’instrument avec ceux des communautés de pratiques, soit le concept d’une ressource pédagogique élaborée « n’est pas seulement pour prendre en compte les types d’utilisation des ressources, mais pour faire vivre les outils et favoriser le travail collaboratif entre pairs » (Sokhna et Dia, 2009), p. 6.

En mathématiques, on trouve des exemples de communautés virtuelles d’apprentissage qui semblent avoir démontré leur potentiel d’appuyer la construction des connaissances par les élèves, souvent, en collaboration avec leurs pairs. Renninger et Shumar (Renninger et Shumar, 2002) analysent le site Math Forum (www.mathforum.org) qui offre un environnement dans lequel les participants interagissent ensemble afin de générer de façon collaborative des services et des ressources, de bâtir une fondation de construction de nouvelles connaissances en mathématiques, en pédagogie, en technologie et encore plus, d’instaurer une culture mettant l’accent sur les habiletés à poser et à résoudre un problème. Cette complexité d’interactions générée par l’environnement virtuel peut amener des apprentissages de haut niveau cognitif allant au-delà d’une triade « question – réponse — rétroaction ». À leur tour, les chercheurs étudiant le site Internet NRICH (http://nrich.maths.org/frontpage) expriment leur conviction par rapport à la résolution de problèmes comme processus créatif qui est à la base des mathématiques comme activité humaine (Piggott, 2007)

Pallascio (Pallascio, 2003) a étudié un autre type de communauté virtuelle de recherche nommée l’Agora de Pythagore (http://euler.cyberscol.qc.ca/pythagore/). Cet environnement propose aux élèves des situations d’apprentissage dans lesquelles les participants peuvent philosopher sur différents sujets de nature épistémologique complexe (comme, par exemple, le concept de l’infini). Dans ce contexte de débat philosophique, les élèves deviennent les acteurs et les créateurs de leurs propres connaissances par l’entremise de discours argumentatifs (Pallascio, 2003). Le concept de la communauté virtuelle d’apprentissage y apporte, selon l’auteur, une nouvelle dimension didactique permettant d’aller au-delà de la perception de l’élève comme acteur ou un être actif dans son processus d’apprentissage, mais de le considérer comme auteur ou producteur de ses connaissances. Taurisson (Taurisson, 2003) va même plus loin en amenant la métaphore d’une « explosion du triangle didactique » qui sera remplacée par une structure dynamique et complexe avec multiples interactions qui développent de nouvelles propriétés qui évoluent constamment et qui autocorrigent le fonctionnement du processus d’enseignement-apprentissage. Selon le même auteur, le monitorage de l’évolution de ces systèmes complexes fait intervenir les chercheurs « modérateurs » qui veillent à ce que le développement soit cohérent et poursuit les buts fixés (Taurisson, 2003).

La première version du site Internet nommée Chantier d’apprentissages mathématiques interactifs (CAMI) a été lancée en septembre 2000, avec la collaboration de l’Université de Moncton et du District scolaire 1 du Nouveau-Brunswick (Vézina et Langlais, 2002). Le but de ce projet était, dans un premier temps, de créer un outil pour aider les élèves francophones du Nouveau-Brunswick à développer des habiletés en résolution de problèmes et en communication d’idées mathématiques, et dans un second temps, de se servir de cet outil pour former les étudiants en didactique des mathématiques à l’Université de Moncton. Ce second but permettait à la cohorte universitaire de pouvoir mieux comprendre les raisonnements utilisés par les élèves dans un processus de résolution de problèmes, de développer des habiletés en évaluation formative et de se familiariser au rôle des technologies comme outil d’apprentissages en mathématiques (Vézina et Langlais, 2002).

Le modèle du problème de la semaine (Problem of the Week) exploité par l’équipe du site Math Forum cité ci-dessus (Renninger et Shumar, 2002) a été retenu. Sur une base hebdomadaire, quatre problèmes mathématiques étaient affichés sur le site CAMI selon quatre niveaux de difficulté (apprenti, technicien, ingénieur et expert). Vers la fin de 2005, cette communauté virtuelle émergente donnait l’accès à une base de plus de 700 problèmes mathématiques dans les domaines de nombres et opération, régularités et relations, formes et espace, ainsi que l’analyse de données et probabilités (Freiman et al., 2005a). Selon les résultats de premiers sondages réalisés par l’équipe CAMI, les élèves ont dit avoir aimé le design du site et les activités de résolution de problèmes en ligne. Les enseignants, à leur tour, semblaient avoir apprécié les occasions d’améliorer les habiletés en résolution de problèmes et en communication mathématique chez leurs élèves. Les étudiants en formation initiale disent avoir aimé l’occasion de pouvoir analyser les solutions authentiques des élèves et de leur rédiger des rétroactions formatives (Vézina et Langlais, 2002) ; Freiman et al., 2005b).

Ces mêmes sondages indiquaient toutefois des limites importantes de la communication par courriel qui était parfois instable et peu efficace. Les traces du travail des élèves se perdaient dans une multitude de messages non structurés. La logistique du site ne permettait pas, non plus, de suivre les progrès des élèves (sous forme d’un portfolio électronique), un besoin clairement exprimé dans les sondages.

Avec le nouveau site CASMI qui fut officiellement lancé en 2006, l’utilisateur devenait membre de la communauté en se créant un profil d’utilisateur et en obtenant ainsi une possibilité de gérer son propre portfolio nommé Mon dossier en y accédant avec un mot de passe et un nom d’utilisateur. Dans ce dossier, toutes les traces du travail accompli par l’utilisateur étaient conservées dans la base de données dynamique, c’est-à-dire les problèmes résolus, les rétroactions formatives personnalisées reçues, et les problèmes qu’il a proposés. Dans cette même rubrique, l’utilisateur pouvait modifier les informations contenues dans son profil et peut aussi partager son dossier avec tout autre membre de la communauté en utilisant le nom identifiant : un nom (code) unique attribué à chaque membre de la communauté.

Une analyse détaillée des cadres théoriques et méthodologiques de la conception de la communauté CASMI a été présentée dans Freiman et Lirette-Pitre (Freiman et Lirette-Pitre, 2009a). Notons ici qu’au niveau technologique, le site constituait une plate-forme virtuelle munie d’une structure dynamique de base de données COLD FUSION. Cette nouvelle conception du site a permis d’améliorer les interactions entre le système de gestion des données et les utilisateurs et aussi entre les utilisateurs. De plus, il est devenu possible d’enregistrer, de stocker et d’utiliser les différentes traces numériques d’usage grâce aux divers outils d’interaction et de communications asynchrones implantés, ce qui a généré plus de 30000 solutions d’élèves soumises à un total de 400 problèmes, pour une période entre le mois de septembre 2007 et le mois de mai 2010, comme résultats de plus de 100000 visites de plus d’un million des pages visionnées.

La section de mathématiques au sein de la communauté CASMI a été élargie en incorporant également des questions du domaine des sciences (physique, chimie et biologie), ainsi que des énigmes d’échecs (Freiman et al., 2007). En 2010, le site est devenu multidisciplinaire en abritant maintenant les sections de littératie (développée par Sylvie Blain, professeure à l’Université de Moncton) et de sciences humaines (développée par Aicha Bennimas, également professeure à l’Université de Moncton). Le site a ainsi retrouvé son abréviation initiale CAMI qui signifie maintenant Communauté d’apprentissages multidisciplinaires interactifs. Déjà en collaboration avec l’Association Sésamath depuis 2008 permettant un pont virtuel avec leur ressource Mathenpoche, le site donne également aux membres de la communauté un accès direct au Marathon virtuel des mathématiques, un nouveau site bilingue (http://www8.umoncton.ca/umcm-mmv/index.php), étant le produit d’une collaboration internationale (Freiman et Appelbaum, 2011).

Néanmoins, la section Problème de la semaine en mathématiques demeure le noyau de la communauté dont les membres résolvent les problèmes par l’entremise d’un formulaire contenant différents outils de communication. Semblable à la barre d’outils que l’on retrouve dans les logiciels de traitement de texte, le membre peut ajouter des images, utiliser les émoticônes, choisir les couleurs, la police, ajouter des liens hypertextes et peut même créer des fichiers audio et vidéo et les ajouter dans sa solution. Les étudiants universitaires, lors de leur formation en didactique, peuvent ainsi accéder aux solutions des élèves et les analyser de plusieurs façons en vivant ainsi une expérience plus authentique (Freiman, 2010). En plus d’un profil personnel protégé par un mot de passe, cet environnement virtuel donne l’accès à tous les utilisateurs à un espace des ressources partagées telles qu’une banque des problèmes archivés et des commentaires généraux portant sur l’ensemble des solutions pour chaque problème. Un forum de discussion a aussi été instauré afin que les membres puissent communiquer et partager avec tous les autres membres de la communauté (Freiman et Lirette-Pitre, 2009b).

Les traces numériques d’usage laissées par les membres de la communauté ainsi que les données des sondages et des entrevues nous ont permis d’entamer des analyses plus profondes pour évaluer le potentiel éducatif du site sur l’enrichissement en mathématiques (Freiman, 2009), la créativité mathématique (Manuel, 2010), les difficultés des élèves (Pelczer et Freiman, 2009) et les défis de formation des maîtres qui donnent une rétroaction formative à l’élève (Leblanc et Freiman, 2011).

Toujours dans le but d’éclairer l’impact du site sur les apprentissages, nous avons interrogé des élèves de trois écoles qui ont travaillé sur le site CASMI (nous utilisons cet acronyme pour le reste de notre texte, car les données analysées se rapportent à cette étape de développement de la communauté virtuelle) de façon régulière pendant deux années, ainsi que leurs enseignants en demandant de quelle manière leur participation affecte leurs perceptions par rapport aux mathématiques en général et aussi par rapport à la résolution de problèmes. Par la suite, nous analysons les traces de solutions des élèves pour comprendre comment les élèves communiquent leurs démarches à partir d’une démarche authentique construite par l’élève. Les deux prochaines sections discutent des thèmes ressortis des entrevues semi-dirigées et une diversité des solutions des élèves communiquées de différentes façons à l’aide des outils technologiques (traitement de texte) et des raisonnements logico-mathématiques (registres et relations).

4. Perceptions des élèves et des enseignants par rapport à la ressource et aux nouvelles occasions d’apprentissage

Les perceptions des élèves et des enseignants ont été recueillies lors des ateliers de présentation du site dans trois écoles francophones du Nouveau-Brunswick. Ces écoles choisies faisaient partie d’un projet pilote géré par le ministère de l’Éducation du Nouveau-Brunswick dans le cadre duquel tous les élèves de 7e et 8e année ainsi que les enseignants avaient l’accès direct à un ordinateur portatif (Fournier et al., 2006). Ainsi, nous avons fait des entretiens de groupe (à la fin des ateliers) et individuels, de 15-20 minutes, avec 8 élèves (4 garçons et 4 filles âgés de 13-14 ans) et trois enseignants. Les questions posées touchaient la participation au projet, les impressions du site (design et activités), l’impact en général sur l’apprentissage de la résolution de problèmes et des mathématiques. Les entretiens ont été audio-enregistrés, transcrits et analysés par une double lecture par les chercheurs et une discussion d’interprétation et de validation.

Les points suivants ont été ressortis lors de discussions en groupe-classe :

Par rapport au design global du site, les participants ont exprimé leur satisfaction générale (nous citons ici les paroles des élèves transcrits du verbatim des ateliers). Entre autres, ils ont mentionné que « le site est vraiment beau et attrayant», fait avec une technologie de pointe (Le site est vraiment « high tech » ; c’est le meilleur site que je n’ai jamais vu). Les personnages du site semblent plaire aux élèves (La mascotte est « cute » ; les images sont belles et c’est intéressant avec les animaux). Par rapport au contenu, les élèves semblent avoir apprécié « le fait qu’on a les sections sciences et échec est déjà un gros plus ». Le contenu leur semble également pertinent et complet (C’est très bien. Vous avez tout mis).

Par rapport aux outils technologiques, les élèves ont fait allusion au forum de discussion comme moyen de communication avec d’autres élèves (C’est cool qu’on a un « chat » qui nous permet d’aller consulter les élèves d’autres écoles si on a des problèmes), l’avantage d’avoir son propre compte pour garder toutes les traces du travail (Le fait qu’on a notre propre compte ; C’est excellent le fait qu’on a chacun un compte, car comme ça, on peut revoir ce qu’on a fait et on ne perd rien, même pas nos solutions) et finalement le plaisir d’avoir une variété d’outils de rédaction incluant une possibilité de faire des dessins (C’est le « fun » avec les outils. On peut faire des dessins).

Après avoir analysé les verbatim des entrevues individuelles, nous avons ressorti sept principaux thèmes :

Thème 1 : Le développement du sens d’autonomie et de débrouillardise

Les problèmes posés sur le site CASMI semblent pousser les élèves à se débrouiller davantage en trouvant des stratégies ou des informations technologiques ou mathématiques nécessaires pour résoudre les problèmes.

Selon les entrevues, l’accès à Internet permet aux élèves de faire des recherches rapides pour des informations ou des outils qu’ils ne connaissent pas, ce qui n’est pas toujours possible à l’aide d’un manuel. En plus de pouvoir apprendre de nouvelles fonctions technologiques, les élèves ont eu l’accès instantané à une vaste gamme d’informations touchant les contenus mathématiques. Un élève a ainsi affirmé : « Je peux chercher sur Internet pour des choses que je ne sais pas ».

Du côté des enseignants, ces mêmes observations ressortent également. Un enseignant a remarqué, entre autres :

« Les élèves sont ingénieux. Ils se trouvent des manières pour résoudre les problèmes. Dans un cas, ils devaient faire un dessin, mais le site CASMI ne le permettait pas. Alors, ils se sont débrouillés. Ils l’ont placé sur leur cybercarnet et ont fait un lien à leur cybercarnet ».

Les élèves ont, alors, fait des liens entre différents outils informatiques.

Un autre enseignant a partagé le cas d’un élève qui a réussi à résoudre un problème avec la notion du théorème de Pythagore, un concept qu’il n’avait pas appris auparavant : « Un élève de 7e qui devait appliquer le théorème de Pythagore pour résoudre un problème, il ne l’avait pas appris. Il a fait une recherche dans Internet et par la suite, il a présenté le théorème aux autres élèves de la classe ».

Les enseignants ont aussi exprimé une grande satisfaction par rapport à l’autonomie que les élèves avaient développée avec le site CASMI en mentionnant que les élèves les consultaient de moins en moins lorsqu’ils étaient sur le CASMI vers la fin de l’année : « Au début de l’année, j’étais beaucoup consulté par les élèves pour les aider à résoudre les problèmes. Mais, plus on avançait, plus ils se débrouillaient et consultaient les autres ».

Le développement d’un sens d’autonomie ainsi observé dans un environnement doté d’un accès à des outils technologiques en mathématiques est un phénomène intéressant. Sabra et Trouche (Sabra et Trouche, 2009) ont effectué des analyses de plusieurs recherches didactiques en mathématiques et ont remarqué que :

« dès que l’apprenant dispose des outils nécessaires à son apprentissage (des ressources pédagogiques, des outils technologiques différents : calculatrices, logiciels), et dans la mesure où la tâche est bien adaptée à ses possibilités et ses besoins, l’interaction “apprenants-ressources” manifeste cette autonomie dans un milieu organisé dans le but d’atteindre les objectifs didactiques de cette activité » (Sabra et Trouche, 2009), p. 64.

Thème 2 : Motivation face aux défis intellectuels 

La communauté virtuelle CASMI semble augmenter les occasions de résolution de problèmes à l’aide des défis posés régulièrement tout en motivant les élèves. Tout d’abord, les sujets mentionnent que les problèmes posés sur la CASMI offrent de bons défis intellectuels, ce qui amène les élèves à bien réfléchir pour les relever. Selon les entrevues, les élèves semblent être motivés par les défis que les problèmes leur apportent. Ils savent que certains problèmes sont faciles, mais d’autres sont plus difficiles à résoudre. Effectivement, un élève a partagé : « J’aime les problèmes, car ils te font penser. Ils sont des défis, car ils ne sont pas tous faciles à résoudre. Un problème c’est un problème ». Un autre élève abonde dans le même sens : « Il faut beaucoup penser pour résoudre les problèmes. Certains sont faciles, mais d’autres sont très difficiles ».

De plus, malgré les défis à relever, les élèves semblent être plus motivés à résoudre les problèmes en ligne comparativement aux manuels de mathématiques en format papier. Un élève affirme : « plus on pratique, mieux on devient... C’est plus motivant de faire un problème sur le site que dans un livre. C’est moins intéressant de résoudre un problème d’un livre de 1970 ». Un élève en particulier a mentionné aussi qu’il n’utilisait pas le site seulement à l’école. Il dit : « Je vais résoudre des problèmes à la maison parfois ».

Les enseignants avancent, à leur tour, que le site contient une bonne variété de problèmes complexes qui respectent les contenus des programmes d’études et qu’ils n’ont pas besoin de motiver les jeunes pour consulter le site. Un enseignant mentionne : « Moi j’adore le site CASMI. Ce n’est pas monotone et les problèmes touchent à tous les objectifs du programme d’étude... Bonne complexité et variété dans les problèmes... Pas besoin de motiver les jeunes pour aller sur le site ».

Ce rapport didactique entre le défi qu’offre la résolution de problèmes et la construction de nouvelles connaissances mathématiques a été observé par Poirier (Poirier, 2001), p. 5 : « S’il n’y a pas de problème à résoudre, de défi à relever, il n’y aura aucune motivation à construire de nouvelles connaissances ».

En plus de voir de nouvelles options didactiques, les enseignants rapportent une satisfaction qu’ils observent chez leurs élèves par rapport à leurs succès. Les enseignantes mentionnaient également que les élèves leur montraient leurs solutions. Un enseignant en particulier dit : « Les élèves viennent souvent me montrer leurs solutions et leurs rétroactions. Regarde madame, j’ai résolu le problème ». Un enseignant nous a mentionné que certains élèves ne se contentent pas d’avoir résolu un problème, ils commencent à se chercher aussitôt d’autres défis : « Cet élève en particulier qui n’en a pas assez des maths, il avait du plaisir à essayer les problèmes experts (les plus difficiles) et de me dire qu’il avait trouvé la bonne réponse. C’était plaisant m’asseoir avec lui et voir ses façons de penser ».

Cet engagement dans une activité mathématique enrichie et authentique a été observé par d’autres chercheurs, comme le rapporte Piggott (Piggott, 2007) :

« When engaging in enriching mathematical activities, learners are drawn into the mathematics either because of the context or the mathematics that emerges from the problem itself. Contexts may result in learners initially experiencing a sense of slight unease. However, through such experiences, the aim is for learners develop as confident and independent, critical thinkers. Learners should be encouraged to be creative and imaginative in their application of knowledge » (p. 38).

Les enseignants semblent être satisfaits de la qualité des problèmes qui sont posés sur le site CASMI. Ceci facilite leur recherche de bons problèmes. Et de plus, étant donné que ce sont les étudiants en formation des maîtres qui font les rétroactions, les enseignants n’ont pas besoin d’en faire la correction. Un enseignant résume ces points en disant : « Je n’avais pas besoin de chercher pour de bons problèmes. Et de plus, pas besoin de faire la correction, car les élèves recevaient une rétroaction plus détaillée que ce que l’on donne ».

Thème 3 : Évaluation formative et nouveaux types d’interaction 

Les participants semblent apprécier les rétroactions formatives personnalisées que les élèves reçoivent. Les examens provinciaux en mathématiques organisés par le ministère de l’Éducation du Nouveau-Brunswick à la fin de la 3^e, de la 5^e, de la 8^e et de la 11^e années selon le cadre d’évaluation cohérent avec les principes didactiques mentionnés dans nos sections précédentes mesurent, entre autres, les habiletés des élèves à gérer et résoudre une situation-problème, à raisonner et communiquer mathématiquement et à faire des liens (MENB, 2008). L’accent placé sur la résolution de problèmes dans un environnement virtuel permet aux enseignants d’avoir une rétroaction diagnostique utile pour améliorer l’enseignement axé sur la compréhension plus profonde de contenus mathématiques par les élèves, ainsi qu’une meilleure maitrise d’habiletés et d’usage, productive de méthodes d’apprentissage et de la pensée. Un tel outil d’évaluation devrait non seulement mesurer les résultats d’apprentissage, mais également le processus et les stratégies (De Corté et Masui, 2008).

Selon les entrevues, les élèves semblent apprécier le fait que ce sont des étudiants du niveau universitaire qui leur donnent une rétroaction sur leurs solutions. Le travail effectué par les étudiants en formation des maîtres semble être valorisé par les élèves. Les élèves mentionnent qu’ils aiment recevoir les rétroactions de leurs solutions. De plus, ils semblent être motivés de recevoir une rétroaction d’une autre personne que leur enseignant. Et aussi, ces rétroactions sont faites par des personnes qui sont quand même adultes. Un élève trouve que : « C’est excellent qu’on a quelqu’un qui nous corrige et nous envoie des commentaires ».

Ces rétroactions leur permettent de se corriger et d’améliorer leurs habiletés en résolution de problèmes. Un élève a dit : « Je trouve que les rétroactions sont claires. Ça nous montre nos fautes, ce qu’on fait bien et ce qu’on peut faire mieux la prochaine fois ».

Selon les enseignants, le site leur permet de réviser des notions mathématiques à travers la résolution de problèmes, ce qui amène l’élève à puiser dans ses connaissances antérieures. Un autre constat : même si ce dernier n’enseigne plus ce module quand un problème est posé, il peut l’utiliser comme évaluation formative afin de voir si les élèves maîtrisent encore les concepts vus antérieurement, ou encore, s’il fallait expliquer ou réexpliquer certains concepts. Un enseignant résume : « Même si je n’étais pas dans mon module de géométrie et qu’un problème de géométrie était affiché, les élèves devaient aller dans leurs connaissances antérieures et trouver des méthodes pour le résoudre. Et à certaines occasions, je devais expliquer un petit concept ».

Les enseignants semblent aussi être satisfaits de la qualité ainsi que de la rapidité des rétroactions qui sont données aux élèves qui résolvent les problèmes. Un enseignant dit : « Je sais qu’il y a d’autres sites de ce genre sur le web. Mais j’n’en ai pas trouvé un où l’interaction se fait aussi vite comme CASMI ». Les enseignants semblent aussi observer la fierté que les élèves ont du fait qu’ils reçoivent une rétroaction d’un étudiant de l’Université de Moncton. Un enseignant a mentionné : « Le fait que les élèves sont au courant que quelqu’un corrige sa solution et qu’ils reçoivent un feedback, je crois que ça fait la magie du jeu ». Le fait de ne pas avoir un feedback immédiat va en quelque sorte à l’encontre de la culture de jeux dans les environnements virtuels auxquels les jeunes semblent être habitués, selon Gadanidis (Gadanidis, 2001). Selon l’auteur, une rétroaction asynchrone peut ajouter plus de profondeur dans les apprentissages à long terme et de meilleure qualité (Gadanidis, 2001).

D’autres aspects peuvent être également mis en valeur, comme, par exemple, le sentiment de réussite. Là-dessus, les enseignants ont mentionné que les élèves sont fiers de leur montrer leurs rétroactions. Voici les propos d’un enseignant en particulier : « Les élèves ont le plaisir de nous montrer les rétroactions qu’ils reçoivent. Regarde monsieur, je l’ai bien fait le problème ».

Thème 4 : Occasions de partage et de collaboration entre les élèves

Le site CASMI semble stimuler des discussions, des partages et des échanges entre les élèves en salle de classe. Selon les entrevues, les élèves mentionnent qu’ils ont plus tendance à collaborer avec les autres camarades de classe et discuter des problèmes et de différentes stratégies possibles pour les résoudre, voire même s’entraider. Un élève en particulier a mentionné que : « Si je ne peux pas résoudre un problème, je vais voir des amis pour m’aider ».

Les enseignants ont fait la même remarque que les élèves. Tous les enseignants ont mentionné que les élèves aiment discuter des problèmes posés sur le site CASMI. Un enseignant décrit ce climat de la façon suivante : « C’est comme s’ils avaient gagné un trophée ». Un autre enseignant a aussi mentionné à nouveau le fait que les élèves avaient plus tendance à se regrouper ensemble pour travailler un problème. Il a mentionné : « Pour le problème des patates de tout à l’heure, quelques élèves étaient sur la bonne piste et se sont regroupés pour s’entraider. Copier ? NON ! Collaborer et expliquer OUI ! ... et je n’avais pas besoin d’être la personne ressource ». Ainsi, nous pouvons conclure que le CASMI semble apporter des occasions de collaborer et de travailler en groupes. Ces occasions d’échanges semblent donc se multiplier avec les technologies.

Les autres recherches semblent confirmer que les discussions émergent plus facilement autour de problèmes riches dans une atmosphère où chaque contribution est valorisée et les élèves apprennent à écouter leurs pairs (The Math Forum's Bridging Research and Practice Group, 2000).

Thème 5 : Différenciation des apprentissages 

Le CASMI semble respecter une pédagogie différenciée en ce qui concerne les habilités des élèves et leur rythme de travail en permettant de faire des choix. En lien avec la pédagogie différenciée prônée par les programmes d’études au Nouveau-Brunswick (MENB, 2005), le site semble permettre d’enrichir ou de modifier les attentes à l’intention d’un petit nombre d’élèves qui présentent des forces ou des défis cognitifs particuliers. Dans une entrevue, un élève mentionne : « Si je ne peux pas résoudre le problème, j’en essaie un autre. Parfois, le problème du niveau 3 est trop difficile pour moi, alors je vais faire un plus bas ». Dans une seconde entrevue, un autre élève mentionne : « Je regarde les problèmes et je fais ceux que je suis capable de faire ». Ces deux citations semblent démontrer que les élèves peuvent choisir de leur propre gré les problèmes qu’ils sont plus aptes à résoudre. Pour les élèves plus faibles en mathématiques, ils peuvent tenter de résoudre les problèmes les plus faciles, tandis que les élèves plus forts peuvent tenter les plus difficiles.

Les enseignants semblent tenir les mêmes propos. Un enseignant remarque que : « Chaque élève avance à son propre rythme ». Un autre enseignant reconnaît la pertinence d’avoir quatre catégories de problèmes établies selon le niveau de difficulté. Il mentionne : « Puisqu’il y a les niveaux, les élèves plus faibles peuvent faire les niveaux plus bas et les plus forts les niveaux plus élevés ».

Les propos des participants semblent refléter différentes formes de différenciations facilitées par les TIC : par tâche, par réponse, par support et par ressource (Kennewell, 2004).

Thème 6 : Différentes stratégies et différentes solutions 

Le site CASMI semble favoriser le développement du raisonnement et de la communication mathématique, car il est ouvert à une variété des approches et des outils utilisés par les élèves. Les élèves mentionnent que le site les pousse à développer leurs habiletés en communication mathématique. Afin que les assistants qui rédigent des rétroactions pour les élèves puissent mieux comprendre leurs solutions, ils doivent ajouter plus de détails comparativement au contexte de la salle de classe. Un élève confirme cet aspect en soulignant : « Le site m’amène à écrire plus de phrases et des phrases complètes ».

Les enseignants ont aussi remarqué les possibilités que le site CASMI ouvrait à la communication mathématique. Ils jugent que cette habileté n’est pas très développée dans la salle de classe. Ils trouvent donc le site CASMI très bénéfique pour aider au développement de cette habileté. Une enseignante en a discuté longuement en mentionnant que : « La communication mathématique est un gros problème dans les écoles de la région. Mais il y a eu une progression. Les élèves sont plus capables de s’exprimer, de donner leur propre version du problème, leur stratégie, pas juste la réponse. ... Les élèves doivent s’exprimer à quelqu’un qui n’est pas présent dans la classe. ... Le langage mathématique améliore aussi ».

Les échanges et les discussions en classe, ainsi que le partage de solutions exemplaires dans l’espace virtuel commun du site semblent favoriser la communication tout en permettant aux élèves d’apprendre sur les stratégies des autres. Un élève le mentionne : « Pas tout le monde résout le problème de la même manière. C’est intéressant de voir ce que les autres font ».

Des propos similaires proviennent des enseignants. Citons les trois commentaires suivants : « Les solutions exemplaires et le reste sont bien structurés. On peut voir les différentes façons que les élèves s’y prennent pour résoudre le problème » ; « Tout raisonnement permet de développer la logique et même la pensée critique »; et : « J’étais surpris de voir des élèves trouver des raisonnements différents que les miens. Souvent, je n’y pensais même pas à cette façon ». Ces commentaires semblent confirmer que, non seulement les problèmes posés sur le site CASMI offrent une ouverture aux différentes stratégies et aux différents raisonnements mathématiques, ils ouvrent aussi la voie au développement d’autres habiletés telles que la pensée critique et même créative, une qualité dont les bénéfices sont bien documentés dans les travaux de Leikin par exemple (Leikin et al., 2006).

Cette ouverture peut contribuer, selon les chercheurs, à un climat de confiance propice aux apprentissages réussis tout en sollicitant les perspectives et les approches multiples en résolution de problèmes (Zodik et Zaslavsky, 2004).

Thème 7 : Satisfaction personnelle et confiance par rapport à la résolution des problèmes mathématiques

La pratique sur le site CASMI semble augmenter la confiance chez les élèves et ces derniers voient les mathématiques plus positivement.

Parmi d’autres commentaires, les élèves ont mentionné que résoudre les problèmes sur le site leur apporte une plus grande confiance quant à leurs habiletés à résoudre des problèmes mathématiques. De plus, le site CASMI semble permettre aux élèves de ressentir une satisfaction personnelle quant à leur performance en résolution de problèmes. Un élève en particulier parlait de son expérience d’avoir travaillé fort pour résoudre un problème en particulier, et, après quelques jours, l’a réussi. Il était aussi fier de voir son nom parmi la liste de ceux et celles qui avaient réussi à résoudre ce problème. Il rapporte : « J’étais le seul de la classe à résoudre le problème des personnes et les animaux. Mais ça m’a pris 4 à 5 jours... C’est le fun de voir notre nom sur le site qu’on a eu la bonne réponse ».

Les élèves ont également témoigné de leurs progrès d’une semaine à l’autre dans leurs apprentissages en mathématiques ainsi qu’en leurs habiletés en résolution de problèmes. Certains ont même développé une meilleure attitude à l’égard des mathématiques et sont maintenant plus confiants. Quelques commentaires émis par les élèves pour appuyer ces points sont les suivants : « Je suis plus confiante en math maintenant, car je pratique plus » ; et « Avant, moi, les maths, ça n’allait pas. Mais maintenant, ça va beaucoup mieux avec le CASMI ». Aussi, les élèves ont souligné qu’avec la pratique sur le site, ils sont devenus plus confiants à résoudre des problèmes et ils le font avec moins d’aide de la part de leurs enseignants. Un élève a mentionné : « Si je ne pouvais pas résoudre le problème, je demandais de l’aide à mes amis ou je cherchais dans Internet ».

Les enseignants ont aussi observé une amélioration au niveau des apprentissages en mathématiques chez leurs élèves, grâce à la pratique sur le site CASMI. Un enseignant a conclu que : « Ce qui était difficile pour un élève au début de l’année ne l’est plus à la fin ».

Ces observations semblent s’aligner avec les travaux des chercheurs qui démontrent le rôle prédominant des enseignants dans le développement des attitudes positives chez les élèves face aux mathématiques : « Teachers should encourage students to realize self-efficacy, self-esteem and self-respect because these factors help students gain higher achievement motive and if the students have high achievement motive, they will have good attitude toward learning, then they will concentrate on learning and they will be efficiently successful in studying as they expect» (Pimta et al., 2009), p. 384.

5. Communication de la démarche de résolution de problèmes dans un environnement virtuel : parler mathématique à l’aide des TIC

Dans l’espace virtuel, les élèves se trouvent aux prises avec des problèmes mathématiques, l’activité dans laquelle la validation et la communication de la démarche deviennent donc des éléments importants de la résolution de problème (Poirier, 2001).

Bien qu’il existe différentes options de formats de présentation de problèmes dans l’interface utilisateur du site (texte ou lien vers un fichier audio ou vidéo), la grande majorité de nos énoncés sont présentés sous forme textuelle accompagnée d’une illustration qui est liée au contenu du problème. Cet énoncé s’ouvre dans une fenêtre de travail de résolution du problème suivi d’un formulaire électronique vierge qui contient des outils standards de traitement de texte (polices, couleurs, taille, insertion des liens et d’images, puces, tableaux et autres). Le choix de moyens de représentation appartient donc à l’élève et nous pouvons nous attendre à une grande variété de formats. Cette variété de moyens « virtuels » est jumelée avec une variété de représentations proprement mathématiques, ce qui crée un environnement technopédagogique différent de celui en format papier et crayon. Ce nouveau type d’environnement numérique mérite d’être examiné avec plus de profondeur. À titre d’exemple, nous avons choisi le problème suivant :

L’énoncé a été accompagné d’une photo de l’horloge (voir le lien pour l’énoncé.

http://www2.umoncton.ca/cfdocs/cami/cami/cami.cfm?action=
PreviewPbArchive&IDS=135&V_Categ=MT&IMG=TEC&IDPROB=1057).

Selon les critères de richesse définis par Manuel (Manuel, 2010) - problème ouvert, contextualisé – ce problème a été classé comme moyennement riche. Il fait appel à des concepts et à des structures mathématiques déjà connus par l’élève (comme, par exemple, la notion de l’angle et de sa mesure) et d’autres qui peuvent être mobilisés par l’élève (exemple, un raisonnement proportionnel) en lui permettant d’élaborer différentes stratégies menant à une variété de réponses. Bien qu’il existe une formule directe permettant de calculer la mesure de l’angle en degrés (exemple, http://en.wikipedia.org/wiki/Clock_angle_problem), nous nous attendions à ce que l’élève connaisse la formule et donc qu’il s’engage dans son propre processus de construction de la démarche de résolution. Dépendamment de son interprétation de l’énoncé, l’élève pouvait ainsi définir sa tâche comme celle de trouver le type de l’angle (obtus ou aigu) ou comme celle de calculer (estimer) la mesure de l’angle entre les aiguilles. Ainsi, les élèves pouvaient répondre que c’est un angle obtus (si l’on regarde l’angle dans le sens de l’aiguille) ou un angle rentrant (si l’on considère l’angle dans le sens antihoraire). D’autres élèves pouvaient aussi entreprendre une démarche plus rigoureuse (et pédagogiquement plus souhaitable) en calculant la mesure de l’angle en degrés, à partir de relations entre les données (exemple, entre l’unité de temps et l’angle). Pour des élèves du secondaire, la mesure de l’angle pouvait être exprimée en radians.

Au niveau des représentations, l’élève pouvait utiliser l’horloge comme matériel de manipulation et utiliser un rapporteur pour mesurer l’angle. L’élève pouvait aussi faire un dessin d’une horloge (image) et par la suite, estimer l’angle (voir la Figure 2. Notez que nous conservons dans les citations d’exemples et dans les figures suivantes le texte tel qu’écrit par l’élève, tout en conservant son langage authentique), mesurer l’angle à l’aide du rapporteur ou le déterminer à l’aide de calculs.

Figure 2 • Dessin et estimation

En analysant l’espace virtuel collectif de solutions, terme introduit par (Manuel, 2010) de ce problème comportant 73 solutions, nous avons pu faire quelques observations par rapport à la communication mathématique (variété des expressions décrivant les relations mathématiques et des raisonnements sous-jacents). Nous avons également observé des expressions faisant ressortir des émotions ou des relations sociales exprimées sous forme de texte, d’image ou d’émoticône.

a) Explications détaillées de la solution.

Parmi 73 solutions, 31 (42,5 %) ne contenaient que la réponse, 17 (23,3 %) contenaient la réponse accompagnée d’une brève explication, souvent sous forme d’une courte phrase comme, par exemple « L’angle est obtus, car c’est un angle dont la mesure se situe entre 90 et 180 degrés ». Il n’y avait toutefois pas de détails quant à la façon dont la réponse a été obtenue. Citons également un autre élève qui a fait référence à son travail fait en papier - crayon : « l'angle que l'horloge d'écris est obtue je ne peu pas le d'écrire plus je lais faite sur un papier brouillon». Notons également que dans près d’un tiers (29,4 %) de solutions courtes, la réponse était accompagnée d’un dessin. Finalement, les 25 (34,3 %) d’autres solutions étaient plus élaborées.

En effet, cette disparité dans l’élaboration de la réponse illustre bien le caractère complexe de la tâche qui demande une mobilisation de plusieurs compétences d’ordre méthodologique, soit essayer, organiser sa démarche, mettre en œuvre une solution originale, en mesurer l'efficacité, argumenter à propos de sa solution ou de celle d'un autre, bref, les compétences peu travaillées par ailleurs, selon Charnay (Charnay, 1992). On peut également se rappeler de la recherche de Focant (Focant, 2003) qui a mis en évidence l’importance de favoriser les stratégies d’intervention garantissant une démarche de sélection et d’adaptation des procédures adéquates en fonction d’un répertoire de procédures interne à l’individu (autorégulation cognitive) jumelées avec le travail sur sa motivation, les facteurs indispensables pour que l’élève s’engage dans une résolution de problèmes mathématiques. Ces observations doivent cependant être cautionnées compte tenu la nature du contexte virtuel (à distance) ne nous permettant pas de rencontrer l’élève et lui poser des questions sur sa démarche. Le fait de ne pas présenter sa démarche complète ou le faire de façon partielle peut être dû au manque de temps, à l’accès au site limité.

b) Utilisation des outils de dessin

Les outils de dessin ont été utilisés par plusieurs élèves pour personnaliser leurs solutions. L’élève a soit utilisé l’image d’une horloge ou encore a fait son propre dessin de l’horloge. Il a ensuite indiqué les aiguilles et a déterminé la mesure de l’angle. Dans une solution, l’élève a indiqué qu’il s’est basé sur le dessin, mais au lieu de mettre le dessin, il a choisi d’expliquer ses étapes à l’aide de longues phrases textuelles : « Mon calcul est un peu dur à expliquer en mots, car mon travail est à base de dessins, mais je vais essayer quand même ». Du côté technologique, l’élève semble avoir utilisé un logiciel permettant de faire des dessins (MS Paint, par exemple) pour dessiner l’horloge et les aiguilles. Une fois enregistré sur le disque dur, le dessin pouvait être importé dans l’interface du site et ainsi inséré dans la solution (Figure 3). Finalement, l’élève pouvait juste mettre le lien vers l’emplacement de l’image. N’ayant pu capter le processus de rédaction, nous nous retrouvons ainsi devant un produit final, ce qui rend impossible à préciser la procédure choisie par l’élève, c’est-à-dire qu’il est impossible d’avoir plus de détail sur la rédaction de solutions. Nous pouvons quand même constater une grande variété de moyens de représentation comme démonstration d’une certaine créativité grâce aux options que l’environnement virtuel leur fournissait pour communiquer leurs démarches.

Figure 3 • Dessin inséré dans la solution

L’élève qui s’est servi du dessin comme représentation schématique des relations spatiales (5 lignes entre les deux chiffres) pour les associer aux relations entre les nombres et ainsi avancer dans son processus de résolution de problèmes contrairement à un autre élève qui s’est contenté de l’observation directe de ce qu’il voyait directement sur le dessin de l’horloge (Figure 2) pour produire immédiatement une réponse, sans passer par la formation de relations logico-mathématiques. Cette différence notée également par van Garderen et Montague (van Garderen et Montagne, 2003) distingue souvent un élève qui résout les problèmes avec succès comparé à l’autre qui peut présenter des difficultés d’apprentissage et nécessite donc un effort d’encadrement plus soutenu de la part de l’enseignant. L’analyse de deux cas fait ressortir le besoin d’un regard plus nuancé sur le rôle de représentations visuelles comme support à la résolution de problèmes avec plus de succès documenté, entre autres, par Güler et Çiltaş (Güler et Çiltaş, 2011).

c) Utilisation de formules et de symboles

La plupart des élèves semblent se contenter d’un raisonnement qualitatif exprimé à l’aide des phrases en langage de tous les jours sans recours au langage symbolique mathématique (formules, symboles d’opérations, etc.). Par contre, dans les 20 % des solutions où le calcul était présent, nous avons pu observer des raisonnements plus quantitatifs, voire algébriques. Dans une solution, l’élève a remarqué que l’angle était presque plat (estimation). Pour préciser sa mesure, il a donc effectué une soustraction en déterminant le nombre de degrés qui manquaient afin d’obtenir un angle plat et a soustrait son résultat de 180 degrés (calcul exact). Dans une autre solution, l’élève s’est servi de l’angle plein (360 degrés) et a déterminé la relation entre le nombre de traits sur la surface de l’horloge et l’angle plein. Par la suite, il a déterminé le nombre de lignes entre les deux aiguilles, ce qui lui a permis d’avoir une mesure plus précise de 174 degrés (raisonnement proportionnel, Figure 4). Dans les autres solutions, les élèves se sont basés sur le nombre d’heures et de minutes calculées à partir des positions des aiguilles formant l’angle, en se servant, au besoin, des rapports.

Figure 4 • Exemple du raisonnement proportionnel et du calcul

Comme le démontrent nos analyses, le recours à ce type de raisonnement plus abstrait est rare. Déjà, comme le relatent Neria et Amit (Neria et Amit, 2004), très peu d’élèves, qui sont souvent de bons élèves (‘high achievers’) choisissent de communiquer leurs solutions aux problèmes à l’aide des représentations algébriques, même après des années d’étude extensive d’algèbre, comme c’est le cas dans leur étude. Les auteurs expliquent le phénomène comme étant lié aux difficultés des élèves avec le caractère abstrait de l’algèbre, ainsi que la façon d’enseigner l’algèbre à l’école – un enjeu qui mérite d’être examiné par des personnes responsables des curricula, ainsi que par les enseignants (Neria et Amit, 2004).

d) Étapes de la résolution et réflexion sur sa démarche

Nous avons remarqué que 40 % des solutions détaillées étaient bien structurées, c’est-à-dire que les élèves prenaient le temps de bien identifier chacune des étapes de la solution : données, travail, réponse, question, etc. Ces élèves semblent ainsi avoir reproduit le modèle « uniforme » souvent enseigné dans les salles de classe. Un nombre assez important de solutions moins bien structurées rendant difficile l’évaluation de la qualité du raisonnement amène une problématique déjà bien documentée en recherche. Par exemple, Cai et al. (Cai et al., 1996) ont noté le besoin de bien articuler la démarche de résolution de problèmes pour qu’elle soit comprise par une autre personne. Cette observation est particulièrement pertinente dans le cas de la communication dans un espace virtuel car le retour (évaluation formative de la solution) est plutôt difficile lorsque le travail de l’élève est incomplet (Cai et al., 1996). Il serait ainsi important que les concepteurs du site trouvent des approches innovantes pour guider l’élève dans sa démarche de façon plus soutenue.

Très peu d’élèves communiquaient leurs réflexions de la démarche. Dans une solution, l’élève a indiqué qu’il a dû aller consulter son « journal de mathématiques afin de récupérer les informations nécessaires pour résoudre le problème ». Dans une solution, l’élève se faisait des rappels pour se guider dans son processus. Il a indiqué qu’il y avait « un angle de 6 degrés entre 2 lignes sur l’horloge ». De plus, il a indiqué qu’on « ne doit pas oublier que les aiguilles continuent toujours à avancer ». Nos observations mettent en évidence encore une fois le rôle de la métacognition pour soutenir l’apprentissage de mathématiques, une habileté qui mérite d’être explicitement enseignée au profit des élèves dites ‘réguliers’, ainsi que de leurs pairs dont les résultats sont inférieurs, comme le soulignent Schneider et Artelt (Schneider et Artelt, 2011). On se demande si le contexte de résolutions de problèmes dans un espace virtuel, tel que le site CASMI, ne pourrait fournir plus de support aux enseignants et aux élèves dans le développement de ces habiletés.

6. Conclusion

Afin de comprendre la valeur ajoutée de l’usage éducatif du site Internet CAMI (CASMI, selon les étapes de développement) dans les cours de mathématiques, nous avons examiné les données d’entrevues semi-dirigées avec les élèves francophones du Nouveau-Brunswick (Canada) et leurs enseignants. Les sept thèmes ressortis indiquent un niveau assez élevé d’appréciation de cette ressource virtuelle. En effet, le site semble être motivant pour les élèves et sert d’une bonne ressource éducative pour les enseignants. De plus, les élèves ainsi que les enseignants semblent apprécier les défis qui sont posés de façon hebdomadaire sur le site. Les élèves peuvent donc s’engager dans un processus de résolution de problèmes, en élaborant leurs propres démarches, et en les partageant avec les enseignants et leurs pairs. Selon les perceptions des élèves et de leurs enseignants, en plus d’augmenter leur confiance à l’égard des mathématiques, le site leur a permis d’améliorer leurs apprentissages en mathématiques tout en suivant leur style et leur rythme d’apprentissage, donc favorise une approche différenciée. Les élèves ont aussi mentionné qu’ils appréciaient les rétroactions qu’ils recevaient par rapport aux problèmes qu’ils résolvaient en les trouvant claires et expliquant bien leurs erreurs.

Cependant, l’impact réel de ces rétroactions est encore à vérifier d’autant plus que très peu d’élèves les consultent, selon nos statistiques (Freiman et Lirette-Pitre, 2009b). Nous pouvons même nous questionner sur une possibilité de faire un retour sur les productions des élèves à l’aide des outils d’interaction virtuelle existants tels que le forum de discussion ou d’autres pouvant favoriser un échange entre les élèves et les étudiants mentors de l’Université. Malgré la structure dynamique de la base de données CASMI, les activités pédagogiques sur le site semblent demeurer plutôt statiques, limitant les pratiques de résolution de problèmes à la production et le dépôt de solutions. Autre que les échanges en classe mentionnés par les enseignants, il ne semble pas y avoir beaucoup d’interactions entre les membres.

Pour ce qui est de la communication mathématique des solutions dans la communauté virtuelle CASMI, nous avons pu observer une grande variété de stratégies et de moyens de représentation dans les productions des élèves. Les élèves semblent vouloir personnaliser davantage leurs solutions en utilisant différentes polices, tailles de caractère, formats et couleurs en exprimant aussi des émotions en utilisant des émoticônes, ce que nous ne retrouvons pas généralement dans les solutions en format papier et crayon. Même si nous voyons ces aspects positifs dans les solutions, nous pouvons repérer plusieurs défis limitant l’impact du site sur les apprentissages des élèves.

Tout d’abord, nous avons remarqué que certains élèves sembleraient éprouver des difficultés au niveau du dessin étant donné qu’il n’y a pas d’outils spécifiques pour faire des dessins. Un dessin peut seulement être affiché comme une image. De plus, dans plusieurs solutions soumises à l’aide d’un formulaire électronique, nous voyons peu de traces de démarches mathématiques détaillées, car la plupart des élèves se limitent à des explications courtes, ou encore, mettent seulement des réponses finales. Il serait donc intéressant de rendre les options de création de fichiers audio et vidéo plus visibles et mieux accessibles dans la barre d’outils. La seule façon dont ceci peut être fait dans la version actuelle c’est en utilisant le lien hypertexte qui va diriger les élèves vers le contenu d’un fichier.

Par exemple, il serait intéressant que les élèves puissent cliquer sur un bouton et qu’une vidéo de la capture de son écran soit créée. De cette façon, il serait possible de pouvoir observer toutes les traces du travail de l’élève, ce qui pourrait aussi enrichir davantage les possibilités de réaliser des recherches plus poussées sur la nature des raisonnements des élèves engagés dans un processus de résolution de problèmes. Des outils mathématiques pourraient être implantés dans le formulaire de réponse, par exemple, une règle, un rapporteur d’angles, un compas, une fonction pour insérer des équations, etc. Ceci pourrait possiblement augmenter le niveau d’interactivité dans la manipulation des outils dans un environnement virtuel. De plus, peut-être qu’en ayant un formulaire permettant d’écrire des équations mathématiques de façon plus conviviale, les élèves auraient plus tendance à démontrer leurs calculs. Ces types de changements pourraient aider à mieux adapter le site aux besoins d’un plus grand nombre d’élèves incluant ceux ayant des difficultés en lecture et en écriture.

En reconnaissant une évolution constante des outils informatiques, dans une perspective de réseautage social web 2.0, dans nos réflexions sur l’avancement du projet, nous nous référons au concept de la Génération Net introduit dans les travaux de Prensky (Prensky, 2001) et Tapscott (Tapscott, 2009). À la lumière des résultats de nos analyses, nous nous interrogeons également sur d’autres approches, plus innovatrices, exploitant les nouvelles façons d’apprendre chez les jeunes. En naviguant librement dans les réseaux sociaux sur l’Internet, grâce à l’évolution rapide des ressources numériques disponibles, les apprenants de la Génération Net sont plutôt caractérisés comme étant autodidactes. En effet, ils n’ont pas besoin de manuels qui décrivent étape par étape comment exécuter une telle tâche, mais font plutôt référence à quelques brèves explications visuelles. Ces gens veulent les informations rapidement, sont capables de faire plusieurs tâches en même temps (multitasking). De plus, ces « net genners » ne tolèrent pas les longs discours et préfèrent consulter les informations en ligne à l’aide d’interactions sociales avec des gens de leur milieu ou encore avec des professionnels (Veen et Vrakking, 2006), ce qui ne semble pas être le cas dans la communauté CASMI.

Parmi les caractéristiques de la Génération Net mentionnées, entre autres, par Veen et Vrakking (Veen et Vrakking, 2006) et Gokhale, (Gokhale, 2007), on note l’intérêt des jeunes aux apprentissages plus actifs ainsi qu’aux activités de collaboration et de travail en groupe, peu exploité dans notre projet. Pour le moment, il existe très peu d’options de partages de solutions dans la communauté CASMI. Les élèves résolvent les problèmes et apportent leurs idées ingénieuses reflétant leurs conceptions mathématiques qui peuvent être alternatives ou même erronées, mais potentiellement riches en débats et en discussions. Par contre, ces solutions ne sont visibles qu’aux mentors qui les corrigent. Pourtant, le site offre une possibilité de création de micro-communauté donnant l’accès aux portfolios à d’autres membres. Pourquoi cette option est-elle sous-utilisée ? Nous jugeons ainsi qu’il devrait y avoir plus d’occasions de partage à l’intérieur du site.

Le forum de discussion serait une option possible. Par contre, peu de messages dans le forum démontrent que les élèves préfèrent mieux utiliser cet outil comme moyen de socialisation au lieu de moyen de discussions et de partages (Freiman et Lirette-Pitre, 2009b). Une étude doctorale portant sur le raisonnement algébrique chez les élèves du primaire dans un contexte d’utilisation d’un forum de discussion, réalisée par LeBlanc (Leblanc, 2011), semble encourager le passage des preuves pragmatiques aux preuves intellectuelles, en plus de favoriser une utilisation adéquate des règles du débat mathématique. Ainsi, un travail plus collaboratif en résolution de problèmes mathématiques avec les échanges en direct ou via les forums de discussion qui semble être prometteur (Stahl, 2006) ; (Freiman, 2009) peut-il transformer le site CASMI en véritable communauté de création et des échanges en temps « réel » ?

Pour conclure, nous voyons en la communauté virtuelle CASMI une ressource éducative émergente potentiellement riche pour favoriser les apprentissages des élèves en résolution de problèmes mathématiques. Mais, pour mieux explorer ce potentiel, il faudra effectuer des analyses plus poussées et diversifiées des relations complexes entourant l’usage didactique des technologies pour soutenir l’apprentissage de mathématiques. En revenant sur notre questionnement de départ sur les pratiques d’enseignement, nous partageons les réflexions d’Artigue (Artigue, 2011) sur les changements de paradigmes liés à l’utilisation des outils informatiques qui devraient s’appuyer sur une variété de théories pouvant éclairer la complexité de pratiques actuelles, la dynamique de leurs évolutions en les mettant en perspective de formation didactique initiale et continue des enseignants axée sur une meilleure réponse à leurs besoins et ceux de leurs élèves. Cette piste de recherche reste encore ouverte.

¹ Dans cet article, nous recourrons à la forme éponyme lorsqu’il est fait mention des genres, cela sans préjudice au genre réel des individus dont il sera fait état et simplement par souci d’économie stylistique ou éditoriale

BIBLIOGRAPHIE

ARSAC G., MANTE M. (2005). Les pratiques du problème ouvert. Lyon, édition Scéren.

ARTIGUE, M. (2011). L’impact curriculaire des technologies sur l’éducation mathématique. In A. Ruiz & E. Mancera (Eds.), Actas del CIAEM XIII Recife: Universidade Federale de Pernambuco.

BROUSSEAU, G. (1998). Théorie des situations didactiques. Grenoble : La pensée sauvage. 395 p. Coll. Recherches en didactique des mathématiques.

CAI, J., LANE, S., JAKABCSIN, M. S. (1996). The role of open-ended tasks and holistic scoring rubrics: Assessing students' mathematical reasoning and communication. In P. C. Elliott (Ed.), Communication in mathematics: K-12 and beyond (pp. 137-145). 1996 Yearbook of the National Council of Teachers of Mathematics. Reston, VA: NCTM.

CHAN, C. (2008). The use of mathematical modelling tasks to develop creativity. Dans E. Veikova, et A. Andzans, (dir.) Promoting creativity for all students in mathematics education. Rousse, Bulgaria: University of Rousse.

CHARNAY R. (1992-1993). Problème ouvert problème pour chercher, Grand N, n°51, p. 77 - 83.

CORBEIL N., PELLETIER M., PALLASCIO R. (2001). Les situations-problèmes : au coeur de la réforme en mathématiques, Instantanés mathématiques, printemps 2001, p. 14 - 27.

DE CORTé E., MASUI C. (2008). Enhancing the learning proficiency of students in higher education. Forum on Public Policy: A Journal of the Oxford Round Table.

DIEZMANN C., WATTERS J. (2004). Challenge and connectedness in the mathematics classroom; using lateral strategies with gifted elementary students. Paper presented at the 10th International Congress on Mathematical Education, July 4-11, Copenhagen, Denmark.

FOCANT J. (2003). Impact des capacités d'autorégulation en résolution de problèmes chez les enfants de 10 ans. Éducation et francophonie Vol. 31n°. 2.

FREIMAN V. (2009). Mathematical E-nrichment: Problem-of-the-week model. Dans R. Leikin, A. Berman, & B. Koichu (dir.): Creativity in Mathematics and the Education of Gifted Students, Rotterdam, Netherlands: Sense Publishing.

FREIMAN V. (2010). Complexité de la formation initiale des enseignants en mathématiques au primaire en milieu francophone minoritaire : le cas du Nouveau-Brunswick. Dans J. Proulx et L. Gattuson (dir.) Formation des enseignants en mathématiques : tendances et perspectives actuelles. Sherbrooke, Qc : Éditions du CRP p. 201-214.

FREIMAN V., APPLEBAUM M. (2011). Online Mathematical Competition: Using Virtual Marathon to Challenge Promising Students and to Develop Their Persistence. Canadian Journal of Science, Mathematics and Technology Education, Vol. 11, n°1, January 2011, p. 55 – 66.

FREIMAN V., LIRETTE-PITRE N. (2009a). Un regard didactique critique sur une communauté virtuelle d’apprentissages scientifiques et mathématiques interactifs. Dans F. Larose, A. Jaillet (dir.) : Le numérique dans l’enseignement et la formation. Analyses, traces et usages. Paris, France : L’Harmattan.

FREIMAN V. LIRETTE-PITRE N. (2009b). Building a virtual learning community of problem solvers: example of CASMI community. ZDM- The International Journal in Mathematics Education, Vol. 41 n° 1-2, p. 245-256.

FREIMAN V., MANUEL D., LIRETTE-PITRE N. (2007). CASMI Virtual Learning Collaborative Environment for Mathematical Enrichment. Understanding our Gifted, summer 2007, p. 20-23.

FREIMAN, V., VéZINA, N., GANDAHO, I. (2005). New Brunswick pre-service teachers communicate with schoolchildren about mathematical problems: CAMI project. ZDM-Zentralblatt fuer Didaktik der Mathematik, Vol. 37 n° 3, p. 178-190.

FREIMAN, V., VéZINA, N., LANGLAIS, M. (2005). Le Chantier d’Apprentissages Mathématiques Interactifs (CAMI) accompagne la réforme au Nouveau-Brunswick. Mathématique virtuelle à l’attention du primaire. Disponible sur Internet : http://spip.cslaval.qc.ca/mathvip/rubrique.php3?id_rubrique=18 (consulté le 31 janvier 2013).

FOURNIER H., BLAIN S., ESSIEMBRE C., FREIMAN V., LIRETTE-PITRE N., VILLENNEUVE D., CORMIER M., CLAVET P. (2006). Project ADOP: A Conceptual and Methodological Framework for Assessing the Effects of Direct Access to Notebook Computers. Dans E. Pearson et P. Bohman (dir.), Proceedings of World Conference on Educational Multimedia, Hypermedia and Telecommunications 2006. Chesapeake, VA: AACE.

GADANIDIS G. (2001). Web-based multimedia activities as pedagogical models. Proceedings of the Asian Technology Conference in Mathematics, RMIT University, Melbourne, Australia, p. 223-232.

GOKHALE A. A. (2007). Effectiveness of Online Learning Communities to Enhance Student Learning. Digitallearning Vol. 3 n° 7, p. 17-19.

GREENES C. (1997). Honing the abilities of the mathematically promising. Mathematics Teacher, Vol. 90 n°7, p. 582-586.

GROSJEAN S. (2007). Genèse d’une communauté virtuelle d’apprenants dans le cadre d’une démarche d’apprentissage collaboratif à distance. Revue Canadienne de l’Apprentissage et de la Technologie (RCAT) - Canadian Journal of Learning and Technology (CJLT), Vol. 33 n°1, p. 59-84.

GüLER G. ÇILTAş A. (2011). The visual representation usage levels of mathematics teachers and students in solving verbal problems, International Journal of Humanities and Social Science, Vol. 1 n° 11 p. 145-154

HANCOCK C. L. (1995). Implementing the assessment standards for school mathematics: Enhancing mathematics learning with open-ended questions. Mathematics Teacher, Vol. 88 n°6, p. 496-499.

HERSANT M. (2003). L’utilisation de bases de problèmes en classe de mathématiques. Un exemple avec “ La proportionnalité à travers des problèmes ”, Colloque international Intégration des technologies dans l’enseignement des mathématiques, Reims. Disponible en ligne :
http://www.reims.iufm.fr/Recherche/ereca/itemcom/.(consulté le 20 nov. 2013)

HOUDEMENT C. (2009). Une place pour les problèmes pour chercher. Annales de Didactique et de Sciences Cognitives n°14, p. 31-60.

JULO J. (1995). Représentation des problèmes et réussite en mathématiques – Un apport de la psychologie cognitive à l’enseignement. Presses Universitaires de Rennes.

KENNEWELL S. (2004). Meeting the standards in using ICT for secondary teaching: A Guide for ITT NC. New York, NY: RoutlegeFalmer.

KITCHNER K. S. (1983). Cognition, metacognition, and epistemic cognition : A three-level model of cognitive processing. Human Development, n°26, p. 222-232.

KLOTZ G. (2003). Math: Calculating the Benefits of Cybersessions. Dans D. T. Gordon (dir.) The Digital Classroom: how technology is changing the way we teach and learn. Cambridge, MA Harvard Education Letter.

KUNTZ G. (2007). Des mathématiques en ligne pour renouveler l’enseignement de mathématiques. Repères - IREM , n° 66, p. 104-113.

LEBLANC M. (2011). Étude de situations de validation en algèbre vécues par des élèves de 13 et 14 ans à l’aide et sans l’aide d’un forum électronique. Thèse doctorale. Université de Montréal.

LEBLANC M., FREIMAN V. (2011). Mathematical and Didactical Enrichment for Pre-service Teachers: Mentoring Online Problem Solving in the CASMI project. Montana Mathematics Enthusiast, Vol. 8 n° 1-2, p. 291-318.

LEIKIN R., LEVAV-WAYNBERG A., GUREVICH I, MEDNIKOV L. (2006). Implementation of multiple solution connecting tasks: Do students’ attitudes support teachers’ reluctance? Focus on Learning Problems in Mathematics, n° 28, p. 1-22.

MANN, E. (2005). Mathematical Creativity and School Mathematics: Indicators of Mathematical Creativity in Middle School Students. Unpublished Doctoral dissertation, University of Connecticut.

MANUEL D. (2010). Étude de la créativité mathématique dans les solutions problèmes proposés dans la communauté virtuelle CASMI. Thèse de maîtrise inédite, Université de Moncton. Moncton.

MANUEL D., FREIMAN V., BOURQUE J. (2012). Richesse des problèmes posés et créativité des solutions soumises dans la Communauté d'apprentissages scientifiques et mathématiques interactifs (CASMI). Éducation francophone en milieu minoritaire, Vol. 7 n°1, p. 1-18. Disponible sur internet :
http://www.reefmm.org/Notrerevue/v7n1manuelfreimanbourque_000.pdf, (consulté le 1 aout 2013).

Ministère de l’Éducation et du Développement de la Petite Enfance du Nouveau-Brunswick (2011). Programmes d'études : Mathématiques 30131. Fredericton : Ministère de l'Éducation ; Direction des services pédagogiques.

MINISTèRE DE L’ÉDUCATION DU NOUVEAU-BRUNSWICK (2005). Programme d’études. Mathématiques, 5e année. Fredericton, N.-B : Gouvernement du Nouveau-Brunswick.

MINISTèRE DE L’ÉDUCATION DU NOUVEAU-BRUNSWICK (2008). Cadre d’évaluation. Mathématiques, 5e année. Fredericton, N.-B : Gouvernement du Nouveau-Brunswick.

MINISTèRE DE L’ÉDUCATION DU QUEBEC (2001). Programme de formation de l’école québécoise. Québec, Qc: Gouvernement du Québec.

MURPHY E. (2004). Identifying and measuring ill-structured problem formulation and resolution in online asynchronous discussions. Canadian Journal of Learning and Technology, Vol. 30 n°1, p. 5-20.

NATIONAL COUNCIL OF TEACHERS OF MATHEMATICS (2000). Principals and Standards for School Mathematics. Reston, VA: NCTM.

NERIA D., AMIT M. (2004). Students preference of non-Algebraic representations in mathematical communication. International Group for the Psychology of Mathematics Education, n°3, 409-416.

ORGANISATION FOR ECONOMIC CO-OPERATION AND DEVELOPMENT. Measuring Student Knowledge and Skills : A New Framework for Assessment. OECD, Disponible sur Internet :
http://www.pisa.oecd.org/dataoecd/45/32/33693997.pdf (consulté le 31 janvier, 2013).

PALLASCIO R. (2003). L'Agora de Pythagore : une communauté virtuelle philosophique sur les mathématiques. Dans A. Taurisson (dir.) Pédagogie.net : l’essor de communautés virtuelles d’apprentissage. Québec: Presses de l’Université du Québec.

PALLASCIO R. (2005). Les situations-problèmes : Un concept central du nouveau programme de mathématique. Vie pédagogique, Vol. 136, p. 32-35.

PELCZER I., FREIMAN V. (2009). Problem solving and institualization of knowledge. Dans : CIEAEM-61. Pré-actes/Pre-proceedings, Montréal, Qc : Université de Montréal.

PIGGOTT J. (2007). The nature of mathematical enrichment: a case study of Implementation. Educate Vol. 7 n° 2, p. 30-45.

PIMTA S., TAYRUAKHAM S., NUANGCHALERM P. (2009). Factors Influencing Mathematic Problem-Solving Ability of Sixth Grade Students, Journal of Social Sciences, Vol. 5 n°4, p. 381-385.

POIRIER L. (2001). Enseigner les maths au primaire : Notes didactiques. St.-Laurent, Qc.: Éditions du renouveau pédagogique.

PRENSKY M. (2001). Digital natives, digital immigrants. On the Horizon, Vol. 5, p. 1-6.

RABARDEL P. (1995) Qu’est-ce qu’un instrument ? Appropriation, conceptualisation, mises en situation. Les dossiers de l’ingénierie éducative, Vol. 19, p. 61-65. CNDP.

RENNINGER K. A., SHUMAR W. (2002). Building Virtual Communities: Learning and Change in Cyberspace. New York, NY: Cambridge University Press.

SABRA H., TROUCHE L. (2009). Enseignement des mathématiques et TICE, Revue de la littérature de recherche francophone (2002 – 2008), Lyon, France: INRP.

SOKHNA M., DIA E. M. (2009). Approche instrumentale de Ressources pédagogiques pour la formation des professeurs de mathématiques. Ecritures plurielles, revue semestrielle d’études universitaires, n° 03.

SCHLEICHER A. (1999). Measuring Student Knowledge and Skills: A New Framework for Assessment. Paris : Organization for Economic Co-operation and Development.

SCHNEIDER W., ARTELT C. (2010). Metacognition and mathematics education. ZDM – International Journal of Mathematics Education, Vol. 42, n°2, p. 149-161

STAHL G. (2006). Group Cognition: Computer Support for Building Collaborative Knowledge. Cambridge, MA: MIT Press.

TAURISSON A. (2003). Réflexion générale : Le sens, l’ingénierie et la mise en place des communautés virtuelles d’apprentissage. Dans A. Taurisson (dir.) Pédagogie.net : l’essor de communautés virtuelles d’apprentissage. Québec: Presses de l’Université du Québec.

TAKAHASHI A. (2000). Open-ended Problem Solving Enriched by the Internet. NCTM annual meeting. Disponible sur Internet :
http://www.mste.uiuc.edu/users/aki/open_ended/ (consulté le 20 novembre 2013).

TAPSCOTT D. (2009). Grown up digital: how the net generation is changing your world. New York: McGraw-Hill.

THE MATH FORUM'S BRIDGING RESEARCH AND PRACTICE GROUP (2000). Encouraging mathematical thinking: Discourse around a rich problem. Disponible sur Internet: http://mathforum.org/brap/wrap/ (consulté le 31 janvier 2013).

VAN GARDEREN D., MONTAGUE M. (2003). Visual-spatial representation, mathematical problem solving and students of varying abilities. Learning Disabilities Research and Practice, Vol. 18 n°4, p. 246-254.

VEEN W., VRAKKING B. (2006). Homo Zappiens, Growing up in a Digital Age. London, UK: Network Continuum Education.

VéZINA, N., LANGLAIS, M. (2002). Résolution de problèmes, communication mathématique et TIC : l'expérience du projet CAMI. Nouvelles de l'AEFNB, Vol. 33 n° 5, p. 9-12.

WENGER E. (1998). Communities of Practice: Learning, Meaning, and Identity. Cambridge: Cambridge University Press.

ZODIK I., ZASLAVSKY O. (2004). Characteristics of Mathematical Problem Solving Tutoring in an Informal Setting. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education. PME.

A propos des auteurs

Viktor FREIMAN est professeur titulaire  à la Faculté des sciences de l’éducation de l’Université de Moncton depuis 2003. Ses recherches portent sur la didactique des mathématiques, l’intégration des TIC et la douance mathématiques. Il codirige une série des livres chez Springer Mathematics Education in the Digital Era (depuis 2011). Il était coresponsable du Forum canadien sur l’enseignement de mathématiques en 2009. Il a développé le Marathon virtuel des mathématiques (2010-2012). Il est président de l’Association APTICA (Avancement pédagogique des TIC en Atlantique.

Adresse : Faculté des sciences de l’éducation, Université de Moncton, Campus Moncton, Moncton, N.-B., Canada , E1A 3E9

Courriel : viktor.freiman@umoncton.ca

Dominic Manuel est présentement doctorant en éducation à l’Université McGill. Il s’intéresse particulièrement au développement du talent et de la créativité chez les élèves par l’entremise de tâches riches en mathématiques. Il est aussi chargé de cours en didactique des mathématiques au primaire et au secondaire. Il a enseigné à l’Université de Moncton de 2006 à 2012 et à l’Université McGill depuis 2012.

Adresse : Département d’études intégrées en éducation, Faculté d’éducation, Université McGill, 3700, rue McTavish, local 244, Montréal, QC, Canada, H3A 1Y2

Courriel : Dominic.manuel@mcgill.ca

Référence de l'article :

Viktor FREIMAN, Dominic MANUEL, Une ressource virtuelle de résolution de problèmes mathématiques : les perceptions d’utilisateurs et les traces d’usage, Revue STICEF, Volume 20, 2013, ISSN : 1764-7223, mis en ligne le 12/05/2014, http://sticef.org