Sciences et Technologies
Sciences et Technologiesde l´Information et
de la Communication pour
l´Éducation et la Formation
version à télécharger (pdf)
Volume 19, 2012
Article de recherche
|
Contact : infos@sticef.org |
Prise en compte des contradictions intra-apprenant dans le
diagnostic
|
|
|
|
|
|
|
1. Introduction
La personnalisation (terme utilisé au sein de la communauté EIAH) ou l’adaptation (terme utilisé au sein de la communauté IHM) ne vont pas de soi. En effet, « la personnalisation des EIAH est l’un des principaux verrous de leur développement [...] qui implique des modèles issus de l'informatique (apprentissage automatique, IHM, modélisation des connaissances et du raisonnement), des sciences de l'apprentissage (psychologie, didactique, pédagogie et sciences de l'éducation), de l'ergonomie, des sciences du langage et de la communication, et des mathématiques (statistique, logique). » (Cluster-ISLE, 2009).
La trace de l’activité de l’apprenant devient un facteur essentiel de la personnalisation puisque « la résolution du problème de la personnalisation des EIAH est essentiellement dépendante de la capacité à produire des traces pertinentes et exploitables de l'activité individuelle ou collective de l'apprenant qui interagit avec un EIAH » (Lund et Mille, 2009). Ainsi émergent des courants de recherche s’intéressant à la personnalisation de l’EIAH (Laroussi et Caron, 2010) par le tuteur et/ou par l’EIAH lui-même. Parmi les axes de recherche liés à l’exploitation des traces à une fin de personnalisation, nous pouvons identifier plusieurs démarches. Certaines se centrant sur l’adaptation des IHM elles-mêmes (Heili et Ollagnier-Beldame, 2008), (Vézian, 2008) alors que d’autres s’intéressent à la personnalisation à apporter à l’apprenant (Bouzeghoub et Kostadinov, 2005), (Sehaba et al., 2009), de la remédiation à apporter — tels le renvoi vers une fiche de cours, la proposition d’un nouveau problème à résoudre — (Jonassen et Grabowski, 1993), ou de la prise de décision pour le calcul de la rétroaction (Mayo et Mitrovic, 2001), (Mufti-Alchawafa, 2008). Ces dernières recherches se basent sur le calcul d’un diagnostic de l’activité de l’apprenant.
Aussi, et tel qu’indiqué par (Hibou et Py, 2006, p. 97) « c’est avec l’émergence des tuteurs intelligents qu’est apparue la nécessité de représenter les connaissances de l’apprenant au sein d’un " modèle de l’élève ", pour rendre les actions tutorielles plus efficaces ». Ces mêmes auteurs signalent que la conception d’un modèle de l’élève soulève deux problèmes : « d’une part le choix des caractéristiques individuelles (cognitives, comportementales) et de leur mode de représentation informatique dans l’EIAH ; d’autre part la mise en place de mécanismes de mise à jour de ce modèle à partir des évènements logiciels (ou "observables") recueillis durant l’interaction » (ibid. p. 98). Le processus d’inférence des caractéristiques individuelles (« hidden cognitive state », « the student’s Knowledge of the matter ») est appelé diagnostic cognitif, tel qu’introduit par (Van Lehn , 1988).
C’est dans ce cadre de recherche que nous nous plaçons, puisque grâce à la mise en exergue de ce que l’apprenant sait, ce qu’il sait faire et, aussi et surtout, ce sur quoi il éprouve des difficultés la personnalisation prend tout son sens. Établir un diagnostic permet de prendre des décisions adaptées à la situation diagnostiquée (Rasmussen, 1986), (Hoc et Amalberti, 1992). Cette prise de décision est d’autant plus complexe à mettre en œuvre lorsque le système détecte des situations de contradictions dans les propos, actes ou comportements d’un même apprenant.
Dans la suite de cet article, nous parlerons de contradiction intra-apprenant (CIA) pour désigner de telles situations. La représentation de ces CIA et leur traitement sont une des particularités de notre modèle de l’élève et de notre système de diagnostic.
Par ailleurs, nous nous intéressons à des environnements ouverts (dans le sens où plusieurs éléments du système sont indépendants et où il est donc difficile de prédire de façon exhaustive les actions d’un apprenant) et proposant à l’apprenant plusieurs modalités de résolution de problème (MRP) où une MRP est un outil informatique fourni à l’apprenant pour qu’il réalise une activité d’apprentissage. De tels environnements laissent la possibilité d’exprimer un nombre plus important de CIA qu’un environnement fermé de type tuteur intelligent classique qui contrôle la non-contradiction, tel que nous le verrons dans l’état de l’art. Le traitement des CIA nécessite, d’une part leur identification à partir de la combinaison, par le diagnostic, des traces issues des différents MRP, qui sont des outils indépendants. D’autre part, il est nécessaire, une fois des CIA identifiées, de décider de la façon dont elles sont prises en compte dans le modèle de l’élève. Dans ce travail nous explorons la prise en compte du contexte pour le traitement des CIA, c’est-à-dire la possibilité pour le système de diagnostic d’adapter la prise en compte des CIA en fonction des MRP impliquées.
Dans un premier temps nous positionnons notre travail vis-à-vis de l’état de l’art, en particulier la prise en compte des contextes dans les systèmes de diagnostics, les systèmes de diagnostics associés à des environnements ouverts, le rôle de la trace dans le calcul du diagnostic et enfin la prise en compte de l’incertitude dans ce type d’environnement.
Dans un second temps, nous exposons le modèle de diagnostic DiagElec en présentant les hypothèses sur lesquelles il est fondé ainsi que les méthodologies mises en œuvre, que ce soit lors de sa modélisation ou de son évaluation. Puis, nous présentons le diagnostic tel qu’il est établi au sein de DiagElec et, en particulier, la prise en compte des MRP et du contexte au sein de ses algorithmes, mais aussi la mise en évidence de contradictions intra-apprenant.
Afin d’évaluer notre modèle, nous exposons les expérimentations réalisées, ainsi que les études relatives à la prise en compte du contexte, des CIA et de leurs impacts sur les poids des MRP.
2. Etat de l’art
2.1. Prise en compte du contexte dans le système de diagnostic
(Jameson, 2003) et (Simonin et Carbonell, 2007) distinguent deux types d’adaptation selon le but et la finalité poursuivis, à savoir l’adaptation à l’environnement dans lequel se situe l’interaction et l’adaptation au profil de l’apprenant (appelée aussi personnalisation de l’interface), cette dernière pouvant s’effectuer de deux manières distinctes (Simonin et Carbonell, 2007) :
- Si l’apprenant peut adapter l’interaction à ses préférences personnelles, l’interface sera dite adaptable.
- Si l’interface est capable d’adapter, au cours de l’interaction, son comportement aux attentes, besoins et capacités de l’apprenant, l’interface sera dite adaptative.
Notre recherche se place dans le cadre de l’adaptation au profil de l’apprenant et plus précisément dans des situations d’interfaces adaptatives. Nous nous intéressons à des situations d’apprentissage dans lesquelles l’apprenant dispose de plusieurs modalités d’interaction pour résoudre un problème.
Des environnements informatiques intégrant un module de diagnostic et proposant plusieurs MRP pour une même activité d’apprentissage existent déjà. Nous pouvons citer par exemple Cabri-Euclide (Luengo, 2005) et Baghera (1) (Webber et al., 2001) dans le domaine de la géométrie ou Andes (2) en physique (VanLehn et al., 2005). Dans le cas d’Andes, l’apprenant est amené à résoudre des problèmes en utilisant plusieurs MRP comme l’écriture d’équations, le traçage de vecteurs (Figure 1(a)). Le diagnostic s’effectue en ne considérant que les équations écrites et une rétroaction sur ces équations est immédiatement donné à l’apprenant par le biais de couleurs (vert/rouge).

Figure 1. Environnements proposant plusieurs contextes de résolution
Dans le cas de la formulation de preuves en géométrie, les environnements Cabri-Euclide et Baghera (Figure 1(b) et (c)), permettent à l’apprenant de faire sa preuve à l’aide de deux modalités : le dessin et texte. Dans le cas de Cabri-Euclide, un agent vérifie à chaque instant la cohérence entre le dessin réalisé par l’apprenant et le texte formulé par celui-ci. L’environnement indique les incohérences à l’apprenant, qui doit corriger celles-ci pour que sa preuve soit validée. Dans le cas de Baghera, le système ne vérifie pas si les énoncés proposés correspondent à la figure ainsi le diagnostic ne considère que la production textuelle.
De tels environnements sont plus riches que des environnements ne proposant qu’une seule modalité, de par la complétude des modalités proposées à l’apprenant qui travaille ainsi sur différentes MRP. Néanmoins ils ne prennent pas en compte cette richesse dans leur diagnostic.
Notre travail est guidé par l’idée que prendre en compte les productions de l’apprenant, exprimées dans plusieurs MRP, permet d’avoir une représentation plus fine des connaissances de l’élève. Cette représentation permettra la production d’un diagnostic fin de l’activité de l’apprenant, qui sera le support à une rétroaction mieux adaptée et personnalisée à fournir à l’apprenant.
Ce point de vue rejoint celui de (Vassileva et al., 2002) qui indique que la capacité à interpréter des informations provenant de sources hétérogènes et de les intégrer à un modèle de l’apprenant permet de créer du sens. La prise en compte de données issues de sources hétérogènes (dans notre cas les MRP, le contexte du problème lui-même) se retrouve dans des problématiques de personnalisation de la rétroaction ou des aides à fournir à l’apprenant. Par exemple, si nous reprenons le cas de l’environnement Andes, le système propose à l’apprenant des aides plus ou moins fines (allant du conseil « succinct » à la démarche à suivre) afin que celui-ci corrige ses erreurs. Comme ces erreurs peuvent apparaître dans différentes MRP, le système adapte son retour en fonction des informations recueillies mais aussi, et surtout, de la provenance de ces informations, autrement dit les MRP. Dans ce dernier exemple, le diagnostic considère séparément chaque MPR, dans notre démarche nous cherchons à produire le diagnostic en associant plusieurs MRP.
Du point de vue des modèles de diagnostic, deux grandes approches émergent dans les tuteurs intelligents (Goguadze et Melis, 2009) :
– L’approche générative fortement représentée par la méthode de diagnostic dite par traçage de modèle (ou model tracing en anglais), (Corbett et Anderson, 1995). Ici, les pas de résolution (identifiés comme erronés ou non) d’un problème sont générés de la façon la plus exhaustive possible. À chaque étape de résolution de l’élève, le diagnostic vise à estimer si la connaissance associée à cette étape est apprise ou non, en comparant la réponse de l’élève à l’un des pas de résolution anticipés.
– L’approche évaluative représentée par la méthode dite orientée contraintes (ou Constraint-Based Modeling en anglais), (Ohlsson, 1992) où les erreurs sont décrites sous forme de contraintes. Si aucune contrainte n’est enfreinte, alors la réponse est supposée correcte. Une erreur est donc une contrainte qui a été enfreinte. Le diagnostic sur une connaissance analyse le rapport entre les erreurs et les connaissances associées aux problèmes. C'est-à-dire les règles enfreintes vs les règles non enfreintes.
Néanmoins, ces deux approches n’abordent pas la notion du contexte. En effet, elles sont élaborées vis-à-vis d’un ensemble de problèmes et d’un domaine de connaissances, mais sans prendre en compte des ressources et des MRP pouvant intervenir.
Dans notre environnement, nous disposons d’une représentation du contexte du problème à l’aide de méta-données, ce qui rejoint le point de vue d’autres auteurs (Butoianu et al., 2010). Lors de la résolution du problème par un apprenant, toutes les données relatives à celui-ci sont considérées dans le calcul du diagnostic.
2.2. La prise en compte des contradictions dans des systèmes de diagnostics intégrés à des environnements ouverts
Les systèmes de diagnostic informatiques dans les EIAH sont classiquement intégrés au sein d’environnements que nous qualifions de fermés et contrôlés.
– L’environnement est fermé dans le sens où toutes les MRP proposées à l’apprenant ont été développées pour l’environnement et où il est difficile d’intégrer une MRP conçue par ailleurs.
– L’environnement est contrôlé dans le sens où les actions de l’apprenant sont décrites de façon exhaustive (comme dans l’approche générative décrite précédemment) et le système ne laisse pas l’apprenant s’éloigner de cette description.
Nous pourrons citer à titre d’exemples les environnements Assistement (Razzaq et al., 2008), et SimQuest (Van Joolingen et De Jong, 2003), qui est représenté Figure 2.

Figure 2. SimQuest : Un exemple d’environnement fermé et contrôlé
Or depuis quelques années, les apprenants travaillent de plus en plus avec des environnements que nous qualifions d’ouverts car ils associent plusieurs ressources indépendantes. Dans ces environnements, les actions et le comportement de l’apprenant peuvent être difficilement contrôlés de façon exhaustive. La plupart de ces environnements ouverts proposent à l’apprenant des activités de différentes natures, qui peuvent être conduites et résolues selon différentes MRP. C’est le cas des laboratoires virtuels ou des nouvelles plateformes pédagogiques proposant des activités d’investigation, et où plusieurs MRP sont combinées au sein d’une activité pédagogique. Par exemple, dans le cas de la plateforme SCY – Science Created by You – (d’Ham et al., 2009), le système informatique fournit à l’apprenant des ressources indépendantes telles que des simulations, un éditeur de texte et de graphique afin qu’il puisse mener à bien la tâche demandée. Un autre exemple utilisé dans plusieurs domaines des sciences et véritablement utilisé dans les classes est la plateforme WISE (http://wise.berkeley.edu/).
Mais là encore, en dépit de la disponibilité de ces systèmes et/ou des recherches s’y rapportant, la majorité d’entre eux n’intègrent pas de diagnostic automatique. Une des raisons possibles est la nécessité de contrôle imposé par les modèles de diagnostic couramment développés. Ainsi, un exemple de plateforme ouverte qui intègre un système de diagnostic est la plateforme Active Math (Goguadze et Melis, 2009). Cependant le système de diagnostic n’associe pas plusieurs MRP et ne cherche pas des contradictions intra-apprenant.
Dans des environnements ouverts et proposant plusieurs MRP, la considération de ces dernières dans le diagnostic trouve sa justification et son intérêt lors de l’existence de contradictions intra-apprenant. Dans des expérimentations antérieures où l’apprenant pouvait s’exprimer à la fois par des réponses textuelles et répondre à des questionnaires à choix multiples (QCM), nous avons mis en évidence de telles contradictions (Michelet et al., 2007). Nous présentons une illustration de telles contradictions, issues de nos expérimentations, dans la Figure 3.
Si nous considérons uniquement les réponses de l’apprenant concernant le QCM, celles-ci sont correctes : l’appareil de mesure permettant de mesurer une intensité est bien un ampèremètre et celui-ci se place en série dans un circuit électrique. Ainsi, une analyse didactique des réponses aboutit au fait que l’apprenant sait le nom de l’appareil de mesure permettant de mesurer une intensité ainsi que son mode de branchement. Cependant, en regardant le circuit construit par l’apprenant afin de mesurer des intensités, nous constatons qu’il a placé des voltmètres dans le circuit au lieu de placer des ampèremètres, traduisant qu’il ne sait pas quel est l’appareil de mesure permettant de relever des intensités. Ce constat est confirmé par l’affichage des valeurs des appareils de mesure : si l’élève ne les avait pas calibrés, ils n’afficheraient pas de valeur et donc nous pourrions croire à une confusion dans les appareils de mesure due à l’interface de TPElec. Or les voltmètres affichent tous des valeurs de tension, et l’apprenant n’a pas modifié son circuit pour autant.
Ainsi, dans des situations de contradiction intra-apprenant, le diagnostic doit d’une part mettre en évidence la contradiction, et d’autre part, décider comment traiter cette contradiction. Dans notre cas la piste que nous avons mise en place est de traiter la contradiction en pondérant chaque MRP selon le contexte (étape du problème, type de connaissance, etc.).
MRP |
Question posée |
Réponse de l’apprenant |
QCM |
Quel est l’appareil de mesure permettant de mesurer une intensité et comment cet appareil se branche-t-il. |
|
TPElec |
Nous demandons à l’apprenant de placer des appareils de mesure dans un circuit, afin d’y relever l’intensité traversant chacune des lampes. |
|
Figure 3. Exemple de contradiction intra-apprenant
2.3. Place et rôle de la trace dans le diagnostic
« Dans un environnement ouvert qui offre à l’élève un large éventail de moyens d’expression de sa recherche et de sa résolution, le premier et principal problème est de déterminer avec suffisamment de précision ce que l’élève a fait, c’est-à-dire de trouver une première interprétation à des actions élémentaires elles-mêmes peu significatives. » (Blondel et al., 1997).
Cette phrase résume en elle-même la complexité d’établir du diagnostic dans des environnements ouverts proposant plusieurs MRP indépendantes. Puisque chaque MRP peut être indépendante, pour rendre compte de l’activité de l’apprenant dans chacune des MRP et analyser cette activité dans une finalité de diagnostic, une des solutions consiste à utiliser les traces provenant de chaque MRP, puis à les combiner afin d’identifier les connaissances mobilisées par l’apprenant lors de la résolution d’un problème ou le déroulement d’une activité.
Ici il convient de reprendre la distinction classique entre diagnostic comportemental et épistémique (Wenger, 1987), (Balacheff, 1994), (Hibou et Py, 2006). Le premier s’intéresse aux comportements et le deuxième à l’état de connaissances de l’apprenant. « Le diagnostic au niveau comportemental peut consister en une simple évaluation des entrées recueillies, sans inférence, ou bien inclure une étape de reconstruction des comportements non observés » (Hibou et Py, 2006 p. 103). Le diagnostic épistémique infère les connaissances de l’apprenant à partir des comportements ou des résultats du diagnostic comportemental.
Ainsi, pour pouvoir identifier des CIA nous effectuons un premier diagnostic comportemental qui prend en compte des traces d’activité venant de plusieurs MRP et qui reconstruit des comportements de type contradiction intra-apprenant, comportements qui ne sont pas observés directement dans les traces initiales. Les traces enrichies décrivant les contradictions sont donc le résultat de ce processus. À ce niveau le diagnostic est comportemental parce qu’il identifie, au sein d’une même situation d’apprentissage, des réponses correctes et incorrectes en rapport avec une même connaissance ou compétence.
2.4. Le diagnostic, une activité de nature incertaine
Le diagnostic cognitif et plus particulièrement le diagnostic épistémique, qui fait référence à l’état de connaissances de l’élève, est de nature empirique. En effet, un apprenant peut avoir une réponse correcte sans pour autant maitriser les connaissances qui lui sont associées et vice-versa.
De nombreux travaux, dès le début des tuteurs intelligents ont traité ce problème par des modèles théoriques de croyances (Gilmore et Self, 1988) et des raisonnements de type logique floue ou de croyance (Derry et al., 1989). Enfin, plus récemment des techniques numériques, tels que les réseaux bayésiens, sont largement utilisées dans les systèmes de diagnostic. Dans ces différents travaux l’objectif est de pouvoir représenter et/ou inférer le niveau de croyance (ou d’incertitude) du système par rapport à l’état des connaissances du sujet.
En ce qui nous concerne, le fait de détecter des CIA, dans une première étape du diagnostic est une information supplémentaire pour le système de croyances. En effet, l’identification d’une contradiction augmente l’incertitude à propos de la maîtrise d’une ou plusieurs connaissances. De plus, nous cherchons à identifier les facteurs liés au contexte de diagnostic qui interviennent dans la gestion du degré d’incertitude. Ainsi, quelques questions se posent : si dans une première étape de diagnostic, une CIA entre deux MRP est détectée, ces deux MRP doivent-elles être considérées de la même façon ? Cela dépend-il du type de problème ou de l’élément qui doit être diagnostiqué (une connaissance, une erreur ou une compétence) ? Pour répondre à ces questions nous avons conçu un modèle d’apprenant capable d’identifier des CIA et de prendre en compte différents contextes de natures différentes : le contexte d’interaction et le contexte de résolution. Ces propositions sont analysées vis-à-vis des expérimentations que nous avons mises en place.
3. Hypothèses et méthodologie
3.1. Hypothèses de recherche
Un des postulats de notre recherche est que la prise en compte des CIA dans le diagnostic permettra une meilleure adaptation et personnalisation lors de la production des rétroactions. Notre objectif ici est donc l’identification et le traitement des CIA dans le système de diagnostic.
Ainsi, nous étudions l’hypothèse de recherche suivante : la prise en compte de toutes les MRP permet au diagnostic de mettre en évidence des contradictions intra-apprenant et la considération du contexte de diagnostic permet d’affiner un traitement de ces CIA.
Nous introduisons le concept de contexte de diagnostic que nous définissons comme l’ensemble des traces collectées provenant de la combinaison des MRP, autrement dit, les traces collectées et enrichies issues d’un ou plusieurs outils informatiques.
Par ailleurs le traitement de ce contexte doit être dynamique puisqu’il dépend de la situation d’apprentissage en cours. Dans cet article, nous étudions le comportement du système en cas de contractions intra-apprenant, que ce soit à travers la même MRP ou entre plusieurs MRP. Les contradictions pouvant intervenir entre MRP, quel est l’impact de la MRP ? Ont-elles le même poids ?
Pour ce faire, nous avons fait des choix sur la manière de considérer les MRP, le contexte du problème, du scénario et nous souhaitons évaluer ces choix et leur impact. Dans ce but, nous travaillons selon deux axes : l’un informatique et l’autre didactique, puisque nous intégrons dans notre modélisation informatique des résultats provenant de ce dernier axe.
3.2. Démarches de recherche
3.2.1. Relative à la conception du modèle de diagnostic
Les hypothèses sur lesquelles repose notre système de diagnostic sont le fruit d’expérimentations antérieures (dites exploratoires) à sa modélisation (Michelet, 2005). L’analyse des productions d’apprenants collectées lors de celles-ci (Michelet et al., 2006) ont fait émerger des éléments à prendre en compte dans la conception du système de diagnostic tel l’apparition de contradictions intra-apprenants ainsi que de nombreuses occurrences de résolution d’un même problème pour un même apprenant.
Nous nous sommes basés sur ces observations pour la modélisation puis l’implémentation de notre système de diagnostic. Ensuite nous avons mené des expérimentations post-conception afin d’évaluer DiagElec, notre modèle. Ainsi, la méthodologie de la modélisation à l’évaluation de notre modèle suit les étapes suivantes : (1) Expérimentations exploratoires, (2) Modélisation et implémentation et (3) Expérimentations post-conception.
3.2.2. Relative à l’évaluation du modèle de diagnostic
Afin d’évaluer notre système de diagnostic, nous avons comparé les diagnostics issus de DiagElec à ceux produits par des enseignants. Afin de distinguer l’expertise humaine du système informatique, nous utilisons dans la suite l’expression ”experts humains” pour désigner ces enseignants. Dans leur article concernant la classification des méthodes d’évaluation des ITS, les auteurs (Iqbal et al., 1999) indiquent que « Comparison studies are a general class of methods which note similarities and differences between the behaviour or design of an ITS with a standard or even another system. » (ibid., p. 175).
Dans notre cas, nous mesurons la pertinence des diagnostics produits par la machine par comparaison avec ceux des experts humains, ce qui est un gold-standard en la matière (Hausmann et al., 2008).
4. L’environnement de résolution de problèmes
4.1. La démarche scientifique expérimentale
Dans l’activité de résolution de problèmes que nous proposons à l’apprenant, les problèmes sont tous basés sur le modèle de la démarche scientifique expérimentale (Giordan, 1999). Cette démarche (cf. Figure 4), définie comme un outil d’investigation (Calmettes, 2009) pour décrire et comprendre le réel, repose sur le questionnement et s’articule autour de l’expérimentation, dont l’impact sur la déstabilisation des éléments détectés est reconnu (Giordan, 1999), (de Vecchi, 2006).
Nous avons choisi cette démarche car elle :
– Est classiquement utilisée en classe de Sciences-Physiques (Viennot, 1996). Ainsi, nous plaçons les apprenants dans un contexte de démarche similaire à celui dont ils ont l’habitude en classe traditionnelle (Astolfi et al., 1997). De plus, l’électricité permet de déployer une démarche scientifique expérimentale dans sa globalité
– Permet de tester les savoirs, savoir-faire et erreurs de l’apprenant,
– Permet la mise en œuvre de différentes MRP, comme nous le développons dans le paragraphe suivant.
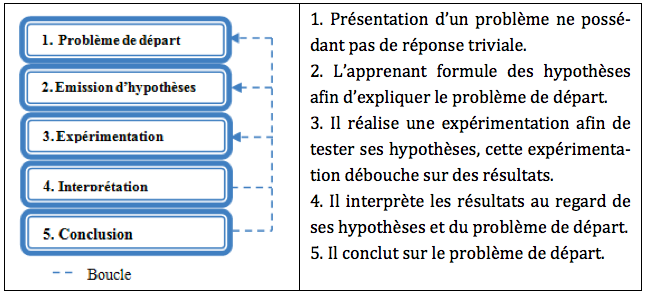
Figure 4 • Démarche scientifique expérimentale : les étapes
4.2. Personnalisation des situations proposées à l’apprenant
Plusieurs moyens d’expression peuvent être mis en œuvre afin de réaliser les étapes décrites à la Figure 5. Par exemple, l’étape 3 peut conduire à des activités pratiques menées sur ordinateur alors que l’étape 2 requiert une formulation (textuelle ou orale) de l’apprenant. De ce fait, nous proposons des situations de construction et de manipulation et des situations de formulation ; situations réalisables au moyen de différents outils informatiques.
4.2.1. Situation de construction et manipulation
Dans notre environnement, les situations de construction sont réalisables au moyen du micromonde TPElec (cf. Figure 5(a)). Le micromonde est un environnement informatique ouvert constitué « d’objets et de relations ; d’un ensemble d’opérateurs susceptibles d’opérer sur ces objets en en créant de nouveaux présentant certaines nouvelles relations et permettant un rapport plus ou moins clair avec le concept de manipulation directe » (Laborde, 1995). TPElec permet à un apprenant de construire des circuits électriques à partir de composants puis de les manipuler, comme par exemple d’agir sur des interrupteurs, de modifier les caractéristiques de composants, de changer des composants, d’en détruire, de modifier des branchements, etc. TPElec est développé sous forme d’application web pouvant s’intégrer dans les plateformes d’apprentissage.
4.2.2. Situation de formulation
Nous considérons comme Formulation de l’apprenant l’ensemble des productions en langage naturel de celui-ci, quelle que soit la nature syntaxique de celle-ci, et ce en direction de l’EIAH. Par exemple, l’argumentation, l’écriture d’un énoncé de loi sont des instances de formulations de l’apprenant. Les situations de formulation sont réalisables au moyen de formulaires (cf. Figure 5(b)).

Figure 5. Présentation des MRP Micromonde et Formulation en contexte
5. DiagElec, un diagnostic traitant les CIA
La façon dont nous avons développé le système de diagnostic est décrite de façon détaillée dans (Michelet, 2010), (Michelet et al., 2012a). Dans cet article nous développerons uniquement les aspects liés au traitement des CIA et reprendrons certains points afin de permettre la compréhension des traitements des données expérimentales.
5.1. Représentation du diagnostic par un vecteur de S-K-E
5.1.1. Le modèle S-K-E
Le modèle S-K-E, détaillé dans (Michelet et al., 2012b), représente des compétences (Skill en Anglais), des connaissances (Knowledge) et des erreurs (Error) en électricité. Des illustrations de S, K et E sont données dans le Tableau 1.
Nous avons ainsi choisi de discerner les entités faisant référence aux savoirs théoriques (les connaissances) de celles faisant référence aux savoir-faire qui sous-tendent un côté pratique (les compétences). Afin de différencier les différentes « origines » d’erreurs, nous en proposons une typologie en 7 catégories : erreur provenant (i) d’une non connaissance, (ii) d’une non compétence, (iii) d’un raisonnement incorrect, (iv) d’une confusion de vocabulaire, (v) d’analogie3, (vi) erreur de non-respect de la consigne ou de l’incompréhension de celle-ci, (vii) erreur due à des ambiguïtés de l’interface du système informatique.
Catégorie |
Explicitation |
Compétence (S) |
Être capable d’utiliser la loi des nœuds pour calculer l’intensité dans un circuit en dérivation. |
Connaissance (K) |
Connaître le lien entre l’état d’une DEL (diode électro luminescente) et la circulation du courant. |
Erreur (E) |
Ne pas savoir placer un fusible dans un circuit en dérivation afin qu’il protège l’ensemble du circuit. |
Tableau 1. Exemple de S, K, E
Dans notre modèle, implémenté en langage Prolog, nous avons représenté 329 entités réparties ainsi : 56 compétences, 81 connaissances et 192 erreurs. Le processus de conception du modèle S-K-E est décrit dans (Michelet, 2010).
Certaines S,K,E sont propres à une situation. Par exemple, savoir calibrer un appareil de mesure ou savoir réaliser le circuit électrique à partir d’un schéma donné sont des compétences dont la pratique ne peut être contrôlée qu’au travers l’emploi du micromonde.
5.1.2. Liste de S-K-E contradictoires
D’après notre typologie des erreurs (cf. partie 5.1.1.), des erreurs peuvent être des non connaissances ou des non-compétences, DiagElec crée ainsi une première liste de S-K-E dites contradictoires. Mais d’autres erreurs sont contradictoires : par exemple l’erreur du raisonnement séquentiel dans un circuit en série est contradictoire avec la connaissance « l’ordre des dipôles n’a pas d’importance dans un circuit série ».
Ainsi, en collaboration avec les experts, nous avons identifié parmi les S-K-E, les entités contradictoires et établi une table des contradictions possibles. Cette table est représentée à l’aide de prédicat Prolog de la forme : estContradictoire(a,b).
5.1.3. Prise en compte de l’incertitude et impact sur la personnalisation
Nous avons choisi de représenter dans le cadre de notre modèle de diagnostic, l’incertitude inhérente au diagnostic, par le biais d’un degré de croyance (DC) associé à chaque élément détecté selon l’échelle suivante :
1 = « je soupçonne que l’apprenant possède l’élément X »
2 = « je suis moyennement sûr que l’apprenant possède l’élément X »
3 = « je suis pratiquement sûr que l’apprenant possède l’élément X »
4 = « je suis sûr que l’apprenant possède l’élément X »
Ici encore nous travaillons sur le postulat que la rétroaction sera plus adaptée si le degré de croyance du système en son diagnostic est élevé. En effet, si le diagnostic est peu sûr qu’un apprenant maitrise une connaissance, la rétroaction pourra lui proposer un problème isomorphe afin de renforcer le diagnostic ; alors que s’il est sûr qu’un élève a commis une erreur, un contre-exemple pourra être proposé afin de déstabiliser cette erreur.
5.1.4. De la résolution de problème au diagnostic
Chaque problème de notre environnement est modélisé à l’aide de méta-données, qui sont regroupées au sein de 3 classes :
– Identification : Contient toutes les données caractérisant la résolution du problème comme l’identifiant du problème, celui des étapes le composant, la nature de l’étape (hypothèse, conclusion, expérimentation), la thématique.
– Problème : Contient toutes les données caractérisant le problème du point de vue didactique, telles son public, son degré de difficulté, la liste des connaissances et compétences ciblées, celles des principales erreurs attendues.
– Circuit : Contient toutes les données relatives au(x) circuit(s) électrique(s) accompagnant le problème telles que sa topologie, les composants présents ainsi que leurs états et leurs caractéristiques nominales.
Une description complète de la représentation des problèmes et des circuits électriques fournis à l’apprenant, à l’aide des méta-données mais aussi de leur représentation en faits Prolog, est donnée dans (Michelet, 2010).
En prenant en compte (1) des méta-données sur les problèmes même et (2) en enrichissant les traces brutes à l’aide du modèle SKE, le système construit des traces complétées. Le diagnostic cognitif de l’apprenant est ensuite construit à partir de ces traces.
Une description détaillée des traces brutes complétées, ainsi que des processus de transformation sont exposés dans (Michelet et al., 2012a). À partir de toutes ces données et des règles de diagnostic, l’algorithme de diagnostic est lancé afin de calculer le diagnostic de l’activité d’un apprenant selon la procédure illustrée dans la Figure 6.
Lorsqu’une règle est déclenchée, l’algorithme ajoute de manière automatique un fait signifiant que l’élément de connaissance a été détecté pour l’apprenant avec un degré de croyance.
Le diagnostic fourni par notre modèle, nommé DiagElec, prend la forme d’un vecteur de diagnostic V défini par un ensemble de Couples (Élément détecté, DegréCroyance). Par exemple, le vecteur de diagnostic VA1-P2-TPElec-DiagElec = {(k11,3),(e7,2),(s6,4),(s21,1)} représente le diagnostic réalisé par DiagElec concernant l’apprenant A1 pour le problème P2 dans le contexte de diagnostic TPElec. DiagElec est un diagnostic à base de règles implémentées en langage Prolog.

Figure 6. DiagElec : Schéma fonctionnel
5.2. Prise en compte des MRP et du contexte
5.2.1. Définitions préliminaires
Soient Q, F et T désignant respectivement les MRP : QCM, Formulation, TPElec. A partir de ces 3 MRP, nous pouvons constituer les 7 contextes de diagnostic, noté δ, suivants : Q, F, T, Q+F, Q+T, F+T, Q+F+T où pour chaque contexte, seules les traces provenant des MRP le composant sont considérées dans le diagnostic.
Nous avons vu que les problèmes proposés étaient décomposables en étapes (cf. § 4.2.). Nous appelons production élémentaire d’un problème la résolution d’une des étapes du problème, et thématique un ensemble de problèmes à traiter enchaînés de façon logique.
5.2.2. Règles de diagnostic
Les règles de diagnostic sont basées sur un ensemble de faits et de règles modélisant les connaissances, compétences et erreurs en électricité (courant continu). Cette modélisation a été réalisée à partir d’une étude d’une dizaine de manuels scolaires et des résultats issus de travaux de la didactique de la physique.
Les règles de diagnostic sont dépendantes de la MRP, elles décrivent comment détecter, pour une MRP spécifique, une connaissance, une compétence ou une erreur. La forme générale en langage Prolog d'une règle de diagnostic est la suivante :
conception (Id_MRP, Id_Pb, Id_Etape, Id_Circuit,Id_Circuit, Id_Apprenant, DC, NumRep) :-liste de conditions.
où :
_ Id_MRP : désigne la MRP ou la combinaison de MRP
– Id _Pb : désigne l’identifiant du problème
– Id_Etape : désigne l’identifiant de l’étape du problème
– Id_Circuit : désigne l’identifiant du circuit associé au problème
– Id_SKE : désigne l’identifiant de la S, K ou E
– Id Apprenant : désigne l’identifiant de l’apprenant
– DC : désigne le degré de croyance
– NumRep : désigne le numéro de l’occurrence de la réponse de l’apprenant
– Liste de conditions : désigne une liste de faits déclenchant la règle
Lorsqu’une règle est déclenchée, des faits additionnels sont ajoutés de manière dynamique afin de mémoriser la S, K ou E détectée chez l’apprenant.
Par exemple, si on considère la MRP micromonde et l’activité présentée dans la Figure 5(b), la règle traduisant la suspicion (DC=2) de l’emploi d’un raisonnement séquentiel lorsque l’apprenant connecte un interrupteur entre les 2 lampes est la suivante :
conception(tpelec,Id_Pb,Id_Etape,Id_Circuit,e121,Id_Apprenant,2,NumRep) :-
etatCircuit(tpelec,Id_Apprenant, Id_Pb,Id_Etape,Id_Circuit, ,NumRep,ferme),
presenceComposant(tpelec,Id Apprenant, Id_Pb, Id_Etape,Id_Circuit, NumRep, Id_Compo1,generateur, NomCompo1),
presenceComposant(tpelec,Id Apprenant, Id_Pb, Id_Etape,Id_Circuit, NumRep, Id_Compo2,lampe, NomCompo2),
presenceComposant(tpelec,Id Apprenant, Id_Pb, Id_Etape,Id_Circuit,NumRep, Id_Compo3,lampe, NomCompo3),
presenceComposant(tpelec,Id Apprenant, Id_Pb, Id_Etape,Id_Circuit, NumRep, Id_Compo4,interrupteur, NomCompo4), !.
5.2.3. Notations préliminaires

5.2.4. Les étapes de l’algorithme de diagnostic
Pour un apprenant A, l’algorithme considère toutes ses productions élémentaires chronologiques afin de calculer Diagnostic(A,δ) selon les différents paramètres, et se déroule ainsi :

Dans la dernière étape de l’algorithme, le Diagnostic(A, δ), est calculé en considérant l’ensemble des diagnostics des productions mais aussi en balayant à nouveau les règles. En effet, lorsqu’on considère 2 productions, le diagnostic de ces 2 productions n’est pas uniquement l’union des diagnostics de chaque production, il faut aussi balayer encore une fois l’ensemble des règles en considérant l’union de deux listes de faits associés à chacune d’elles, car cette association peut faire apparaitre de nouvelles entités diagnostiquées (un exemple est donné à travers la Figure 7 et est expliqué dans le paragraphe ci-après). Une fois, tous les diagnostics établis, DiagElec les réajuste en proportion des poids α et γ, et en tenant compte aussi des poids λ et β.
Considérons l’exemple exposé dans la Figure 7 et étudions les différentes réponses de l’apprenant, leur combinaison et leur diagnostic :
Diagnostic de la formulation 1 : L’apprenant indique que la boite noire contient un interrupteur fermé, ce qui constitue une bonne réponse. En effet, la lampe L1 étant allumée et le circuit étant en série, cela implique que le circuit électrique est fermé. Ainsi, l’apprenant maîtrise les conditions de circulation du courant dans un circuit.
Diagnostic de la formulation 2 : L’apprenant indique le courant va dans la lampe L1 (qui s’allume) mais n’arrive pas à atteindre la lampe L2, qui de ce fait, ne s’allume pas. Cette réponse est typique d’un raisonnement séquentiel où le circuit n’est pas analysé dans sa globalité mais bout à bout.
Diagnostic des 2 formulations : L’analyse des 2 formulations va permettre de diagnostiquer d’une part un raisonnement de type séquentiel et d’autre part, une inversion du rôle des interrupteurs. L’apprenant pense qu’un interrupteur fermé ne laisse pas passer le courant, ou du moins après lui.
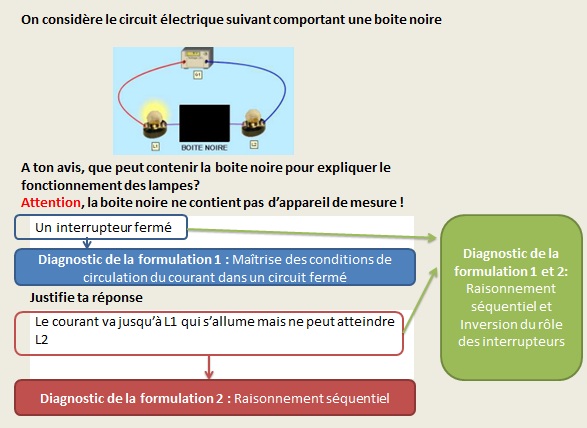
Figure 7. Illustration de l’évolution du diagnostic selon la prise en compte de tout ou partie des productions de l’apprenant
5.3. Prise en compte des CIA : étapes de l’algorithme de diagnostic
Aux notations introduites dans les parties 5.2.1. et 5.2.2., nous rajoutons les notations suivantes :
- Cl une entité diagnostiquée de degré de croyance DCCl,
- MCl la MRP qui a permis la détection de l’entité et
- Cl le poids associé à cette MRP, tel que la somme des poids vaille 100%
Soient Pi(A,Pb,M) et Pj(A,Pb,M) deux productions élémentaires de diagnostics respectifs Diagnostic(Pi(A,Pb,M)) et Diagnostic(Pj(A,Pb,M)).
Soit ListeContradictionPi(A,Pb,M) ⊎ Pj(A,Pb,M) la liste des S-K-E contradictoires des diagnostics Diagnostic(Pi(A,Pb,M)) et Diagnostic(Pj(A,Pb,M)) obtenus par parcours de la table des contradictions.
SI ListeContradictionPi(A,Pb,M) ⊎ Pj(A,Pb,M) = ∅ ALORS
1.1. Il n’y a aucune S-K-E contradictoire
⬄∀l/ Cl ⊂ Diagnostic(Pi(A,Pb,M)) ∩ Diagnostic(Pj(A,Pb,M)) = ∅ ⇒
i) Cl ⊂ DiagnosticPi(A,Pb,M) ⊎ Pj(A,Pb,M)
ii) DC(Cl) = Moyenne (αCl × DC(Cl))
1.2. ∀l/ Cl ⊂ (Diagnostic(Pi(A,Pb,M)) ⊕ Diagnostic(Pj(A,Pb,M)) ) où ⊕ désigne “Ou exclusif”
i) Cl ⊂ DiagnosticPi(A,Pb,M) ⊎ Pj(A,Pb,M)
ii) DC(Cl) = αCl × DC(Cl)
SINON Il existe au moins un couple de S-K-E contradictoire
2.1. ∀l/ Cl ⊆ DiagnosticPi(A,Pb,M) ⊎ Pj(A,Pb,M) ⇒on effectue les étapes décrites dans 1.1. et 1.2.
2.2. Soient Ca et Cb deux S-K-E contradictoires de degré de croyance respectifs DCCa et DCCb. Soient Ma et Mb. les deux outils ont sont apparues Ca et Cb de poids respectifs αaet αb
∀a,b/ Ca et Cb sont contradictoires
i) Ca ⊂ DiagnosticPi(A,Pb,M) ⊎ Pj(A,Pb,M)
ii) Cb ⊂ DiagnosticPi(A,Pb,M) ⊎ Pj(A,Pb,M)
iii) DC(Ca) ←αa × DC(Ca)
iv) DC(Cb) ←αb × DC(Cb)
6. Expérimentation et dispositifs expérimentaux déployés
6.1. Phase 1 : Collecte de productions d’apprenants en milieu scolaire
6.1.1. Dispositif expérimental
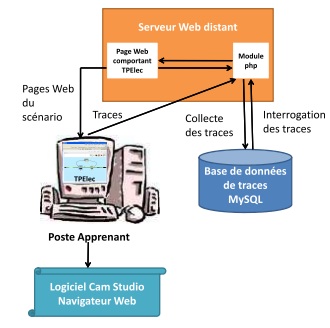
Pour réaliser notre expérimentation en milieu scolaire, nous avons créé un site Web auquel les apprenants se sont connectés afin d’exécuter le scénario pédagogique. La Figure 8(a) présente le dispositif expérimental mis en place.
6.1.2. Scénario pédagogique et population
Le scénario pédagogique proposé aux apprenants est composé de 2 activités : un QCM sur pratiquement l’ensemble des notions élémentaires en électricité et de la résolution de problèmes (où chaque problème ou étape peut faire intervenir une ou plusieurs MRP). Les problèmes sont regroupés au sein de 2 thématiques : une, T1, autour du cas d’étude classique de la Boite Noire, (Gomez et Duran, 1998), et l’autre, T2, sur les lois en électricité. Au sein de chaque classe, nous avons scindé les élèves en deux groupes : les problèmes résolus sont identiques entre les 2 groupes, seul l’ordre de passation des thématiques est inversé.
Cette phase d’expérimentation fut réalisée auprès de deux classes : une classe de quatrième et une classe de seconde comportant respectivement 25 et 35 élèves. Les élèves ont travaillé individuellement entre 90 et 120 minutes.
6.2. Phase 2 : Collecte de diagnostics faits par des experts humains
6.2.1. Tâche demandée et réduction du corpus
Afin de voir l’impact des MRP dans le diagnostic, DiagElec a effectué des diagnostics pour les 7 contextes de diagnostic. Nous avons demandé la même tâche (faire 7 diagnostics par apprenant) aux experts humains, tous enseignants certifiés ou agrégés de Sciences-Physiques (financés par l’INRP (4) dans le cadre du projet TPElec).
Au cours de la 1ère phase de l’expérimentation, nous avons collecté 1129 problèmes résolus. Ainsi, il n’était pas réalisable de demander aux experts humains de travailler sur ce corpus complet. C’est pourquoi, un algorithme de sélection d’apprenants a été mis en œuvre. Une des hypothèses que nous voulions tester était de savoir si l’ordre dans lequel étaient réalisées les activités avaient un impact sur le diagnostic, hypothèse que ni sera pas analysée dans ce texte. L’objectif de l’algorithme de sélection des élèves est de rechercher des couples d’apprenants (A1, A2) tels que A1 et A2 aient exactement les mêmes diagnostics au QCM de notions et soient dans des groupes de parcours différents. En procédant ainsi, nous avons ramené notre population à 18 apprenants et 306 problèmes résolus.
6.2.2. Dispositif expérimental
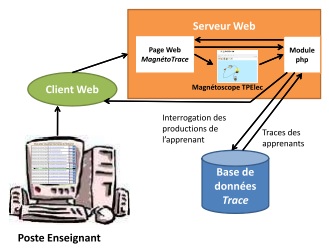
Nous avons créé un site Web MagnétoTrace permettant aux experts humains de visualiser les productions des apprenants selon un contexte de diagnostic donné. La Figure 8(b) présente le dispositif mis en place.
(a) Côté apprenant |
(b) Côté expert humain
|
Figure 8. Présentation des dispositifs expérimentaux déployés
Pour « rejouer » les actions des apprenants sur le micromonde TPElec, nous avons intégré le magnétoscope de TPElec aux pages Web. Ce magnétoscope permet à partir d’un fichier de traces TPElec, de visualiser le film des étapes successives de la construction d’un circuit, durant une activité réalisée par un apprenant sur le micromonde TPElec. Lors de l’utilisation du magnétoscope, le défilement des étapes peut se faire de manière automatique ou manuelle (pas à pas).
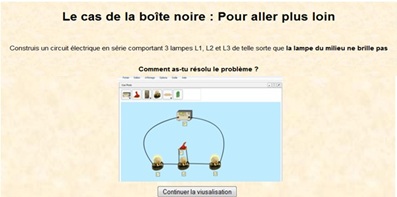
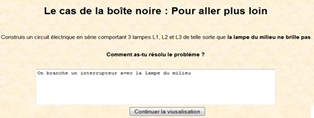
La Figure 9 présente un exemple de visualisation des productions de l’apprenant pour un même problème selon les différents contextes de diagnostic. Ce problème comporte des réponses formulées et des constructions de l’apprenant. Lorsque nous sélectionnons le contexte de diagnostic TPElec (a) ou Formulation (b), nous visualisons uniquement les traces en référence à ces contextes. Nous ne disposons pas de la réponse complète de l’apprenant, qui est visualisée uniquement lorsque les 2 modalités sont sélectionnées (c). De plus, à la fin d’un problème, l’expert humain effectue un diagnostic du problème dans sa globalité.
(a) TPElec |
(b) Formulation textuelle |
(c) Formulation textuelle + TPElec |
Figure 9. Visualisation des productions d’un apprenant selon le contexte de diagnostic
Les diagnostics issus des experts humains ont été recueillis lors d’entretiens individuels (146 heures d’enregistrement). Le protocole fut le suivant : l’expert a visualisé les données, en verbalisant son diagnostic en terme de S, K et E, en donnant pour chaque entité diagnostiquée une valeur du degré de croyance associé. Le chercheur a saisi sur un autre ordinateur ces données, en synchrone ou asynchrone.
7. Résultats et analyse
Nous évaluons tout d’abord la pertinence des diagnostics émis par DiagElec en les comparants à ceux réalisés par les experts humains. Ensuite, dans les paragraphes suivants, nous nous concentrons autour des MRP et des CIA. En effet, notre objectif est de voir et mesurer l’impact (1) de la prise en compte des MRP dans le diagnostic ainsi que la valeur ajoutée de chaque MRP, (2) du contexte de résolution. De plus, concernant la détection des CIA et leur traitement, nous comparons le comportement de DiagElec et celui des experts sur des études de cas.
Préalablement à la présentation des résultats et de l’analyse s’y référant, nous introduisons les notions de vecteur de degré de croyance et de convergence humaine. Nous désignons par E1, E2, E3 les experts humains et par E4 DiagElec.
7.1. Définitions préliminaires
7.1.1. Vecteur de diagnostic et de degré de croyance
Pour un apprenant, un problème et une MRP donnés, nous disposons de 4 vecteurs de diagnostic, un par expert, comme le montre la Figure 10. Ainsi, par exemple, l’expert E1 a diagnostiqué que l’élève A1, dans la résolution du problème P2 et en considérant uniquement la MRP TPElec, possède la connaissance k11 avec un degré de croyance de 2, l’erreur e7 avec un degré de croyance de 3 et la compétence s6 avec une degré de croyance de 4.
`
Figure 10. Exemple de quadruplet de vecteurs de diagnostic
À partir de ces vecteurs, nous construisons un vecteur de degré de croyance, noté V_DegréCroyanceA-P-C-D composé des DC mis respectivement par E1, E2, E3, E4 et ceci, pour une S, K, E donnée. Nous assignons la valeur 0 au DC d’un expert pour indiquer que pour ce dernier la S, K ou E impliquée ne figurait pas dans son vecteur de diagnostic. Concrètement, à partir des vecteurs de la Figure 10, nous obtenons les vecteurs de DC de la Figure 11. Nous avons obtenu au total 19901 vecteurs de DC.

Figure 11. Exemple de vecteur de degré de croyance
7.1.2. Convergence humaine
Pour chaque élément détecté, nous calculons, à partir de chaque V_DegréCroyance, les distances un à un des degrés de croyance des experts humains que nous désignons respectivement par d1, d2 et d3, (d1 étant la distance entre E1 et E2). Nous définissons la convergence humaine entre experts humains ainsi :

Le tableau 2 donne une illustration du traitement, où DCEi représente le DC mis par l’expert Ei. Lorsque pour un élément détecté la convergence humaine est totale nous introduirons la notion de méta-expert humain.
S-K-E |
DCE1 |
DCE2 |
DCE3 |
d1 |
d2 |
d3 |
Valeur de cGlobaleHumaine |
Catégorie d’accord inter-expert humain |
k10 |
0 |
0 |
2 |
0 |
0 |
-2 |
0.667 |
Divergence |
k11 |
2 |
3 |
4 |
-1 |
-2 |
-1 |
0.816 |
Divergence |
s6 |
4 |
4 |
4 |
0 |
0 |
0 |
0 |
Convergence Totale |
s21 |
0 |
1 |
0 |
-1 |
0 |
1 |
0.471 |
Convergence Partielle |
e7 |
3 |
2 |
4 |
1 |
-1 |
-2 |
0.816 |
Divergence |
e14 |
0 |
0 |
1 |
0 |
-1 |
-1 |
0.471 |
Convergence Partielle |
Tableau 2 • Illustration des catégories de convergence humaine
La Figure 12 synthétise cette évaluation.

Figure 12. Synthèse du comportement de DiagElec et des experts humains
7.2. Impact de la prise en compte des MRP
Nous considérons dans cette étude l’ensemble des 19 901 vecteurs de croyance, et, nous nous concentrons sur le nombre de connaissances, compétences et erreurs détectées chez au moins un expert (humain ou automatique). Les éléments de connaissance ne sont comptabilisés qu’une seule fois, même si la S-K-E est détectée chez plusieurs apprenants. La figure 13 présente pour chaque expert, le nombre total de S-K-E détectées selon le fait qu’il considère un, deux ou trois outils mis à disposition de l’apprenant. Cette figure montre que plus les experts considèrent d’outils, plus ils détectent d’entités, ce qui n’est pas surprenant car certaines entités s’expriment à travers la combinaison de modalités différentes. Nous en avons vu un exemple dans la Figure 3.
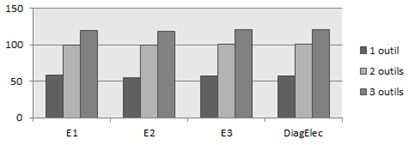
Figure 13. Détection de S-K-E de chaque expert selon le nombre
d'outils
Analysons de façon plus précise le rôle de chaque contexte dans le degré de croyance donné par l’expert. Nous considérons seulement les vecteurs où il y a convergence humaine totale. Nous comparons donc la moyenne des DC calculée pour le méta-expert humain et ceux de DiagElec selon la catégorie S, K, E. Les résultats obtenus sont présentés dans la Figure 14.
Nous constatons que c’est dans le contexte Formulation que se trouvent les DC les plus bas pour le méta-expert, mais que lorsque cette MRP est combinée avec une autre, alors le DC augmente nettement. Durant nos interviews avec les experts humains, nous les avons interrogés sur ce comportement retrouvé chez chacun d’eux, voici leur explication : « Quand je ne possède que la formulation, je n’accorde pas trop de poids à ce que dit l’élève. Cependant, quand je prends en compte la formulation et TPElec, il y a 2 situations : soit sa construction est en accord avec la formulation auquel cas j’augmente mon degré de croyance, soit sa construction n’a aucun sens et dans ce cas, je diminue le degré de croyance car je suis sûr qu’il ne sait pas la loi, il sait juste réciter ce qu’on lui a dit en classe »
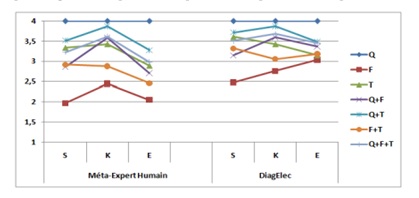
Figure 14. Comparaison des DC moyens Méta Expert humain Vs. DiagElec, selon le contexte de diagnostic et la catégorie de l’élément détecté
En nous appuyant sur ces données, nous confortons nos hypothèses, à savoir d’une part que plus le diagnostic combine d’outils, plus il s’affine dans le cas de contradictions intra-apprenants : le degré de croyance augmente ou diminue en fonction des contradictions éventuelles détectées. Nous pouvons constater qu’en présence d’une combinaison d’outils impliquant la modalité QCM, le degré de croyance va toujours diminuer. Ce comportement est dû au fait qu’une réponse dans le QCM va déclencher les règles appropriées mais toutes avec un degré de croyance maximum. Ainsi, celui-ci ne peut augmenter. D’autre part, nous observons une relation entre le contexte de diagnostic et le degré de croyance. Ainsi, la prise en compte du contexte a un impact réel sur le diagnostic.
Nous avons procédé à des études plus approfondies relatives autour de l’impact des MRP sur les DC (telles des ANOVA, de test de Chi², etc.) que nous ne développerons pas ici, puisqu’elles ont fait l’objet d’articles auxquels nous invitons le lecteur à se référer (Michelet et al., 2010a), (Michelet et al., 2010b).
7.3. Impact de la prise en compte des CIA
Nous nous sommes intéressés au cas de contradiction intra-apprenant (CIA) à travers un ou plusieurs outils. Cette étude se justifie par leur taux d’importance. En effet, nous avons fait tourner DiagElec sur les productions des 60 apprenants et nous avons relevé : 47% de CIA au sein d’une MRP, 56% entre 2 MRP et 51% entre 3 MRP. La Figure 15 explicite les pourcentages de CIA selon les MRP et où la population statistique est soit l’ensemble des 60 apprenants, soit les 18 apprenants sélectionnés. La Figure 16 donne une cartographie propre à chacun des 18 apprenants sélectionnés des détections des CIA selon les MRP.

Figure 15. Synthèse de la mise en évidence des CIA

Figure 16. Carte de détection des CIA des 18 apprenants
Sur ces figures, nous remarquons l’existence de telles situations au travers toutes les combinaisons d’une, deux ou des trois MRP mises à disposition de l’apprenant. En particulier, tous les apprenants ont manifesté au moins une CIA entre la formulation et TPElec.
La Figure 16, sur les 18 élèves observés par les enseignants, fait apparaître l’existence d’au moins une CIA de chaque catégorie (au sein d’un MRP, entre 2 MRP et entre 3 MRP) pour tous les apprenants. Ceci renforce l’idée que si nous laissons l’apprenant se contredire, le diagnostic est capable de le détecter. Nous pouvons constater que les contradictions touchent plus les formulations et les actions que les réponses à des QCM, puisque dans les deux premiers cas l’apprenant est « plus libre » de sa réponse, qui n’est pas prédéfinie.
Pour ces 18 apprenants sélectionnés, nous avons regardé l’évolution de la composition du vecteur de diagnostic en cas de CIA que ce soit chez les experts humains ou DiagElec, et selon les différents contextes : l’expert (humain ou DiagElec) garde une trace de la CIA dans leur diagnostic. Ainsi, ces études montrent que plus le diagnostic combine les traces issues de MRP d’un environnement, plus il met en lumière des contradictions intra-apprenant. Nous allons étudier la façon dont DiagElec mais aussi les experts humains traite les CIA selon les différents contextes de leur apparition.
7.3.1. Traitement des CIA, étude des cas
Dans la suite, nous avons procédé à des études de cas afin de confronter le comportement de DiagElec et celui des experts humains. Pour ce faire, nous avons pour chaque catégorie (CIA au sein d’une – deux –trois MRP) 1) analysé les productions de l’apprenant pour voir l’existence de CIA, 2) comparé le traitement de la CIA par DiagElec et par les experts humains 3) analysé l’évolution du diagnostic qu’il soit émis par DiagElec ou par les experts humains.
Nous ne détaillerons pas toutes les études de cas des CIA. Nous invitons le lecteur à se référer au chapitre 16 de (Michelet, 2010). Néanmoins, nous présentons notre processus de méthodologie sur une étude de cas : le cas de l’apprenant A2 pour lequel nous avons détecté des CIA entre les 3 MRP. La Figure 17 présente l’évolution de son diagnostic.

Figure 17. Evolution du diagnostic de l’apprenant A3 en cas de CIA
Ainsi :
– La connaissance k31 a été détectée par chacun des experts en visualisant les productions de cet apprenant dans la Formulation (F) et dans TPElec (T). Ainsi, elle apparaît dans le diagnostic combinant les 3 MRP (Q+F+T).
– L’erreur e52a (qui est en contradiction avec la connaissance k31) a été détectée par chacun des experts en visualisant les productions de cet apprenant dans le QCM (Q) mais aussi dans TPElec (T). Cette erreur apparaît dans le diagnostic combinant les 3 MRP (Q+F+T).
Nous pouvons voir dans ce cas que les trois experts humains ont diminué le degré de croyance à propos de la connaissance qui est contradiction avec l’erreur une fois que les trois contextes ont été observés.
Ainsi à partir de l’analyse des traces, sur les 18 élèves, nous avons fait apparaitre différents comportements selon le contexte dans lequel apparait la CIA.
CIA au sein d’une MRP. Nous constatons des convergences mais aussi des divergences entre le comportement de DiagElec et celui des experts humains. En effet, selon le type de MRP les experts humains conservent dans leur diagnostic final la trace de S-K-E contradictoires (c’est le cas pour les QCM et TPElec) alors que dans le cas de la Formulation, ils n’en conservent qu’une : soit la connaissance/compétence, soit l’erreur associée. Alors que DiagElec conserve une trace de S-K-E contradictoires, et ce quelle que soit la MRP.
Ce constat peut s’expliquer par le fait qu’au sein d’un problème, une seule construction est demandée alors que plusieurs étapes faisant appel à de la Formulation apparaissent et que celles-ci n’ont pas le même poids pour les experts humains. En effet, il y a une influence sur le diagnostic selon que la formulation d’une réponse à une étape est faite avant ou après la construction du circuit. Nous en déduisons que nous devons, dans nos perspectives, attribuer des poids différents aux réponses d’étapes au sein d’un même problème.
CIA entre deux MRP. Les experts humains, en cas de contradiction entre QCM et un autre outil, accordent toute confiance soit à la Formulation, soit à TPElec et la réponse au QCM est ainsi jugée sans intérêt. Ceci montre le poids très faible que les experts humains attribuent à des réponses issues de QCM. À contrario, DiagElec conserve une trace des contradictions et ne met pas de côté les diagnostics établis suite à des réponses de nature QCM.
Dans le cas d’une contradiction entre la Formulation et TPElec, l’expert (humain ou automatique) conserve des S-K-E contradictoires dans le diagnostic final. Ainsi, cela montre l’importance de ces 2 MRP : une MRP n’est pas négligée par rapport à une autre. Néanmoins, si nous considérons les couples (S-E) ou (K-E) contradictoires, trois comportements émergent, et ce quel que soit l’expert :
(a) Si la contradiction a eu lieu dans deux MRP distinctes (ie. S ou K détectée uniquement dans une MRP et E détectée uniquement dans l’autre) : le DC reste stable. Ceci montre que les experts n’accordent pas plus de poids à la formulation qu’à TPElec ou vice-versa.
(b) Si S ou K a été détectée dans les 2 MRP et E uniquement dans une : le DC de la connaissance ou compétence augmente et le DC de l’erreur diminue, et ceci, quelle que soit la MRP où a été détectée l’erreur.
(c) Si E a été détectée dans les 2 MRP et S ou K uniquement dans une : augmentation du DC de l’erreur et diminution du DC lié à la connaissance ou compétence, ceci, quelle que soit la MRP où a été détectée la connaissance ou compétence.
Une des interprétations possible est qu’en cas de contradictions entre la Formulation et TPElec, ce n’est pas la nature même de l’outil qui a un poids, mais le nombre d’outils entrant en jeu dans la détection de la S, K ou E, et ce quel que soit l’expert. Une autre interprétation étant liée à la fréquence relative de l’apparition de l’erreur par rapport à la connaissance ou compétence.
CIA entre trois MRP. Dans le cas de contradiction détectée à travers l’utilisation des 3 MRP, nous constatons que :
– Tous les experts gardent une trace des S, K et E contradictoires relevées au cours de la résolution de problèmes chez l’apprenant,
– Le diagnostic émis en ne considérant que la MRP QCM ne sert qu’à confirmer, pour les experts humains comme chez DiagElec, un diagnostic émis en ne considérant que la Formulation, ou TPElec. Il ne sert jamais à invalider un diagnostic émis en ne considérant que ces deux dernières MRP. Ceci montre là encore, le faible poids attribué aux réponses à des QCM.
– Pour les experts humains, l’outil Formulation n’est pas prépondérant sur l’outil TPElec, ou vice-versa. Ces MRP sont considérées avec le même poids chez les experts humains (sauf dans un cas sur 14 où TPElec ”prédomine” sur la Formulation).
CIA et poids des MRP. Nous nous sommes ensuite intéressés au poids des MRP les unes par rapport aux autres en cas de CIA. Pour cela, nous avons procédé, pour les 18 apprenants et toutes les combinaisons de CIA, à des études de cas en observant le comportement 1) des experts humains, 2) de DiagElec sur l’évolution d’un diagnostic et des DC des entités détectés. Nous avons dans un dernier temps comparé les comportements humains/machine. Nous aboutissons à la conclusion suivante : Quel que soit l’expert (humain ou DiagElec), en cas de contradiction entre les MRP Formulation et TPElec, ces MRP n’ont pas le même poids selon la catégorie de l’élément détecté. Par exemple, si une compétence est mise en jeu, tous accordent plus de poids à l’outil TPElec. De même, si une connaissance est mise en jeu, tous accordent plus de poids à l’outil Formulation.
Lorsque la MRP QCM entre en jeu, aucun expert (humain ou DiagElec) ne lui confère de poids. Concrètement entre une réponse juste (respectivement fausse) à un QCM et une action ou formulation erronée (resp. correcte), telle qu’il existe un lien entre ces S-K-E, c’est toujours le diagnostic de l’action ou de la formulation qui est conservé, celui lié au QCM étant mis de côté. Le comportement des enseignants peut être expliqué par le peu de confiance qu’ils attribuent aux QCM. Leurs reproches concernant cette modalité sont, entre autres : question fermée, effet de hasard, présence de la réponse correcte pouvant activer un sentiment de déjà-vu chez l’élève (qui choisit ainsi la bonne réponse, mais aurait été incapable de la fournir si elle ne lui avait pas été suggéré). Ainsi, ce constat peut nous amener à réfléchir quant à l’utilisation unique de QCM dans le calcul du diagnostic. Ce constat rejoint d’autres émis dans la littérature : « Interpréter le comportement de l’apprenant en termes de compétences ou connaissances nécessite des connaissances liées à la situation d’apprentissage mise en œuvre dans l’EIAH, et des techniques informatiques pointues si l’on souhaite travailler à partir d’activités riches ne se résumant pas à des QCM, afin de permettre aux apprenants d’exprimer pleinement leurs connaissances. » (Leroux et Jean-Daubias, 2007, p. 121), « Ce souci d’usage [...] retrouve tout d’abord à travers la recherche d’une fiabilité maximale des observables (qui ne peuvent pas se limiter à des QCM) sans laquelle le diagnostic ne peut être fiable. » (Jean-Daubias, 2002, p. 172).
8. Discussions et Perspectives
Du point de vue de la modélisation, nous pouvons conclure que le modèle d’élève proposé (S, K, E) ainsi que le fait de considérer plusieurs MRP dans le processus de diagnostic permet d’identifier des comportements de type CIA. Comme le diagnostic cognitif est un processus empirique basé, entre autres, sur l’analyse comportementale de l’apprenant, il semble donc pertinent de prendre en compte les CIA pour que le diagnostic soit au plus près du comportement de l’apprenant.
L’apport de notre travail est la proposition d’un diagnostic informatique combinant plusieurs modalités d’expression de connaissances et tenant compte du contexte de leur expression pour établir un diagnostic.
Du point de vue de l’implémentation du modèle, la détection de CIA se fait en proposant des prédicats construits à partir d’analyses expertes. Cette démarche ne garantit pas la complétude et demande une analyse de connaissance du domaine. Par contre l’algorithme de traitement est générique : ajouter de nouvelles connaissances au système ne nécessite que l’analyse des connaissances du domaine. Par ailleurs, construire des faits Prolog, et non seulement des prédicats permettait de rendre plus générique la démarche.
Une fois les CIA détectées, dans un système d’apprentissage elles peuvent être traitées de deux façons que ce soit au niveau du diagnostic ou de la rétroaction. Au niveau de la rétroaction, le postulat est que le fait d’avoir identifié une contradiction rendra possible la proposition d’une situation permettant à l’apprenant de surmonter cette contradiction. Nous avons produit des règles pouvant tracer ces contradictions, première étape indispensable pour qu’un EIAH produise les rétroactions adaptées (Brusilovsky et Peylo, 2003), (Keenoy et al., 2007).
Au niveau du diagnostic, nous avons analysé le rôle des contextes de diagnostic dans le traitement des CIA identifiées. Ainsi, notre expérimentation conforte l’idée que la prise en compte des traces provenant de tous les outils mis à disposition de l’apprenant permet un diagnostic plus fin que sans cette considération. Nous avons recherché de façon plus précise l’influence de chaque contexte dans le processus de diagnostic, en particulier dans le cas des contradictions intra-apprenant. Ainsi, le contexte a une influence sur la nature des éléments détectés (S, K ou E), facteur qui peut s’avérer très significatif en cas de CIA car, selon la nature des éléments de connaissance ciblés, nous savons à quelle MRP accorder plus de poids lors de l’établissement du diagnostic. Le diagnostic nécessite des raisonnements qui considèrent non seulement la MRP mais aussi le type de problème ainsi que les éléments ciblés par ce problème.
Par ailleurs, une autre perspective qui nous parait intéressante à explorer est la prise en compte de l’incertitude du point de vue de l’apprenant. En effet nous avons intégré la dimension d’incertitude du point de vue du diagnostic fait par l’expert humain. Nous pensons que pour affiner et enrichir le diagnostic, mais également la personnalisation, il peut être aussi intéressant que l’apprenant puisse exprimer le degré de croyance qu’il donne à sa formulation. Prendre en compte l’incertitude côté apprenant est préconisée par certains auteurs (Jans et Leclercq, 1999).
Enfin, pour aller dans le sens de l’adaptation et de la personnalisation dans le cas des CIA, il nous semble important d’aborder la question de la rétroaction à partir des résultats produits par le système de diagnostic présenté dans ce papier. En effet, la perspective de ce point de vue est de concevoir un système de rétroaction adaptatif qui prenne en compte le résultat du diagnostic ainsi que les CIA détectées.
Bibliographie
ASTOLFI, J.P., DAROT, E., GINSBURGER-VOGEL, Y., TOUSSAINT, J. (1997). Mots-clés de la didactique des Sciences. Collection Pratiques Pédagogiques. De Boeck Université (Eds.).
BALACHEFF, N. (1994). Didactique et intelligence artificielle. Recherches en didactique des mathématiques , Vol. 14 n°1, p. 9-42.
BLONDEL F.M., SCHWOB M., TARRIZO M. (1997). Diagnostic et aide dans un environnement d’apprentissage ouvert : un exemple en chimie SCHNAPS. Revue Sciences et Technologies Educatives, Vol 4 n°4, p. 1-34.
BOUZEGHOUB M., KOSTADINOV D. (2005). Personnalisation de l'information : aperçu de l'état de l'art et définition d'un modèle flexible de définition de profils. CORIA’2005, p. 201-218.
BRUSILOVSKY P., PEYLO C. (2003). Adaptive and Intelligent Web-based Educational Systems. International Journal of Artificial Intelligence in Education, Vol. 13 n°2-4 p.159–172.
BUTOIANU V., VIDAL P., VERBERT K., DUVAL E., BROISIN J. (2010) User context and personalized learning: a federation of Contextualized Attention Metadata, Journal of Universal Computer Science, Vol. 16 n°16 p. 2252-2271.
CALMETTES, B. (2009). Milieu didactique et démarches d’investigation. Actes du premier Colloque International de l’ARCD « Où va la didactique comparée ? ». GENÈVE (Suisse) : ARCD.
CLUSTER ISLE. (2009). Projet “Personnalisation des EIAH” http://liris.cnrs.fr/~clu-eiah/
CORBETT A.T., ANDERSON J. (1995) Knowledge tracing: modeling the acquisition of procedural knowledge. User Modeling and User Adapted Interaction, Vol. 4, p. 253-278.
DERRY, S., HAWKES, L., KEGELMANN, H., HOLMES, D. (1989). Fuzzy remedies to problems in diagnostic modeling. In Bierman, D., Breuker, J., and Sandberg, J., editors, 4th International conference on AI and Education, Amsterdam, p. 81–85. IOS, Amsterdam
de VECCHI, G. (2006). Enseigner
l’expérimental en classe : pour une véritable
éducation scientifique. Paris : Hachette Education (Eds.).
D’HAM C., MARZIN P., WAJEMAN C. (2009) SCY-Science Created by you: an
online environment for inquired-based and design-based learning. First
Workshp on the S-team European Project.
GILMORE, D., SELF, J. (1998). The application of machine learning to intelligent tutoring systems. In J. Self (ed.): Artificial Intelligence and Human Learning: Intelligent Computer-Aided Learning. London: Chapman and Hall, p. 179-196.
GIORDAN A. (1999). Une didactique pour les sciences expérimentales, chapitre « Epistémologie de la démarche expérimentale », p. 48–57. Belin, Paris (Eds.).
GOGUADZE G., MELIS E. (2009) Combining Evaluative and Generative Diagnosis in ActiveMath. In Artificial Intelligence in Education. p. 668-670. Brighton: IOS Press.
GOMEZ E., DURAN E. (1998) Didactics Problems in the
concept of electric potential difference and an analysis of its philogenesis. Science and Education. Vol.![]()
![]() 7 p. 129-141.
7 p. 129-141.
HAUSMANN RG., de SANDE BV., VanLEHN K. (2008). Shall we explain? Augmenting learning from Intelligent Tutoring Systems and Peer Collaboration, ITS’08, p. 636–645.
HEILI J., OLLAGNIER-BELDAME M. (2008). Traces d’utilisation, utilisation de traces : Application à l’adaptation des IHM. Colloque de l’Association Information & Management 9 pg.
HIBOU M., PY D. (2006). Représentation des connaissances de l’apprenant. Dans Environnements Informatiques pour l’apprentissage Humain, chapitre 4, Hermès-Lavoisier, p. 97-116.
HOC J., AMALBERTI R. (1992). Diagnostic et prise de décision dans les situations dynamiques. Psychologie Française, Vol. 39 p. 177–192.
IQBAL A., OPPERMANN R., PATEL A., KINSHUK. (1999). A classification of Evaluation Methods for Intelligent Tutoring Systems, Software-Ergonomie’99, p. 169–181.
JANS V., LECLERCQ D. (1999). Mesurer l’effet de l’apprentissage à l’aide de l’analyse spectrale des performances, L’évaluation des compétences et processus cognitifs, p. 303–317.
JAMESON, A. (2003). Adaptive Interfaces and Agents, In J. A. Jacko & A. Sears (Eds.), The human-computer interaction handbook: Fundamentals, evolving technologies and emerging applications (p. 305–330). Mahwah, NJ: Erlbaum.
JEAN-DAUBIAS S. (2002). Un système d'assistance au diagnostic de compétences en algèbre élémentaire, Revue STE - Sciences et techniques éducatives Vol. 9 n°1-2, p. 171-200, Hermès.
JONASSEN D., GRABOWSKI B. (1993). Handbook of individual differences, learning, and instruction. Lawrence Erlbaum Associates Publishers, Hillsdale, New Jersey Hove and London.
KEENOY K., LEVENE M., De FREITAS S. (2007). Personalised Trails: How machine can learn to adapt their behaviour to suit individual learners, Technology Enhanced Learning, Special on Trails in Education, Sense publishers, Vol. 1 p. 33-58.
LABORDE JM. (1995). Intelligent Microworlds and Learning Environments, Nato Asi Series, Berlin: Springer Verlag, p. 113-132.
LAROUSSI M., CARON PA. (2010). EIAH adaptatif et style d’apprentissage : les possibilités du web 2.0, Journée Conception des EIAH à l’ère du Web2.0 et à l’aube du Web 3.0, 8 pg.
LEROUX P., JEAN-DAUBIAS S. (2007). EIAH partenaires des acteurs de la situation d'apprentissage. Environnements informatisés et ressources numériques pour l'apprentissage : conception et usages, regards croisés, sous la direction de M. Baron, D. Guin, L. Trouche, Hermès-Lavoisier, chapitre 4, p. 107-136.
LUENGO V. (2005). Some didactical and epistemological considerations in the design of educational software : the Cabri-Euclide example. International Journal of Computers for Mathematical Learning, Vol. 10 p. 1–29. Kluwer Academic (Eds.).
LUND K., MILLE A. (2009). Analyse de traces et Personnalisation des EIAH, chapitre 1 : Traces, Traces d’interactions, Traces D’apprentissages Définitions, Modèles Informatiques, Structurations, Traitements et Usages Lavoisier-Hermès : Paris, p. 1–46.
MAYO M., MITROVIC A. (2001). Optimising ITS behaviour with bayesian networks and decision theory. International Journal of Artificial Intelligence in Education, Vol. 12 p. 124-153.
MICHELET S. (2005). Étude d’un environnement pour le diagnostic et la remédiation de conceptions erronées en électricité. Mémoire de D.E.A., Université Grenoble II.
MICHELET S. (2010). Modélisation et conception d’un diagnostic informatique prenant en compte plusieurs modalités de résolution de problèmes dans un EIAH en Electricité, Thèse de doctorat, Spécialité Ingénierie de la Communication Personne-Système, Université de Grenoble.
MICHELET S., LUENGO V., ADAM J.M. (2006). Un questionnaire dynamique pour le suivi et l'analyse de l'activité et des productions d'élèves en électricité. JOCAIR’2006, p. 421-434.
MICHELET S. ADAM J.M., LUENGO V. (2007). Adaptive learning scenarios for detection of misconceptions about electricity and remediation. International Journal of Emerging Technologies in Learning, Vol. 2, n°1. 5 pages.
MICHELET S., LUENGO V., ADAM J.M., MANDRAN N. (2010a). How to take into account different problem solving modalities for doing a diagnosis? Experiment and results, ITS’2010 Bridges to Learning, V. Aleven, J. Kay and J. Mostow (Eds), Springer-Heidelberg, p. 380-383, USA.
MICHELET S., LUENGO V., ADAM J.M., MANDRAN N. (2010b). Experimentation and results for calibrating automatic diagnosis belief linked to problem solving modalities: a case study in electricity, ECTEL’2010, M. olpers et al. (Eds.), p. 408-413, Springer-Verlag Berlain Heildelberg.
MICHELET S., LUENGO V., ADAM J.M., MANDRAN N. (2012a). Interpréter automatiquement des traces d’activités d’apprenants issues de différents contextes dans une visée de diagnostic – Etude de cas : le modèle DiagElec, Revue Ingénierie des Systèmes d'Information, Spécial « Traces, Contexte, Interaction », Vol. 17, n 2, p. 41-72, Hermès-Lavoisier.
MICHELET S., LUENGO V., ADAM J.M.,(2012b). De la conception à l’évaluation d’un modèle pour le diagnostic des connaissances - Etude de cas : le modèle S-K-E, IC’2012, 23èmes journées francophones d'Ingénierie des Connaissances, 24-29 Juin 2012, Paris, 16 pages.
MUFTI-ALCHAWAFA D. (2008). Modélisation et représentation de la connaissance pour la conception d’un système décisionnel dans un EIAH en chirurgie. Thèse de doctorat, Grenoble.
OHLSSON S. (1992) Constraint based student modeling. Artificial Intelligence and Education, Vol. 3 n°4, p. 429-447.
RASMUSSEN J. (1986). Information Processing and Human-Machine Interaction: An Approach to Cognitive Engineering. Elsevier Science Inc. New York, USA.
RAZZAQ, L., HEFFERNAN, N.T. (2008). Towards Designing a User-Adaptive Web-Based E-Learning System. In Mary Czerwinski, Arnold M. Lund, Desney S. Tan (Eds.): Extended Abstracts Proceedings of the 2008 Conference on Human Factors in Computing Systems, CHI 2008, p. 3525-3530. Florence, Italy: ACM.
SEHABA K., ENCELLE B., MILLE A. (2009). Adaptive Technology-Enhanced Learning based on Interaction Traces. AIED’09, Workshop “Towards User Modeling and Adaptive Systems for All: Modeling and Evaluation of Accessible Intelligent Learning Systems”.
SIMONIN, J., CARBONELL, N. (2007). Interfaces adaptatives : adaptation dynamique à l’utilisateur courant. In Saleh, I. and Regottaz, D., Interfaces numériques, Paris : Hermès Lavoisier (coll. Information, hypermédias et communication).
VAN JOOLINGEN, W. R., & de JONG, T. (2003). SimQuest: Authoring educational simulations. In T. Murray, S. Blessing & S. Ainsworth (Eds.), Authoring tools for advanced technology educational software: Toward cost-effective production of adaptive, interactive, and intelligent educational software (p. 1-31). Dordrecht: Kluwer Academic Publishers.
VAN LEHN K. (1988). Student modeling, Foundations of Intelligent Tutoring Systems, Polson & Richardson (Eds.), Lawrence Erlbaum Associates Ltd., Hove.
VAN LEHN K., LYNCH C., SCHULZE K., SHAPIRO J.A., SHELBY R., TAYLOR L., TREACY D., WEINSTEIN A., WINTERSGILL M. (2005). The Andes Physics Tutoring System: Lessons Learned, International Journal of Artificial Intelligence and Education, Vol. 15 n°3, p. 147-204.
VASSILEVA J. , McCALLA, G., GREER, J. (2002). Multi-agent Multi-user modelling in I-help , User Modelling and User Adapted Interaction E. Andre and A. Paiva (Eds.), Special Issue on User Modelling and Intelligent Agents, 29 pg.
VEZIAN N. (2008). Adaptation dynamique d’interface pour le suivi en temps réel d’apprenants. Rencontres doctorales de la conférence IHM 2008, p.41–44.
VIENNOT, L. (1996) Raisonner en Physique. De Boeck Université (Eds.).
WEBBER C., BERGIA L., PESTY S., BALACHEFF N. (2001). The Baghera project: a multi-agent architecture for human learning. Workshop - Multi-Agent Architectures for Distributed Learning Environments. International Conference on AI and Education.
WENGER, E. (1987). Artificial intelligence and tutoring systems: computational and cognitive approaches to the communication of knowledge. Morgan Kaufman Publishers.
 A
propos des auteurs
A
propos des auteurs
Sandra MICHELET est docteur en ingénierie de la communication personne-système de l'Université de Grenoble. Après avoir travaillé au sein de l'équipe MeTAH (Modèles et Technologies pour l'Apprentissage Humain) du LIG (Laboratoire d'Informatique de Grenoble), elle a rejoint le pôle R&D de la société Action on Line. En parallèle de ses travaux en ingénierie pédagogique, ses recherches portent sur la modélisation des connaissances et sur le diagnostic de celles-ci dans une visée de personnalisation de l’apprentissage dans des contextes d’environnements informatiques.
Adresse : Action on Line R&D Le Contemporain, 52 chemin de la Bruyère 69574 DARDILLY CEDEX
Courriel : smichelet@action-on-line.fr
Vanda LUENGO est maître de conférence-HDR en informatique à l'Université Joseph Fourier. Elle est rattachée au LIG (Laboratoire d'Informatique de Grenoble) au sein de l'équipe MeTAH (Modèles et Technologies pour l'Apprentissage Humain). Ses recherches portent sur la modélisation informatique des interactions favorisant l’apprentissage humain dans une approche centrée connaissances. Ses thèmes d'intérêt sont le diagnostic des connaissances et la conception des rétroactions épistémiques. Ces recherches ont évolué d'une démarche centrée expert vers une démarche centrée données. Ces projets actuels sont sur la capitalisation des traces et des outils d'analyse de ces traces pour le diagnostic et la rétroaction ainsi que sur l'apprentissage des connaissances perceptivo-gestuelles et la production de rétroactions épistémiques dans des domaines mal définis.
Adresse : Bureau : 342 - Bâtiment B - Ense3- 3ème étage. 11, rue des Mathématiques. BP 46 - 38402 Grenoble Cedex
Courriel : Vanda.Luengo@imag.fr
Toile : http://membres-liglab.imag.fr/luengo/
(1) Baghera est un environnement multi agents d’apprentissage de la preuve en géométrie.
(2) Andes est un tuteur intelligent proposant à l’apprenant de résoudre des problèmes dans le domaine de la mécanique newtonienne.
(3) Nous regroupons dans cette catégorie toutes les analogies, qu’elles soient adaptées ou non, puisque la frontière entre les 2 est floue. En effet, l’analogie la plus répandue est celle du circuit hydraulique/circuit électrique qui pour certains élèves va se révéler bénéfique (en permettant de résoudre des problèmes d’intensité, de tension et résistance), et pour d’autres élèves va engendrer des confusions telles que l’électricité en tant que fluide ont une inversion du rôle des interrupteurs.
(4) Institut National de Recherche Pédagogique (INRP).
Référence de l'article :
Sandra MICHELET, Vanda LUENGO, Étude de cas : DiagElec un diagnostic informatique , Revue STICEF, Volume 19, 2012, ISSN : 1764-7223, mis en ligne le 21/11/2012, http://sticef.org

© Revue Sciences et Techniques de l'Information et de la Communication pour l'Éducation et la Formation, 2012