Sommaire

Rechercher

• auteur
• année
• titre
• résumé
• abstract
• rubrique

Contact : infos@sticef.org

Analyse de fichiers de traces d’étudiants : aspects didactiques

Fabrice Vandebrouck Equipe Didirem, Université Paris 7

Claire Cazes Equipe Didirem, L'UTES, Université Paris 6

RÉSUMÉ : Les utilisateurs d’une plate-forme d’enseignement sont logués et leurs actions enregistrées dans de multiples fichiers. Ces fichiers fournissent un matériau très conséquent. La question qui nous occupe ici est l’exploitation de ces fichiers au service de différents acteurs en relation avec la plate-forme. Nous présentons d’abord la plate-forme utilisée et les expérimentations associées. Un modèle didactique permet de passer d’une information quantitative obtenue par les premiers résultats à une analyse qualitative. La construction de deux indices conduit à une typologie simple des exercices. Nous montrons que cette typologie est stable à travers les différentes expérimentations, cohérente avec les analyses didactiques a priori. Elle permet alors d’organiser, suivant les types d’exercices, les résultats et les perspectives pour chacun des trois métiers que nous retenons ici : le concepteur de plate-forme, le didacticien et l’enseignant.Plate-forme d’enseignement, scénario a priori, analyse de l’activité des étudiants, fichiers de traces, didactique des mathématiques MOTS CLÉS : Plate-forme d’enseignement, scénario a priori, analyse de l’activité des étudiants, fichiers de traces, didactique des mathématiques

ABSTRACT : Users of a learning platforms are usually required to log in, that provides a great deal of data. The general question studied here is: how to exploit this data to help the different actors involved? At first let us introduce the platform and the experiments we conducted. Then we use a didactic model to produce a qualitative analysis from the quantitative data collected. A simple exercise classification emerges from the construction of two indicators. It is consistent with the different experiments and relevant to the a priori didactic analysis. That allows us to organize results and perspectives according to the exercise classification and adapted to each role: designer, didactic researcher, and teacher KEYWORDS : Learning platforms, scenario a priori, analysis of students'activity, log files, didactic of mathematics

• 1. Introduction
• 2. Contexte d’apprentissage
• 3. Les expérimentations
• 4. Premiers résultats
• 5. Eléments pour une analyse didactique
• 6. Vers une typologie des exercices à partir des données traitées globales
• 7. Impact du scénario sur les exercices de la classe B
• 8. Conclusion
• BIBLIOGRAPHIE

1. Introduction

Les utilisateurs d’une plate-forme d’enseignement sont logués et leurs actions enregistrées dans de multiples fichiers. Ces fichiers fournissent un matériau très conséquent, facile à recueillir mais plus difficile à analyser. La question qui nous occupe ici est l’exploitation de ces fichiers pour obtenir des informations pertinentes permettant d’aider les différents acteurs dans leurs tâches respectives. Parmi les acteurs intervenant dans la production et l’utilisation de la plate-forme d’exercices, nous en repérons quatre. Le concepteur qui produit et adapte la plate forme, le didacticien qui étudie les relations entre enseignement et apprentissage et propose des ingénieries, l’enseignant qui vise un apprentissage pour un groupe d’étudiants et l’étudiant qui vise son propre apprentissage. La question générale est : dans une utilisation de la plate-forme, comment exploiter les fichiers de traces pour aider chacun dans sa propre tâche ? Cette question est vaste et nous n’en étudions que quelques aspects que nous allons spécifier.

Les travaux sur les analyses de traces sont récents, nombreux et leur ensemble est pour le moment désordonné. Nous retenons trois critères permettant de les décrire et de situer notre approche : le contexte, les objectifs et la méthode.

Le contexte concerne à la fois la plate-forme utilisée et le type d’enseignement. La plate-forme utilisée, que nous présentons plus loin, n’est pas une plate-forme d’enseignement à distance, mais plutôt une plate-forme d’exercices en ligne. Elle est utilisée en grande partie en présentiel et il n’y a pas dans nos dispositifs de tuteur en ligne. Notre but n'est pas la conception générale d'une plate-forme qui intègre une exploitation des fichiers de traces comme par exemple (Gueraud et al., 2004) et (Gueraud et Cagnat, 2004), mais l'exploitation de fichiers d'une plate-forme existante, très fortement utilisée, qui permet de recueillir de nombreuses données à tous les niveaux scolaires et sur quasiment tous les domaines des mathématiques. Ensuite, les traces que nous exploitons sont celles d’activités d'étudiants dans des résolutions d’exercices, par exemple le temps qu’un étudiant a passé sur un exercice, la note obtenue ou d’autres renseignements plus précis que nous expliciterons.

Les objectifs peuvent être ponctuels et répondre à une question de recherche : l’analyse de traces renseigne sur un ou plusieurs aspects de l’utilisation de la plate-forme, par exemple les contenus d’échanges explicites à travers un forum (Godinet, 2003), les aspects sociaux, communicationnels ou organisationnels (Dieumegard et al., 2004). Ils peuvent être aussi à portée plus générale en visant une utilisation régulière : plusieurs travaux proposent des outils pour faciliter le travail du tuteur ou de l’enseignant et lui permettre d’appréhender rapidement le travail de l’étudiant. Ainsi, CourseVis (Mazza et Dimitrova, 2004) est un outil permettant de rendre compte de l’activité des étudiants travaillant avec WebCT suivant trois aspects : sociabilité (participation aux forums), comportement (parcours dans le cours, les quiz, ..), aspects cognitifs (performance). D’autres outils, toujours à usage des enseignants ou tuteurs se focalisent sur les aspects didactiques. Dans le projet Lingot (Delozanne et al., 2003), les chercheurs construisent un logiciel d’aide au diagnostic à partir d’un modèle didactique de la compétence en algèbre élémentaire. Leur unité d’analyse relève de la micro compétence et le logiciel est construit dans le but du diagnostic pour le domaine précis de l’algèbre élémentaire au collège. Enfin, les chercheurs (Merceron et Yacef, 2004a), (Merceron et Yacef, 2004b) ont produit des outils visant à repérer des corrélations dans les protocoles d’activité sur des exercices de logique, c’est-à-dire des propriétés qui apparaissent souvent : si un étudiant commet par exemple tel type d’erreur logique, il est probable qu'il commette telle autre erreur. Ces renseignements permettent un retour sur l’analyse de tâche, la compréhension des processus d’apprentissage et peuvent aider à adapter l’ingénierie didactique.

Notre objectif n’est pas de construire un outil informatique permettant au tuteur une analyse rapide de traces. Nous cherchons plutôt par l’analyse de traces à obtenir des renseignements sur le fonctionnement didactique des étudiants. De telles recherches existent et leur problématique est proche de la nôtre : il s’agit de recueillir des données sur l’activité des étudiants afin d’en déduire des informations sur leurs apprentissages individuels, pour établir des diagnostics et des profils, ou des connaissances plus générales sur l’apprentissage plus global des mathématiques. Cependant, dans ces recherches, les logiciels sont souvent spécifiques d’un contenu et d’un niveau d’enseignement donné, parfois peu utilisés par les enseignants dits "ordinaires", ce qui permet des études fines mais met en œuvre des méthodologies très dépendantes de ces facteurs. Un groupe de chercheurs (Bouhineau et al., 2003) et (Bisson et al., 2003) a étudié des protocoles fournis par le logiciel APLUSIX. Ces protocoles sont plus précis que les nôtres car ils enregistrent chaque micro action de l’étudiant (clic de souris, frappe de clavier...). Les auteurs utilisent ces protocoles pour classer les exercices en fonction de la réussite des élèves et en inférer des variables didactiques (Brousseau, 1997) adéquates pour les analyses de tâches. Nous nous situons bien dans cette approche, cherchant à classifier ce que nous appellerons des adaptations de connaissances mathématiques (Robert, 1998). Ces chercheurs visent aussi à expliciter des stratégies de résolution d’équation et étudient la persistance de ces stratégies dans différents usages de l’EIAH, notamment s’il y a une rétroaction validant les procédures intermédiaires. Ils expliquent par ces exemples et leurs traitements comment l’analyse de protocoles peut permettre de rentrer "au cœur du fonctionnement des élèves".

La méthode utilisée diffère bien sûr suivant les objectifs visés. S’agissant de construire un outil générique, elle peut ou non reposer sur un modèle a priori de l’étudiant (Mazza, 2003). Dans tous les cas, une grande importance peut être accordée à la visualisation (Mazza et Dimitrova, 2004) qui permet d’appréhender un grand nombre de variables ; pour notre part, nous utilisons des représentations graphiques simples pour représenter des cohortes d’étudiants ainsi que des classes d’exercices.

Nous présentons d’abord la plate-forme d’exercices Wims, le contexte des expérimentations sur lesquelles nous nous appuyons et les premiers résultats très encourageants qui justifient la suite de ce travail. Il nous faut ensuite faire un détour pour expliquer les apports didactiques qui permettent de passer d’une information quantitative obtenue par les premiers résultats à une analyse qualitative. C’est ainsi que nous obtenons, par la construction de deux indices, une typologie des exercices de mathématiques qui met en évidence la cohérence et la complémentarité entre l’analyse didactique a priori des tâches et l’activité effective des étudiants. Ceci permet alors de souligner des caractéristiques propres à chaque catégorie d’exercices en lien avec l’apprentissage des étudiants. Nous étudions ensuite, grâce aux outils construits, l’impact du scénario sur l’apprentissage dans les expérimentations analysées. La conclusion reprend, pour les différents acteurs, les résultats obtenus et les perspectives offertes par cette analyse didactique des fichiers de traces.

2. Contexte d’apprentissage

2.1. Présentation générale du serveur Wims

Le serveur Wims (http://wims.unice.fr/wims) est un serveur interactif d'exercices, développé à l’initiative individuelle de XIAO Gang et d’usage libre. Le site originel se situe à l’Université de Nice. Plusieurs sites miroirs existent en France dont celui de l'Université d'Orsay ; mais aussi à l'étranger (Chine, Etats-Unis, Espagne, Italie, Pays-Bas) traduits dans 6 langues différentes. Les ressources proposées sont essentiellement mathématiques mais commencent à concerner la physique, la chimie, la géographie et la grammaire. Le niveau visé est aussi bien l'enseignement supérieur que l'enseignement secondaire. Une communauté d’utilisateurs et de développeurs se constitue depuis 1998 et, par exemple, le nombre de classes ou groupes de classes dépasse largement la centaine sur le seul site miroir de l’Université d’Orsay. On consultera (Ramage et Perrin, 2004) et (Xiao, 2000) pour des statistiques plus détaillées. Ceci justifie pleinement que l’on s’intéresse à cette plate-forme très utilisée, même si les traces qu’elle nous permet de recueillir sont totalement brutes.

Le serveur Wims utilise une interface avec des logiciels libres de calcul et de dessin (pari, maxima, gap, octave, mupad). Il bénéficie ainsi de l'évolution de ces logiciels et de leur augmentation de puissance. Voici la page d’accueil du serveur Wims de l’Université d’Orsay.

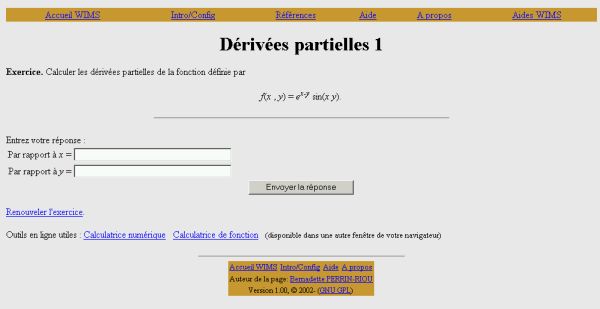
Figure 1 : Page d’accueil du serveur Wims d’Orsay

Le serveur s’adresse aussi bien aux enseignants qu’aux étudiants. Les ressources sont de trois types : des ressources pédagogiques interactives sous forme de cours et d’exercices, des outils de calculs ou de graphismes et enfin des classes virtuelles. C’est cette dernière fonctionnalité qui nous intéresse et que nous allons détailler dans les paragraphes suivants. Le serveur Wims se rapproche dans cette utilisation d’une plate-forme pédagogique. Elle s’adresse aux enseignants qui peuvent inscrire leurs élèves dans leur classe virtuelle et les faire travailler sur un choix de ressources pédagogiques Wims. Chaque étudiant possède alors un identifiant et un mot de passe ; toutes les traces de son activité sur le serveur Wims sont enregistrées.

2.2. Un exercice Wims

Une spécificité de Wims est que les exercices proposés aux étudiants sont programmés et que les paramètres des énoncés sont à variation aléatoire. C'est-à-dire qu’un étudiant peut refaire plusieurs fois le même exercice sans que ce soit exactement le même énoncé ou encore qu’en classe, des étudiants côte à côte ne travaillent pas sur le même énoncé d’un exercice. Voici un exemple d’exercice :

Figure 2 : Exercice Dérivées partielles 1

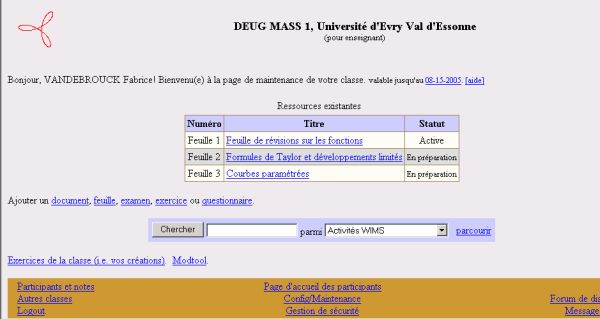
Lorsque l’étudiant relance l’exercice, il se voit proposer une autre fonction de 2 variables établie aléatoirement par Wims à partir de valeurs numériques aléatoires et d’un panel de fonctions classiques prédéfinies par le concepteur.

Les réponses attendues sont en général des valeurs numériques, des expressions algébriques ou des réponses à des QCM. Elles sont analysées par les logiciels de calcul et Wims attribue un score, nombre de points variant de 0 à 10, à chaque fois qu’un exercice est exécuté. Wims donne en général la bonne réponse à l’exercice exécuté mais jamais la façon de l’obtenir. Certains exercices proposent, parmi les outils Wims, une aide que les étudiants peuvent activer comme ils le souhaitent.

2.3. Une feuille de TD Wims

Les enseignants proposent des feuilles de travaux dirigés (TD-Wims) qu’ils élaborent en choisissant et en organisant des exercices Wims. Ils peuvent alors recueillir la moyenne de chacun de leurs étudiants pour chaque exercice, pour chaque feuille de TD-Wims ou pour l’ensemble des feuilles de TD-Wims.

Figure 3 : Espace de travail personnel d’un étudiant

Les étudiants ont la liberté de faire les exercices dans l’ordre qu’ils veulent. Ils peuvent également choisir d’activer ou de suspendre l’enregistrement de leurs scores. C’est-à-dire qu’ils peuvent s’entraîner "à blanc" sur chacun des exercices des feuilles de TD-Wims. Lorsqu'ils se sentent prêts, ils peuvent alors activer l’enregistrement de leurs scores pour que les notes obtenues comptent dans leur moyenne.

Figure 4 : Une feuille de travail

3. Les expérimentations

3.1. Organisation générale

Nous nous appuyons sur deux familles d'expérimentations qui se déroulent sur le long terme depuis l’année universitaire 2002/2003 à l’Université d’Evry (expérimentations EVRY 2003 et EVRY 2004 en DEUG MASS première année) et à l’Université d’Orsay (expérimentations ORSAY 2003, ORSAY 2004 et ORSAY 2005 en DEUG Sciences de la Matière deuxième année). Les contenus d’enseignements expérimentés sont, à EVRY, les fonctions numériques et, à ORSAY, les fonctions de deux variables réelles (l’exercice Dérivées partielles 1 est extrait des expérimentations ORSAY). Les étudiants sont une vingtaine dans chacune des expérimentations, seuls devant leur machine sauf pour l’expérimentation EVRY 2003 où ils sont 36 et en binômes. Il s’agit d’étudiants ordinaires qui constituent des groupes de TD hétérogènes. Dans toutes ces expérimentations, ils travaillent en présence de leur enseignant dans le cadre de séances de TD-Wims dans les universités. Ils ont aussi la possibilité de travailler en salle libre service ou chez eux, le serveur Wims étant en ligne. Dans toutes les expérimentations, les notes fournies par le logiciel Wims interviennent dans le contrôle continu pour la validation des modules de mathématiques ce qui constitue un élément fort du contrat didactique (Brousseau, 1997) qui les lie à l’institution. Les étudiants n’ont cependant pas la possibilité d’activer l’enregistrement de leurs notes lorsqu’ils sont en libre service ou chez eux ; ils ne peuvent que s’entraîner "à blanc". Enfin, ils ne savent pas que les traces de toute leur activité font l’objet d’une analyse didactique afin que ne soit pas altérée par cette information leur activité naturelle sur le logiciel Wims.

3.2. Données recueillies

Les données recueillies sont de deux types : des données brutes individuelles sur le parcours de chaque étudiant fournies par le serveur Wims (journaux de traces) et des données traitées par étudiant et par exercice, obtenues en important les données brutes dans des fichiers Excel. Voyons successivement ces deux types de données.

3.2.1. Les journaux de traces de l’activité des étudiants

Nous donnons un extrait d’un journal de traces de l’activité de l’un des étudiants de l’expérimentation EVRY 2004. L’étudiant travaille ici le 10 mars 2004, de 13h43 à 14h04 sur l’exercice 2 de la deuxième feuille de TD-Wims.

Tableau 1 : Extrait d’un journal de traces de l’activité d’un étudiant

Dans la colonne Etat, la mention new (ou renew) signifie que l’étudiant lance l’exercice. La mention score signifie qu’il soumet une réponse au logiciel. La note donnée par Wims est alors inscrite dans la colonne Score. L’état d’enregistrement noscore signifie que l’étudiant n’a pas activé l’enregistrement et donc qu’il s’entraîne sur l’exercice. Ainsi, à 14h03 (avant dernière ligne), l’étudiant active l’enregistrement des scores, relance l’exercice 2 sur lequel il s’entraînait depuis 13h43 et obtient la note de 10, seule note qui va contribuer à sa moyenne comptabilisée sur l’exercice.

3.2.2. Données traitées

Pour chaque étudiant et chaque exercice, nous obtenons dans un premier temps les données traitées suivantes :

Tableau 2 : Données traitées pour un étudiant sur un exercice

Il s’agit des données traitées de l’un des 21 étudiants de l’expérimentation ORSAY 2003 sur l’exercice Dérivées partielles 1. La durée de la première rencontre est le temps passé par l’étudiant pour soumettre son premier résultat sur l’exercice (temps entre le premier new et le premier score). Le temps pour avoir la note maximale de 10 sur 10 est le temps entre le premier new et le premier score 10 s’il existe. Ensuite viennent le nombre de new, c’est-à-dire le nombre de fois où l’exercice est exécuté et le nombre de score, toujours inférieur, qui est le nombre de fois où une réponse est proposée par l’étudiant. Enfin viennent des informations sur le nombre de points de l’étudiant à l’exercice et les moyennes. Dans ces données traitées, nous ne distinguons pas les points que l’étudiant a enregistrés pour sa moyenne comptée de ceux qu’il a obtenu "à blanc". Nous recueillons également, sous la même forme, la date et l’heure du premier new, du premier score, du premier score enregistré par l’étudiant, du premier 10 sur 10, du premier 10 sur 10 enregistré par l’étudiant et enfin la date et l’heure du dernier score enregistré.

Tableau 3 : Données traitées pour un étudiant sur un exercice (suite)

Ces données nous permettent de retracer le parcours de chacun des étudiants et surtout de retrouver l’ordre dans lequel ils abordent et réussissent les exercices. Le recueil dans chaque expérimentation des données traitées pour chaque étudiant et chaque exercice permet enfin d’obtenir des données traitées globales relatives à chaque exercice :

Tableau 4 : Données traitées globales pour un exercice

Il s’agit des données traitées globales pour l’expérimentation d’ORSAY 2003 sur l’exercice Dérivées partielles 1. Les étudiants, lorsqu’ils travaillent sur cet exercice, sont en cours de semestre. Ils sont donc habitués au travail sur machine et au logiciel. Les données traitées globales permettent de recueillir dans la troisième colonne du tableau 4 des moyennes et des totaux pour chaque exercice à partir des données individuelles des étudiants ayant travaillé dans la classe virtuelle. La deuxième colonne du tableau 4 donne le nombre d’étudiants sur lequel est calculé le total ou la moyenne de la ligne correspondante. Dans cet exemple, 21 étudiants ont travaillé l’exercice mais seulement 16 d’entre eux ont obtenu plus de 3 notes. La cinquième ligne est le nombre de new relevés pour l’ensemble des 21 étudiants de l’expérimentation. Dans cet exemple, l’exercice a été exécuté 145 fois, soit 6,9 fois en moyenne par étudiant. La sixième ligne est le nombre total de score relevés. Sur les 145 exécutions, seules 117 ont abouti à la soumission d’un résultat. La septième ligne est le total des points recueillis.

4. Premiers résultats

Une première lecture des résultats conduit aux conclusions suivantes : les étudiants travaillent beaucoup sur le serveur Wims, cependant tous les étudiants ne travaillent pas de la même manière et tous les exercices ne sont pas travaillés non plus de la même façon.

4.1. Une forte activité des étudiants

Ce résultat consensuel, déjà obtenu par exemple par des analyses d'entretiens par (Ruthven et Henessy, 2002), est clairement illustré et objectivé par les durées de connexion ci-dessous. Dans l’expérimentation EVRY 2003, les 36 étudiants ont travaillé pendant 8 séances d’une heure trente, soit 11 heures de connexion théorique pendant des séances de TD à l'Université (les étudiants travaillaient en binôme pendant ces séances). Dans l’expérimentation ORSAY 2003, les 21 étudiants ont travaillé pendant 9 séances, soit 7 heures de connexion théorique (les étudiants étaient ici seuls sur leurs machines). Cependant les durées totales de connexion sur le serveur Wims dépassent, pour 80% des étudiants, les durées de connexions théoriques en séances :

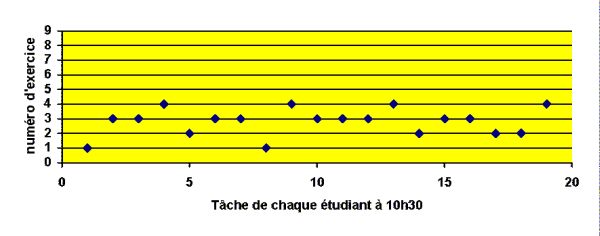
Tableau 5 : Durées totales de connexion des étudiants

Ces durées totales ont été recueillies en sommant les durées totales de connexion des étudiants sur chacun des exercices des feuilles de TD-Wims proposées. Ce tableau signifie que, non seulement les étudiants assistent vraisemblablement à toutes les séances de TD, mais encore qu’ils travaillent personnellement chez eux ou en libre-service ce qui n’est pas toujours le cas dans les dispositifs d’enseignement classique où l’absentéisme est souvent important et le travail personnel faible. Si nous admettons qu’un intermédiaire important des apprentissages est constitué par les activités propres des élèves sur des tâches mathématiques, nous retenons ce résultat comme important pour alimenter l’hypothèse selon laquelle le travail sur logiciel peut favoriser leur apprentissage.

4.2. Une activité différente suivant les étudiants

4.2.1. Au même moment les étudiants travaillent sur des exercices différents

C’est là aussi un atout des TICE très souvent mis en avant par les utilisateurs : le travail sur machine permet à chacun d’avancer à son rythme en s’affranchissant de la pesanteur du groupe. La figure suivante, obtenue à partir des journaux de traces des étudiants d’ORSAY illustre ce résultat :

Figure 5 : Tâche des étudiants sur une feuille d’exercices à un instant donné

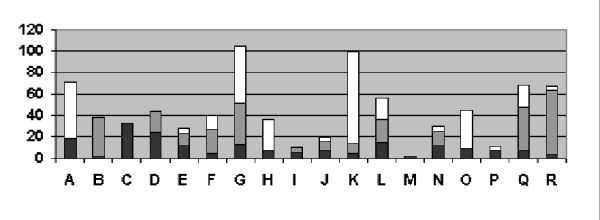
Dans ce graphique, chaque point représente l'un des 19 étudiants de la classe d’ORSAY 2003 (il y avait deux absents ce jour-là) et l’exercice sur lequel il travaille à 10h30. La feuille de TD-Wims Fonctions de plusieurs variables comporte 9 exercices (en ordonnée). On constate par exemple que l’étudiant 1 cherche l’exercice 1 Dérivées partielles 1 tandis que les étudiants 2 et 3 travaillent sur l’exercice 3. Il apparaît clairement que, même si les étudiants travaillent sur la même feuille de TD, ils sont maîtres de leur progression. Ceci n’est pas le cas en séance de TD classique où les corrections collectives notamment, imposent très souvent une marche commune du groupe.

4.2.2. Les étudiants ont des formes de travail différentes sur les exercices

La figure suivante complète celle du paragraphe précédent. Il s’agit des 18 binômes de l’expérimentation EVRY 2003 travaillant sur l’un des exercices de l’expérimentation :

Figure 6 : Forme de travail des étudiants sur un exercice

En ordonnée, les données représentent des durées de travail en minutes. Pour chaque binôme, la zone noire représente la durée de la première rencontre avec l’exercice (temps entre le premier new et le premier score). La zone grise représente le temps supplémentaire nécessaire au binôme pour obtenir la note de 10. Cette zone peut-être réduite à zéro si le binôme a obtenu 10 dès la première rencontre ou inexistante si le binôme n’obtient jamais 10. La zone blanche représente enfin la durée de travail supplémentaire, après avoir obtenu la note maximale de 10. Elle peut être aussi nulle si le binôme n'éprouve pas le besoin de continuer à travailler après son premier 10. Ce graphique, encore plus que le précédent, met en évidence la grande liberté d’action des étudiants sur chacun des exercices : ils travaillent non seulement au moment où ils veulent mais pendant le temps qu’ils souhaitent et selon l’organisation qui leur convient.

Il est tentant alors de faire le lien avec le concept d’autonomie et les questions qu’il pose (Linard, 2003). De quelle autonomie s’agit-il ? Par exemple, les écarts mis en évidence par les schémas ci-dessus illustrent-ils une différence de rapidité dans la résolution des exercices ou de stratégie dans le travail de la feuille de TD, certains étudiants décidant de refaire plusieurs fois les mêmes exercices ou au contraire de passer certains exercices ? Dans quelle mesure les étudiants ont-ils conscience de ces libertés permises par le scénario d’usage. Comment gèrent-ils ces libertés ? Ces pistes nous paraissent intéressantes à poursuivre mais nous nous concentrons maintenant sur une approche plus didactique.

4.2.3. Les étudiants ont des activités différentes suivant les exercices

Certains exercices correspondent manifestement à un saut de difficulté. L’analyse a priori des tâches en jeu peut permettre de distinguer de tels exercices. L’étude des journaux de traces a posteriori peut conforter cette analyse mais aussi la dépasser et rendre les deux points de vues complémentaires comme nous allons le montrer plus loin. La figure suivante montre l’avancement du travail des étudiants sur la feuille Fonctions de plusieurs variables pendant l’expérimentation ORSAY 2003 :

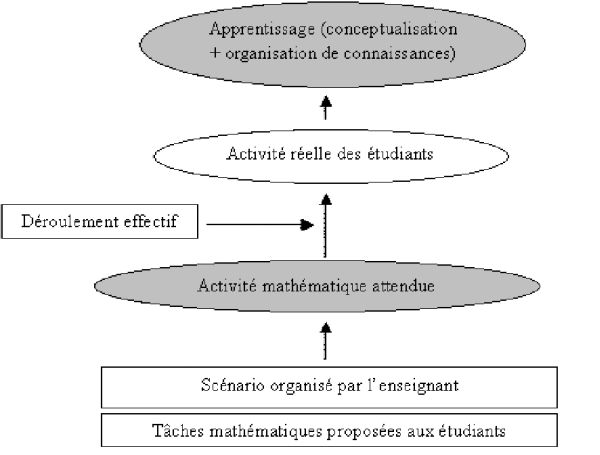
Figure 7 : Rythme des étudiants sur une feuille d’exercices (2)

Cette figure montre que l’étudiant 1 travaille toujours sur l’exercice 1 à 10h30 comme à 10h45, tandis que l’étudiant 2 est passé de l’exercice 3 à l’exercice 6. On constate que l’exercice 4 agit comme une barrière. La majorité des étudiants travaillent sur cet exercice à 10h45. Les étudiants 4, 9, 13 et 19 qui travaillaient l’exercice 4 à 10h30 sont en fait toujours dessus à l’issue du quart d’heure considéré. Nous ne savons pas en quoi ces phénomènes participent ou non aux apprentissages des étudiants. Nous introduisons maintenant des éléments de didactique pour aller plus en profondeur dans notre recherche.

5. Eléments pour une analyse didactique

5.1. Schéma théorique 

Nous représentons ce qui se joue en séance Wims par le schéma suivant qui se lit de bas en haut :

Figure 8 : Schéma théorique didactique

Dans ce schéma, les ovales grisées représentent les informations sur les étudiants que l’on ne peut inférer qu’à partir d’analyses didactiques. Tel est l’apprentissage des étudiants, lié à la conceptualisation et à l’organisation de connaissances mathématiques (Robert, 1998). Pour permettre cet apprentissage, l’enseignant propose aux étudiants un certain nombre de tâches mathématiques par l’intermédiaire d’un scénario. Nous représentons tâches et scénarios par des rectangles blancs signifiant que l’on a un accès réel à ces données. Dans nos expérimentations, les tâches sont associées aux exercices Wims et les scénarios correspondent aux différents exercices dans l’ordre proposé par l’enseignant dans ses feuilles Wims. Idéalement, la réalisation de chacune des tâches au sein du scénario engendre une activité mathématique. Cette activité concerne des étudiants génériques, qui  "jouent le jeu". On peut donc parler d’activité mathématique attendue (ou potentielle) des étudiants. C’est bien l’étude didactique a priori des tâches et du scénario qui permet d’inférer cette activité. Les flèches du schéma théorique représentent ces inférences. Au delà du simple contenu de l’exercice, nous retenons pour cette analyse les types de connaissances mises en jeu et la nature des mises en fonctionnement de ces connaissances (Robert et Rogalski, 2002). Ces mises en fonctionnement sont-elles des applications plus ou moins immédiates de connaissances ou bien y a-t-il au contraire des adaptations à apporter : reconnaître une ou des connaissances avant de les appliquer, introduire des étapes, des intermédiaires, travailler dans plusieurs cadres mathématiques (Douady, 1986), travailler sur plusieurs registres de représentations (Duval, 1993)...). Notre hypothèse didactique est qu’une activité "riche", générée par des tâches mathématiques dépassant les applications immédiates de connaissance et nécessitant des adaptations va favoriser l’apprentissage de mathématiques. Un des enjeux de l’étude des traces en didactique des mathématiques est, pour une connaissance ou un type de connaissances donné, de classifier ces adaptations selon la difficulté des étudiants à les surmonter.

Dans la réalité, le déroulement effectif de la séance, notamment tous les échanges entre étudiants, les aides de l’enseignant, le choix fait par chaque étudiant de l’ordre des exercices qu’il travaille modifie l’activité attendue des étudiants. A nouveau, le déroulement effectif de la séance est représenté par un rectangle blanc dans notre schéma théorique car il est possible d’avoir accès à cette donnée. Chacun des étudiants produit alors une activité réelle. Nous la représentons par une forme ovale blanche car une partie de cette activité peut être décrite par des observations directes ou ici par l’étude des journaux de traces. En complément, une partie de l’activité réelle est aussi inférée à partir de l’activité attendue et du déroulement effectif.

5.2. Illustration sur un exemple

Revenons au cas de l’expérimentation d’Orsay 2003 présentée plus haut où l’exercice 4 est un exercice barrière et étudions successivement les activités attendues et ce que nous apprennent les données traitées sur l’activité réelle des étudiants. Pour distinguer, comme dans notre schéma théorique, l’influence du scénario sur l’activité attendue des étudiants, nous détaillons l’activité attendue sur l’exercice 4 isolé puis l’activité attendue compte tenu du scénario.

5.2.1. Activité attendue sur l’exercice isolé

Voici précisément l'énoncé de l’exercice 4 Composition II Dérivées partielles. Il consiste en un calcul d’une dérivée partielle seconde d’une fonction composée de 2 variables avec l’une des deux fonctions implicite :

Figure 9 : Exercice Composition II Dérivées partielles

L’exercice 4 est constitué de plusieurs applications non indépendantes (imbriquées) de connaissances sur les dérivées partielles et sur les compositions de fonctions. L’étudiant doit appliquer la formule de dérivation seconde d’une fonction composée à deux variables. Ceci étant, il peut simplifier sa tâche et faire un calcul formel directement en s’aidant du format de réponse attendu. Quelle que soit la méthode retenue par l’étudiant, cet exercice reste une suite d’applications de connaissances sans adaptations véritables à apporter. Nous le qualifions d’exercice technique. Cependant, il s’agit d’un exercice très long et les applications sont non indépendantes ce qui contribue à la difficulté.

5.2.2. Activité attendue compte tenu du scénario

L’étude du scénario est la prise en compte du contexte et notamment des trois exercices qui précèdent l’exercice 4 Composition II Dérivées partielles. L’analyse de tâches amène à les qualifier également d’exercices techniques, c'est-à-dire qu’il s’agit d’exercices d’applications de connaissances. Il n’y a pas véritablement d’adaptations de ces connaissances à mettre en œuvre mais l’analyse comparative de ces exercices permet de dire que les applications sont a priori de plus en plus complexes :

- Exercice 1 : il s’agit de l’exercice Dérivées partielles 1 rencontré dans la partie 2 ; c’est-à-dire un exercice technique avec deux applications immédiates indépendantes des règles de dérivations (dérivée partielles par rapport à la variable x puis dérivée partielle par rapport à la variable y).

- Exercice 2 : Dérivées partielles 2. Il s’agit ici de calculer une dérivée partielle seconde, c’est-à-dire d’enchaîner deux fois la même application immédiate. La complexité de la fonction est la même que dans l’exercice 1 mais les deux applications sont non indépendantes, ce qui augmente la difficulté.

- Exercice 3 : Composition I Dérivées partielles. Il s’agit toujours d’un exercice technique mais, comme pour l’exercice 4, deux connaissances sont en jeu : les étudiants doivent d’une part appliquer de façon immédiate la formule de dérivation des fonctions composées et d’autre part calculer deux dérivées partielles premières indépendantes. Le format de réponse constitue cependant une aide pour l’application de la formule de dérivation composée.

L’exercice 4 apparaît donc comme le prolongement de l’exercice 3. Pour cet exercice 4, les étudiants vont très certainement calculer d’abord la dérivée partielle première de la fonction composée proposée (ce qui correspond exactement à la tâche de l’exercice 3) puis la dériver à nouveau pour retrouver la formule donnée dans l'analyse de tâches de l’exercice 4. L’exercice 4 est donc plus long que les 3 précédents, ce qui permet de comprendre a priori le rôle barrière qu'il joue et que l’on a clairement constaté à la figure 7.

5.2.3. Activité réelle des étudiants sur les 4 exercices

Nous n’avons pas dans ces expérimentations les détails du déroulement effectif des séances, notamment les interventions orales de l’enseignant. Cependant, la prise en compte des données traitées globales permet d'obtenir des informations sur l'activité réelle des étudiants en atténuant les effets de telles ou telles aides apportées ponctuellement à certains étudiants et pas à d'autres. Voici les données traitées globales pour les 19 étudiants d’ORSAY 2003 ayant travaillé sur les 4 exercices (la première et la cinquième colonne sur fond blanc donnent les nombres d’étudiants) :

Tableau 6 : Données traitées globales sur les 4 exercices d’ORSAY 2003

On constate que l’exercice 4 est cherché beaucoup plus longtemps que les trois autres, pour un nombre total de points et une moyenne qui sont moindres. Les temps moyens pour proposer une réponse et pour obtenir la note maximale de 10/10 sont beaucoup plus longs tandis que seulement 16 et 11 étudiants ont réussi à fournir une réponse ou à atteindre 10/10. Ceci est bien cohérent avec l’analyse de la tâche et l’activité attendue. Les données traitées globales permettent cependant d'affiner les analyses a priori puisqu'elles mettent en évidence l'apprentissage des étudiants sur les 3 premiers exercices. Tout d’abord les 19 étudiants font les 4 exercices dans l’ordre de la feuille. Ils réussissent tous les trois premiers exercices. Le temps moyen de travail par étudiant est en baisse pour ces trois premiers exercices tandis que la moyenne des notes par étudiant est en hausse. Les étudiants cherchent donc de moins en moins longtemps et pourtant obtiennent un score de plus en plus élevé. Ce dernier point n’était pas révélé par l’analyse a priori de l’activité mathématique attendue.

6. Vers une typologie des exercices à partir des données traitées globales

Pour un scénario donné, en particulier pour une feuille de TD-Wims donnée, nous essayons de catégoriser les exercices à partir des activités réelles des étudiants. Cette catégorisation est donc a priori relative car elle est dépendante du logiciel Wims, de la séquence, des contenus étudiés et aussi des élèves de chaque groupe. Toutefois, la méthodologie et les résultats relèvent d’une généralité que nous expliquerons.

6.1. Synthèse des données traitées globales : indice de difficulté et rendement

Nous définissons, pour chaque exercice, deux indicateurs : l’indice de difficulté de l’exercice et le rendement de l’exercice. L’indice de difficulté est le rapport entre le nombre de fois où l’exercice est cherché (nombre total de new) et le nombre de fois où un étudiant soumet un résultat, c'est-à-dire se voit attribué un score (nombre total de score). Nous estimons que ce rapport permet de prendre en compte l’activité des étudiants en dépassant le simple recueil des scores moyens obtenus par les étudiants. En effet, plus cet indice est proche de 1, plus l’exercice a été traité (pas forcément de manière juste) par les étudiants. En revanche, plus cet indice s’éloigne de 1, plus les étudiants ont "séché" sur l’exercice au point de ne pas pouvoir soumettre de réponse. Le rendement est le rapport entre le nombre de points total obtenu par les étudiants et le temps total de travail des étudiants sur l’exercice. Ces deux indicateurs permettent de prendre en compte, de façon synthétique, les principales données traitées globales recueillies sur chacun des exercices et vont au delà du simple recueil de la moyenne de la classe à l’exercice. Ils semblent indépendants car ils utilisent des données différentes ; cependant il se peut que ces données soient corrélées. Ils sont également indépendant du contenu mathématique et en ce sens plus généraux que ceux définis par exemple par (Merceron et Yacef, 2004b) pour les contenus de logique et permettent une classification des exercices mathématiques en trois classes dont il nous semble qu’elle peut s’exporter à d’autres plates-formes d’exercices.

Nous présentons dans le tableau ci-dessous, pour chaque exercice de la feuille de TD-Wims Fonctions de plusieurs variables de l’expérimentation ORSAY 2003, un résumé de l’analyse de tâches a priori et les valeurs calculées a posteriori des indices de difficulté et des rendements.

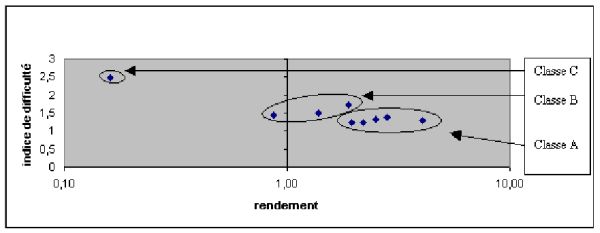
Tableau 7 : Analyse de la feuille WIMS dans l’expérimentation ORSAY 2003

Les deux dernières colonnes de ce tableau (indicateurs de l’activité réelle des étudiants) se synthétisent en un graphique qui permet de distinguer 3 classes d’exercices cohérentes avec les analyses de tâches a priori (activité attendue des étudiants dans la deuxième colonne) :

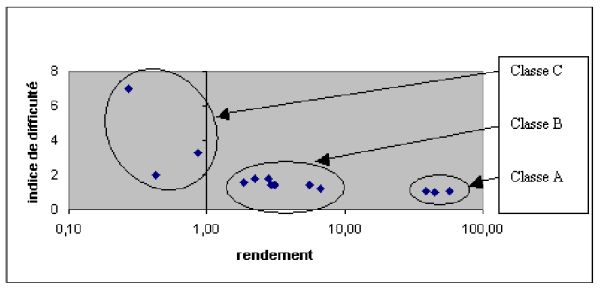
Figure 10 : Profil des exercices dans l’expérimentation ORSAY 2003

- Classe A : Les exercices simples (exercices 1, 2, 3, 7 et 9) sont des exercices situés dans la zone à la fois la plus à droite et la plus basse. Ce sont des exercices techniques d’applications essentiellement immédiates et indépendantes de connaissances.

- Classe C : Les exercices difficiles (exercice 8) mettent en jeu de nombreuses adaptations de connaissances (on parle aussi de tâches complexes (Robert, 1998)). Il est situé dans la zone gauche du graphique (on distinguera lorsqu’on étudiera plus finement des exercices de cette classe les zones de gauche en haut et de gauche en bas).

- Classe B : Les exercices intermédiaires (exercice 4, 5, 6) sont situés dans une zone médiane. Les tâches en jeu dans ces exercices sont variées, au-delà des applications immédiates ou indépendantes de connaissances mais sans que l’on puisse pour le moment mieux préciser la typologie et mieux classifier les adaptations des connaissances.

Comme dans toute typologie, les frontières sont arbitraires. Cependant, nous trouvons intéressant la concordance et la complémentarité entre l’analyse de tâche a priori et les données traitées globales a posteriori. En effet, dans toutes nos expérimentations, le graphique est établi à partir de l’activité réelle des étudiants et permet toujours de repérer a posteriori trois classes d’exercices. C’est seulement pour interpréter ces classes que nous nous appuyons sur l’analyse didactique a priori des exercices et que nous constatons la cohérence que nous allons détailler plus loin. Cependant, la dépendance au scénario se traduit par le fait que l’on ne puisse pas isoler un exercice du graphique et s’attendre à avoir exactement les mêmes caractéristiques en terme d’indice de difficulté et de rendement pour cet exercice dans un contexte différent (même avec un scénario identique). C’est seulement la classe d’un exercice qui est un invariant compte tenu d’un scénario. Il est donc important de caractériser les exercices au sein d’une feuille de TD-Wims pour voir apparaître leur appartenance à telle ou telle classe d’exercice. Nous appliquons maintenant la même méthodologie à l’expérimentation EVRY 2004. Bien que sur un contenu mathématique différent de l’expérimentation ORSAY 2003, nous obtenons un graphique
similaire :

Figure 11 : Profil des exercices de l’expérimentation EVRY 2004

Les trois classes d’exercices apparaissent encore plus nettement dans cette expérimentation. Notons que les deux indices ne sont a posteriori pas indépendants puisqu’on ne trouve pas d’exercices dans la zone du haut à droite. Ceci traduirait une dérive majeure du système. En effet, ces exercices seraient rentables, donc ils rapporteraient des points en très peu de temps, et pourtant les énoncés seraient perçus comme difficiles par les étudiants (indice de difficulté élevé). Plutôt que de faire un résumé systématique de l’analyse des tâches de chacun des exercices comme pour ORSAY 2003 dans le tableau précédent, nous proposons de fournir un exemple de chacune des catégories. Nous étudions en effet plus finement maintenant, pour chaque classe d’exercice, les traces individuelles des étudiants. Ces catégories nous permettent de moduler les observations sur l’activité individuelle des étudiants en fonction de la classe de l’exercice.

6.3. Etude de chacune des trois classes d’exercices

6.3.1. Les exercices de la classe A, à portée limitée, pas si immédiats, parfois trop travaillés

L’étude des données traitées montre que ces exercices ne sont pas totalement immédiats : il faut beaucoup de temps aux étudiants pour les résoudre correctement lors de la première rencontre et pour avoir la note maximale de 10. L’exercice dérivées partielles 1 dans l’expérimentation ORSAY 2003 est en classe A. Voici les données traitées globales sur cet exercice :

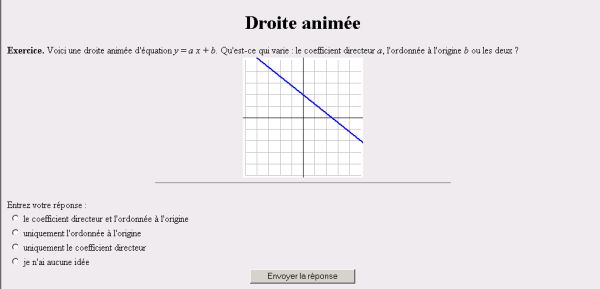
Tableau 8 : Extrait de données traitées globales sur l’exercice Dérivées partielles 1

Le temps moyen à la première rencontre est de 7.45 min et le temps moyen pour que les étudiants obtiennent la note maximale de 10 est 17.24 min en moyenne, ce qui est relativement long compte tenu de l’analyse des tâches que l’on a faite de cet exercice (deux calculs de dérivées partielles premières indépendants, soit deux applications immédiates indépendantes).

Nous donnons l’exemple de l’un des trois exercices de la classe A dans l’expérimentation EVRY 2004 : le graphe de la fonction affine est animé, la droite pivote soit autour de son intersection avec l’axe des ordonnées, soit autour d’un point quelconque, soit se déplace par translation.

Figure 12 : Exercice Droite animée de l’expérimentation EVRY 2004

Pour des étudiants de première année d’université, cet exercice ne met en jeu que des connaissances très anciennes de la classe de troisième sur les droites affines. L’adaptation de connaissance due au changement de cadre (les données sont dans le cadre graphique alors que la réponse est demandée dans le cadre algébrique) ne peut pas être retenue et il s’agit donc d’un exercice technique d’application immédiate de connaissances sur les droites affines. Les données traitées pour cet exercice montrent à nouveau que les temps moyens à la première rencontre et pour obtenir la note maximale de 10 sont relativement longs.

Tableau 9 : Extrait de données traitées globales sur l’exercice Droite animée

Sur ces exercices, l’apprentissage est cependant visible : la quasi-totalité des étudiants les réussit, la moyenne générale des étudiants est bonne et la moyenne des trois dernières notes est toujours sensiblement supérieure à celle des trois premières. Une étude encore plus détaillée des fichiers de traces montrerait même que l’augmentation est linéaire jusqu’à la note maximale de 10.

La portée de ces exercices est clairement limitée pour un apprentissage des mathématiques au niveau du premier cycle universitaire. Ceci étant, le travail sur ces exercices faciles semble nécessaire aux étudiants pour assurer des bases solides. L’étude des données traitées globales montre que le temps de travail total des étudiants sur ces exercices faciles est élevé : plus de 9 heures par exemple sur l’exercice Dérivées partielles 1 de l’expérimentation ORSAY 2003, soit plus de 25mn par étudiant alors qu’il ne s’agit que de calculer des dérivées premières de fonctions de 2 variables réelles. Comme ces exercices techniques de classe A sont souvent considérés comme fastidieux par l’enseignant, ils ne sont pas toujours traités en TD classiques et quand ils le sont, le rythme individuel des étudiants est plus difficilement respecté. Ceci justifie l’usage de la base d’exercices pour le travail sur ces exercices.

L’étude montre aussi que certains étudiants refont sans cesse ces exercices simples : il semble qu’ils veuillent absolument approcher la moyenne de 10 sur 10, quitte à refaire sans arrêt les mêmes tâches. Il y a parfois de longues séries de scores 10 dans les journaux de traces. Voici par exemple des données traitées pour cinq des étudiants de l’expérimentation EVRY 2004 sur l’exercice Droite animée : leur total des notes est pour tous les cinq supérieur à 200.

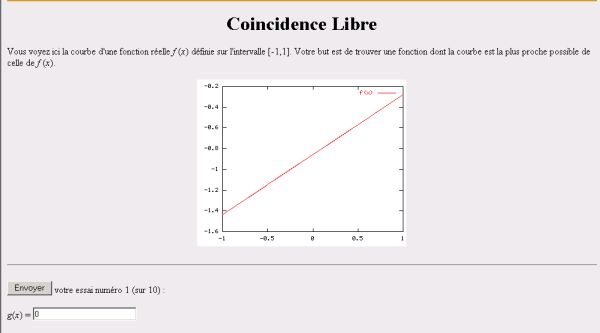
Tableau 10 : Extrait de données traitées pour 5 étudiants sur l’exercice Droite animée

Il y a là un effet de contrat manifeste puisque ces étudiants, dans une logique de réussite à la feuille de TD-Wims, préfèrent améliorer leur moyenne sur cet exercice facile plutôt que d’affronter les exercices plus difficiles. Ces dérives suggèrent l’idée, pour le concepteur, de limiter l’accès aux exercices de classe A après une série de 5 scores 10, voire d’accorder alors la note maximale de 10 sur 10 pour ne pas frustrer les étudiants stoppés.

6.3.2. Les exercices de la classe C, difficiles mais qui ne découragent pas les étudiants

Dans l’expérimentation ORSAY 2003, il n’y a qu’un seul exercice difficile : Pente et gradient dont l’analyse de tâche est faite succinctement dans le tableau 7. Il s’agit d’un exercice difficile avec une tâche de modélisation d’une situation géographique. Les connaissances sur le gradient doivent être adaptées pour résoudre l’exercice, en particulier le gradient doit être utilisé comme un outil de résolution et non pas comme un objet mathématique (Douady, 1986). Il y a ensuite plusieurs étapes de calculs.

Dans l’expérimentation EVRY 2004, nous considérons deux exercices de la classe C, l’un dont l’indice de difficulté est faible (Coïncidence libre version affine) et l’autre dont l’indice de difficulté est le plus élevé de tous les exercices de l’expérimentation (Coïncidence libre version courbe). Il s’agit là encore de deux exercices difficiles qui mettent en fonctionnement des connaissances sur les droites affines et sur les équations de degré 2. Il ne s’agit pas d’applications immédiates de ces connaissances. Outre le nouveau changement de cadre, les étudiants doivent adapter leurs connaissances, reconnaître la forme affine et la forme second degré, puis choisir parmi plusieurs méthodes possibles de résolution. Voici un énoncé de l’exercice Coïncidence libre version affine. Un énoncé de l’exercice Coïncidence libre version courbe est similaire, le graphique représentant alors une courbe du second degré.

Figure 13 : Exercice Coïncidence Libre version affine de l’expérimentation EVRY 2004

Nous distinguons maintenant deux sous-classes au sein de la classe C. D’une part, des exercices peu rentables car ne rapportant pas beaucoup de points : ils ont un indice de difficulté élevé comme l’exercice Pente et gradient d’ORSAY 2003 et l’exercice Coïncidence Libre version courbe d’EVRY 2004 et se situent dans la zone de gauche en haut dans les graphiques de profils d'exercices (figures 10 et 11). D’autre part, nous distinguons des exercices peu rentables car nécessitant beaucoup de temps comme l’exercice Coïncidence Libre version affine d’EVRY 2004. Ils ont un indice de difficulté faible et se situent dans la zone de gauche en bas.

a) Les exercices Pente et gradient et Coïncidence Libre version courbe ont des indices de difficulté élevés comparativement aux autres exercices de l’expérimentation d’où ils sont issus : 88/36=2,44 et 55/8=6,87 respectivement. Le nombre total de points pour ces exercices est faible. Comparons-les respectivement aux exercices Dérivées partielles 1 et Droite animée :

Tableau 11 : Comparaison de données traitées globales Dérivées partielles 1 et Pente et gradient

Tableau 12 : Comparaison de données traitées globales Droite animée et Coïncidence courbe

Ces exercices de classe C, dont l’indice de difficulté est élevé, sont autant travaillés, voire plus, que les exercices de classe A. C’est-à-dire qu’il y a une volonté manifeste des étudiants à vouloir se confronter à ces exercices. Cependant, ces exercices, pour les étudiants qui proposent des résultats, sont ceux qui demandent le plus de temps aux étudiants pour qu’ils soumettent un résultat (notamment à la première rencontre) et ce sont les exercices qui rapportent le moins de points. Enfin, pour les quelques étudiants qui font l’exercice plus de trois fois, la moyenne des trois dernières notes n’est pas sensiblement meilleure que celle des trois premières. Il existe parfois de longues suites de scores 0 dans les journaux de traces. Notons que quelques étudiants abandonnent tout de même l’exercice très rapidement sans véritablement le chercher. Ils préfèrent augmenter leurs moyennes sur des exercices de classe A. L’observation en séance montre que les étudiants ont besoin d’une aide pour amorcer la résolution de l’exercice. Quand elle existe, celle du logiciel semble insuffisante : elle donne par exemple l’indication qu’il faut penser au gradient dans l’exercice Pente et gradient, ce qui est déjà en germe dans le titre de l’exercice.

Pour le concepteur, une réflexion pourrait être entamée sur l’activation d’une aide automatique après 2 mauvaises notes, par exemple. L’aide pourrait être alors une aide de cours, décontextualisée de l’exercice. Une deuxième aide pourrait ensuite apparaître, toujours automatiquement et après 2 autres mauvaises notes. Elle pourrait être alors plus contextualisée à l’exercice, en proposant une méthode explicite de résolution. Dans l’état actuel des choses, une aide venant de l’enseignant paraît nécessaire aux étudiants.

De son côté, le didacticien a besoin de savoir quelle est l’activité précise de l’étudiant pendant les minutes de recherche qui mènent à ces notes quasi nulles. Pour ces exercices, il nous apparaît donc nécessaire de faire une observation fine de l’activité réelle des étudiants qui va au-delà de l’étude des journaux de traces en tenant compte du déroulement effectif des séances (aides de l’enseignant, échanges entre étudiants notamment) représenté à la figure 8.

b) L’exercice Coïncidence Libre version affine est un exercice de classe C dont l’indice de difficulté est plus faible comparativement aux exercices de l’expérimentation EVRY 2004 : 300/91=3,29. Au contraire des deux exercices précédents, c’est le temps passé par les étudiants sur cet exercice qui le catégorise en classe C : près de 45 minutes par étudiant, à comparer avec 6mn11 et 8mn27 pour les exercices Droite animée et Coïncidence Libre version courbe.

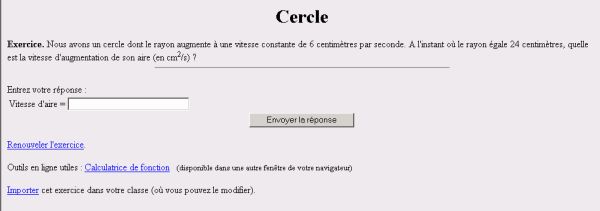
Tableau 13 : Extrait de données traitées globales de l’exercice Coïncidence Libre version affine

Ceci étant, 13 des 22 étudiants font plus de trois fois l’exercice et la moyenne calculée sur ces 13 étudiants est assez bonne. C’est-à-dire que ces exercices sont finalement assez réussis mais il faut énormément de temps aux étudiants. A nouveau, une observation fine de l’activité des étudiants qui va au-delà de l’étude des journaux de traces, nous semble nécessaire pour comprendre pourquoi ces exercices nécessitent tant de temps de travail, ce que font réellement les étudiants pendant tout ce temps où rien n’apparaît sur les traces et pourquoi les exercices sont réussis, chez certains étudiants, à un certain moment.

6.3.3. Les exercices de la classe B, difficiles mais globalement bien réussis

Ce sont les exercices les plus difficiles à analyser à tous points de vue. Du côté des tâches, celles-ci semblent très variées. L’exercice 4 dans l’expérimentation ORSAY 2003, on l’a vu, est uniquement technique mais il n’est pas immédiat du fait notamment de sa longueur. Dans l’expérimentation d’ORSAY 2004, nous donnons l’exemple de trois exercices particuliers que nous reverrons dans le paragraphe suivant : Cercle, Tour et Triangle. Voici un énoncé de l'exercice Cercle :

Figure 14 : Exercice Cercle de l’expérimentation EVRY 2004

Dans cet exercice, l’étudiant doit adapter ses connaissances sur les fonctions numériques en les utilisant comme outils et traduire la situation donnée de la langue naturelle vers le registre des équations fonctionnelles. Il doit ensuite reconnaître la composée de fonctions au moment où il dérive pour déterminer la vitesse d’aire .

L’exercice Tour est présenté de la même façon. Un énoncé précis en est : Quelqu’un marche vers une tour à une vitesse constante de 1,8 mètres par seconde. Si la hauteur de la tour est de 150 mètres, à quelle vitesse (en m/s) la distance entre l’homme et le sommet de la tour diminue quand la distance entre l’homme et le pied de la tour est de 173 mètres ? Dans cet exercice, l’étudiant doit modéliser la situation en mobilisant le théorème de Pythagore. Il doit ensuite à nouveau reconnaître les composées de fonctions au moment où il dérive la formule pour obtenir .

Enfin, l’exercice Triangle est une version déjà modélisée de l’exercice Tour avec dans ses énoncés le dessin d’un triangle rectangle où est matérialisé l’angle droit : Nous avons un triangle rectangle comme suit, où AB=54cm et AC augmente à une vitesse constante de 5cm/s. Au moment où AC=27cm, quelle est la vitesse du changement de BC (en cm/s) ?

Les exercices de la classe B sont très différemment réussis et les moyennes ou les totaux de données traitées marquent de grandes disparités. C’est ici que l’on trouve les exercices les plus tentés et ceux pour lesquels le plus de résultats sont soumis. La durée de travail et le nombre de points obtenus sont aussi parmi les plus élevés mais ce ne sont pas les exercices qui nécessitent le plus de temps pour une réponse. Compte tenu de notre schéma théorique, on peut tout de même conclure que les exercices de classe B sont intéressants du point de vue de l’apprentissage des étudiants. En effet, les tâches dépassent les applications immédiates de connaissances et la rentabilité globalement bonne traduit une activité réelle riche des étudiants. Ces exercices de la classe B sont l’objet de notre attention dans le paragraphe suivant.

7. Impact du scénario sur les exercices de la classe B

Dans cette dernière partie, nous cherchons à expliciter et à préciser l’influence du scénario en mettant en évidence des cohérences entre l’activité réelle de plusieurs cohortes d'étudiants et les scénarios associés aux exercices. Une première précaution méthodologique est de nous intéresser seulement aux exercices de la classe B. Nous avons en effet déjà signalé que ces exercices sont importants pour l’apprentissage des étudiants compte tenu de leurs tâches variées. Ceci étant, l’étude des données traitées n’appelle pas, contrairement aux exercices de la classe C, un besoin supplémentaire systématique d’informations sur le déroulement effectif des séances (les aides de l’enseignant et les échanges entre étudiants notamment). Les conclusions de ce paragraphe sont cependant à prendre avec précaution : par exemple, il y a l'hypothèse implicite que les cohortes d'étudiants sont équivalentes d'une année sur l'autre.

7.1. Les deux scénarios dans les expérimentations EVRY 2003 et EVRY 2004

Les trois exercices Cercle, Tour et Triangle ont été utilisés dans les expérimentations EVRY 2003 et EVRY 2004 avec deux scénarios différents. Dans les deux cas, ces exercices sont en classe B.

7.1.1. Les trois exercices sont donnés à la suite dans l’expérimentation EVRY 2004

C’est le cas dans l’expérimentation EVRY 2004. L’analyse a priori des tâches et du scénario permet d’inférer que l’enchaînement des trois exercices va avoir une influence sur l’activité des étudiants à chacun des exercices. En effet, la connaissance principale à mettre en fonctionnement dans l’exercice Cercle est la dérivation de la fonction composée en . Il s’agit de la même connaissance qu’il faut mettre en fonctionnement dans les exercices Tour et Triangle au moment de dériver ou . En outre l’exercice Triangle est une version simplifiée de l’exercice Tour. Cette analyse a priori permet donc d’inférer une augmentation de la rentabilité des étudiants dans l’exécution des trois exercices à la suite. Voici cependant des données traitées globales

Tableau 14 : Extrait de données traitées globales pour les exercices Cercle, Tour, et Triangle

et une restriction de ces données traitées aux 6 étudiants qui ont réussi les 3 exercices. Ces 6 étudiants ont bien abordé et réussi les exercices dans l’ordre de la feuille de TD-Wims. Il est ainsi significatif de comparer les données propres à chaque exercice sur la base de ces 6 étudiants :

Tableau 15 : Données traitées sur 6 étudiants pour les mêmes exercices

L’analyse de l’activité réelle de ces 6 étudiants fait apparaître qu’il n’y a pas du tout de gain de rentabilité entre l’exercice Cercle et l’exercice Tour : les étudiants travaillent autant sur le deuxième exercice que sur le premier pour un total de points inférieur. Plus précisément, ils mettent sensiblement plus de temps à la première rencontre et plus de temps pour obtenir la note maximale de 10. Cela signifie que l’exercice Tour présente par rapport à l’exercice Cercle des adaptations de connaissances plus fines et qu’il convient de revenir sur l’analyse a priori des tâches et les activités attendues pour comprendre pourquoi les étudiants ne profitent pas du travail sur le Cercle en abordant la Tour. Le passage de la Tour au Triangle est plus cohérent avec l’analyse a priori qui met en évidence que le Triangle est une version simplifiée de la Tour : le rendement est sensiblement meilleur, l’indice de difficulté plus faible tandis que les temps à la première rencontre et pour avoir 10 diminuent. Ceci étant, un rapide retour sur les statistiques traitées de l’ensemble des étudiants à ces trois exercices montre que seuls 6 étudiants ont réussi le Triangle alors qu’ils étaient 11 à réussir la Tour. Même si nous avançons sur la classification des adaptations, tout n’est donc pas transparent.

7.1.2. Les trois exercices sont les trois formes aléatoirement prises par un unique exercice

Dans l’expérimentation EVRY 2003, les trois exercices sont donnés aléatoirement au sein d’un même exercice appelé Cercle Tour Triangle. Ce choix se justifie étant donnée la connaissance commune à mettre en fonctionnement dans les trois exercices, à savoir la dérivation de fonctions composées. Le travail sur les trois formes données aléatoirement peut favoriser, par les adaptations qu’il nécessite (reconnaître notamment à chaque fois la composée), l’apprentissage des étudiants autour de cette connaissance, c’est-à-dire une certaine conceptualisation mais aussi l’organisation et l’articulation avec les autres connaissances de l’étudiant. Les statistiques d’activité font cependant apparaître un rendement moins bon qu’aux trois exercices de l’expérimentation EVRY 2004 (1,8 contre 3,09, 1,83 et 2,09) et un indice de difficulté sensiblement plus élevé (1,76 contre 1,30, 1,39 et 1,14).

Tableau 16: Extrait de données traitées globales de l’exercice Cercle Tour Triangle EVRY 2003

Même si les trois exercices mettent en fonctionnement une connaissance identique dans trois contextes différents et avec des adaptations différentes, ces trois contextes et les adaptations semblent trop éloignés les uns des autres pour permettre un travail commun. Une étude particulière de l’activité des binômes fait apparaître des moyennes des trois dernières notes parfois plus faibles que les moyennes des trois premières notes, ce qui traduit la difficulté des étudiants à passer d’une forme à une autre.

On comprend finalement qu’il est dans ce cas préférable de les faire travailler successivement sur les trois exercices puis, peut-être, dans un second temps, de les faire travailler aléatoirement sur l’une des trois formes afin qu’ils mettent en évidence ce caractère commun des formes (ce qui nous semble constitutif d’un apprentissage).

7.2. Les deux scénarios différents dans les expérimentations ORSAY 2003, 2004 et 2005

Nous étudions maintenant deux scénarios mettant en jeu l’exercice Composition II dérivées partielles où il s’agit de déterminer dans un format prédéfini une dérivée partielle seconde d’une fonction composée implicite. Nous avons déjà rencontré cet exercice dans la classe B de l’expérimentation ORSAY 2003. Les statistiques traitées montrent que les étudiants travaillent successivement sur trois exercices progressifs de classe A (à partir de Dérivée partielle 1) puis abordent l’exercice de classe B visé Composition II dérivées partielles. Dans les expérimentations 2004 et 2005, les étudiants travaillent directement sur l’exercice visé. Les statistiques d’activité mettent en évidence le rendement moindre, l’indice de difficulté plus élevé et les moyennes moins bonnes, si bien que l’exercice passe dans la classe C avec le scénario de ces deux dernières expérimentations.

Tableau 17 : Comparaison des données traitées globales Composition II dérivées partielles

Le temps de travail moyen par étudiant est cependant beaucoup plus élevé en 2004 et 2005 : les étudiants rattrapent presque exactement sur le seul exercice Composition II dérivées partielles le temps de travail passé en 2003 sur les trois exercices qui le précèdent : 1h36mn04 de travail total sur les 4 exercices de l’expérimentation ORSAY 2003 à comparer avec 1h34mn35 en 2004 et 1h25mn53 en 2005 sur le seul exercice Composition II dérivées partielles.

La conclusion est dans ce cas qu’il semble plus intéressant de faire travailler les étudiants sur l’enchaînement progressif de l’expérimentation ORSAY 2003 que de les faire travailler brutalement sur l’exercice visé. On retombe sur l’idée importante que le travail sur les exercices de la classe A (ici sur les trois exercices qui en 2003 "préparent le terrain" pour l’exercice visé Composition II dérivées partielles) est nécessaire aux étudiants pour leur assurer des bases. Le temps passé sur ces exercices n’est pas du temps perdu puisqu’il est rattrapé lorsque les étudiants en viennent à affronter l’exercice plus riche. Ceci étant, le choix du scénario dépend de l'objectif visé par l'enseignant en fonction de sa progression ; notre conclusion ne se veut pas prescriptive mais instructive.

8. Conclusion

La question de départ était : que peut apporter l’étude des fichiers de traces pour les différents métiers de l’enseignement utilisant une plate-forme ?

Les premiers résultats montrent l’investissement important des étudiants dans le travail sur machine, ce qui justifie a posteriori la production, l’utilisation et les recherches relatives aux plates-formes d’exercices en ligne. Il apparaît très tôt également une différence d’utilisation suivant les utilisateurs étudiants, ce qui justifie une étude de parcours individuels. C’est un axe sur lequel d’autres chercheurs sont déjà engagés sur des contenus mathématiques plus limités. Les seuls pas que nous ayons faits dans cette direction sont au paragraphe 4.2 et nous poursuivons notre travail dans ce sens. Dans cet article, nous avons travaillé essentiellement avec les moyennes d’activités de groupes d'étudiants, cherchant à éclairer d’abord des différences suivant les types d’exercices et suivant les scénarios.

Les indices de rendement et de difficulté construits à partir des traces d’activités réelles nous ont permis une classification des exercices cohérente avec les analyses de tâches a priori. Les avantages de cette classification sont multiples. Elle prend en compte le contenu de l’exercice mais sans pour autant être dépendante d’un chapitre spécifique. Elle peut donc concerner un domaine mathématique vaste. Elle insiste bien sur l’importance d’étudier un exercice dans un contexte précis, c'est-à-dire à l’intérieur d’un scénario. Si ce dernier est le même, la classification semble stable d’une expérimentation à l’autre. Nous avons d’ailleurs pu préciser, sur deux exemples, l’impact du scénario sur l’activité réelle des étudiants. Cette classification permet enfin de préciser et d’organiser nos conclusions ainsi que d’ouvrir des perspectives pour chacun des trois métiers que nous avons retenus : le concepteur, le didacticien et l’enseignant.

Pour le concepteur, la classification montre d’abord qu’il n’y a pas dans les expérimentations étudiées de  "mauvaise" utilisation du logiciel Wims, au sens d’exercices qui seraient très rentables et pourtant très difficiles donc pourraient rapporter des points avec des réponses au hasard. Elle suggère ensuite des adaptations suivant le type d’exercice : pour les exercices de classe A, limiter l’effet "scoring", en interdisant de les chercher trop souvent à partir du moment où ils sont réussis de manière sûre ; pour les exercices repérés de classe C, prévoir l’activation, après plusieurs échecs, d’une aide à déterminer avec le didacticien.

La cohérence entre l’analyse a priori des exercices et l’analyse des activités effectives conforte le didacticien dans la consistance de ses analyses de tâches, leur importance et leur efficacité mais l’engage aussi à affiner, sur des cas précis, l’analyse de tâches en repérant plus finement les processus de résolution. En particulier, sur les exercices de classe C, une investigation supplémentaire est nécessaire en utilisant d’autres outils comme des observations in situ ou des analyses d’enregistrement audio et vidéo. Nous allons poursuivre nos recherches par l’étude des aides de l’enseignant et entre étudiants lors des résolutions de ces exercices difficiles. Par ailleurs, la nécessité de prendre en compte le scénario dans les analyses, particulièrement pour les exercices de classe B, est aussi clairement mise en évidence. Nous allons également continuer à travailler cet aspect en essayant de classifier des adaptations de connaissances et trouver des scénarios qui favorisent leurs meilleurs franchissements par les étudiants.

Pour l’enseignant, un certain nombre de données, indépendantes d’un chapitre ou d’un niveau de mathématiques précis sont à retenir. La nécessité de faire un nombre suffisant d’exercices de classe A. On a vu que sur ces exercices l’apprentissage est visible, rapide mais nécessaire. Or de tels exercices ne sont pas toujours proposés aux étudiants. Ils peuvent être jugés fastidieux ou inutiles alors, qu’au contraire, nous avons montré qu’ils permettaient d’aborder plus efficacement des exercices de classe B. De plus, les étudiants peuvent travailler seuls en dehors des séances collectives sur de tels exercices faciles ; il est donc simplement utile de les prévoir dans un parcours d’apprenant. Pour les exercices de classe B, l’effet de différents types de scénario engage l’enseignant à un choix réfléchi en fonction des objectifs visés. Enfin, un temps et une attention suffisants doivent être dégagés pour les exercices de classe C. Ainsi, les trois catégories d’exercices permettent de réguler les temps d’enseignement.

Nous avons donc vu comment cette classification simple, en trois classes, une fois prouvée sa consistance et sa généralité, permet de renseigner et d’offrir des perspectives au concepteur, au didacticien et à l’enseignant utilisateur. Un récent document produit dans le cadre du projet DPULS (Design Pattern for recording and analysing Usage of Learning Systems) (Gilbert-Darras et al., 2005) identifie plus précisément trois principaux buts aux analyses de traces : la régulation du système d’apprentissage, l’évaluation des apprenants et la validation d’hypothèses de recherches. La classification des exercices de mathématiques, à l’intérieur d’un scénario, en trois classes, permet d’avancer dans l’analyse des traces pour ces trois buts. Nous avons vu une structuration possible du temps d’enseignement mais plus généralement, la régulation du système d’apprentissage et l’évaluation des apprenants ne peut se faire uniformément sans tenir compte de ces trois classes : limitation quantitative de l’activité et gestion des scores pour des exercices de classe A, gestion des aides et évaluation particulière pour les exercices de classe C, réflexion sur les scénarios à partir des exercices de classe B...

Dès qu’indice de difficulté et rendement peuvent être définis, ces trois classes peuvent sûrement être établies. Il suffirait donc de réfléchir, pour d’autres expérimentations du même type, aux relevés minimaux de traces permettant la définition de ces indicateurs et permettant la classification, facilement lisible et exploitable. Si notre définition de l’indicateur de difficulté (nombre de new sur nombre de scores) semble très spécifique du logiciel Wims et doit être réinventée pour d’autres plates-formes d’exercices, il en est tout autrement du rendement puisque les traces semblent toujours rapporter des indicateurs d’évaluations et des temps passés pour répondre aux questions. Si bien que la simplicité des deux indices proposés permet d’envisager une généralisation de la méthode, à un coût faible, pour des enseignements sur plate-forme proposant des exercices.

BIBLIOGRAPHIE

BISSON G., BRONNER A., GORDON M.B., NICAUD J.F., RENAUDIE D. (2003). Analyse statistique de comportements d’élèves en algèbre. Actes de la conférence E.I.A.H. 2003, pp67-78.

BOUHINEAU D., BRONNER A., CHAACHOUA H., HUGUET T., (2003). Analyse didactique de protocoles obtenus dans un E.I.A.H. Actes de la conférence E.I.A.H. 2003, pp79-90.

BROUSSEAU G., (1997). Theory of didactical situations in mathematics, Edited by Nicolas Balacheff, Mathematics Education Library, Kluwer Academic Publishers.

DIEUMEGARD G., CLOUAIRE P., PARIS P., (2004). L’organisation temporelle de l’activité des apprenants en e-formation Actes du colloque TICE 04, p 362- 368.

DOUADY R., (1986). Jeux de cadres et dialectique outil-objet, Recherche en didactique des mathématiques, 7(2) : p 5-31.

DUVAL, R., (1993). Registres de représentations sémiotique et fonctionnement cognitif de la pensée, Annales de didactique et de sciences cognitives, numéro 5, p 37-65 Publication de l’IREM de Strasbourg.

GILBERT-DARRAS F., DELOZANNE E., LE CALVEZ F., MERCERON A., LABAT J.M., VANDEBROUCK F., (2005). Towards a design pattern language to track students’problem-solving abilities, workshop proceeding of the 12th International Conference on Artificial Intelligence in Education AIED 2005, Amterdam, The Netherlands, IOS Press, 2005

GODINET H. (2003). L’accompagnement dans le campus numérique FORSE: modalités et outils in Actes de la conférence EIAH 2003, Environnements Informatiques pour l'Apprentissage Humain pp 223-234.

GUERAUD V., ADAM J-M., PERNIN J-P., CALVARY G., DAVID J-P. (2004). L'exploitation d'objets pédagogiques interactifs à distance : le projet FORMID, STICEF Volume 11, 2004.

GUERAUD V., CAGNAT J-M. (2004). Suivi à distance de classe virtuelle active Actes du colloque TICE 2004 p 377- 383.

LINARD M. (2003). Autoformation, éthique et technologie : enjeux et paradoxes de l’autonomie. In Autoformation et enseignement supérieur, Albéro B. Hermes.

MAZZA, R, (2003). Using open student models in distance learning environments to help teachers provide adaptive tutoring, SCOMS-Studies in Communication Sciences, Special Issue New Media In Education, March 2003, pp 245-251 ISSN 1424-4896.

MAZZA, R, DIMITROVA V., (2004). Visualising Student tracking Data to Support Instructors in Web-based Distance Education, 13^th International Word Wibe Web Conference (WWW 2004) May 17-22 2004, New-York.

MERCERON A. YACEF K. (2004). Train, store, analyse for more adaptative teaching, Acte du colloque TICE 2004 , 52-58.

MERCERON A. YACEF K. (2004). Mining student data captured from a web-based tutoring tool : initial exploration and results, Journal of interactive learning research, 15(4) 319-346.

RAMAGE M-J., PERRIN B. (2004). La technologie au service de pratiques d'apprentissage différenciées : la plate-forme WIMS, utilisation en premier cycle universitaire. Actes du colloque TICE 2004 pp 121-126.

ROBERT A. (1998). Outils d’analyse des contenus mathématiques à enseigner au lycée et à l’université. Recherches en didactique des mathématiques. 18(2) : p 139-190.

ROBERT A., ROGALSKI M. (2002). Comment peuvent varier les activités mathématiques des élèves sur des exercices ? Le double travail de l’enseignant sur les énoncés et sur la gestion en classe. « Petit x » 60 : p 6-25.

RUTHVEN K., HENESSY S. (2002). A practitioner model of the use of computer-based tools and resources to support mathematics teaching and learning, Educational studies in mathematics, 49 (2-3): p 47-86.

Références à des sites Internet

DELOZANNE E., PREVIT D., GRUGEON B., JACOBONI P. (2003). Scénario d’utilisation et conception d’un EIAH, le cas de diagnostique dans pépite. Actes du colloque ITEM, IUFM de Reims. http://www.reims.iufm.fr/Recherche/ereca/itemcom/

XIAO G. (2000). Interactive Mathematics Server Journal of online Mathematics and its applications. http://www.jama.org/articles/xiao/xiaotop/html

A propos des auteurs

Claire CAZES, ancienne élève de l’École Normale Supérieure, est maître de conférences à l’Université Pierre et Marie Curie. Elle a soutenu une thèse en didactique des Mathématiques sur l’enseignement des suites numériques en enseignement à distance. Elle s'est fortement impliquée dans les utilisations pédagogiques de l’informatique et du multimédia pour encourager de nouvelles formes d’enseignement notamment dans le campus numérique C@mpusciences. Membre de l’équipe DIDIREM de l’Université Paris VII, elle participe notamment au sein du réseau d’excellence européen Kaleidoscope à l’équipe TELMA ( Technology Enhanced Learning in Mathematics).

Adresse : Université Paris 7, Equipe de recherche Didirem,Case Courrier 7018 2 place Jussieu 75251 Paris Cedex 5

Courriel : cazes@ccr.jussieu.fr

Fabrice VANDEBROUCK est maître de conférences à l’Institut Universitaire de Formation des Maîtres de Versailles. Agrégé et docteur en mathématiques, il enseigne en Licence et à la préparation au CAPES de l’Université d’Evry Val d’Essonne. Il est membre du bureau de l’équipe de recherche DIDIREM de l’Université Paris 7 et s’intéresse à l’intégration des nouvelles technologies dans l’enseignement supérieur. Il participe au sein du réseau Kaleidoscope à l’équipe TELMA (Technology Enhanced Learning in Mathematics) et au projet DPULS (Design Pattern for recording and analysing Usage of Learning Systems). Enfin, il participe au projet GUPTEN (Génèse d’Usages Professionnels des Technologies dans l’Enseignement).

Adresse : Université Paris 7, Equipe de recherche Didirem, Case Courrier 7018 2 place Jussieu 75251 Paris Cedex 5

Courriel : fabrice.vandebrouck@univ-evry.fr

Référence de l'article :

Fabrice Vandebrouck, Claire Cazes , Analyse de fichiers de traces d’étudiants : aspects didactiques, Revue STICEF, Volume 12, 2005, ISSN : 1764-7223, mis en ligne le 18/01/2006, http://sticef.org