Sciences et Technologies
Sciences et Technologiesde l´Information et
de la Communication pour
l´Éducation et la Formation
version à télécharger (pdf)
Volume 11, 2004
Article de recherche
|
Contact : infos@sticef.org |
Approche
ontologique et navigation
|
|
|
|
|
|
|
- 1. Introduction
- 2. Catégorisation et apprentissage
- 3. Un EIAH pour l’enseignement des statistiques en psychologie
- 4. Réalisation et navigation dans l’EIAH
- 5. Discussion et perspectives.
- Références
1. Introduction
Les modes traditionnels de transmission des connaissances induisent des contraintes évidentes de linéarité de présentation qui sont à mettre en regard avec la manière dont les connaissances sont structurées en mémoire, structuration qui est au cœur de leur utilisation. En particulier, ces modes de transmission conduisent l’enseignant à privilégier un point de vue et permettent rarement d’expliciter la coexistence de plusieurs points de vue sur la matière à enseigner. Ainsi, dans le domaine de connaissances considéré dans cet article, les statistiques pour psychologues, on peut aborder la matière du point de vue des concepts à enseigner (notion de variable, de protocole, etc.) ou du point de vue des buts et des procédures applicables à ces objets (ce qui peut être fait et comment cela peut être fait). Les modes traditionnels de présentation des contenus de connaissances, en linéarisant des contenus structurés en mémoire de l’enseignant, rendent difficile l’articulation des concepts par un apprenant qui devra les structurer à nouveau à partir de cette présentation linéaire sur la base de relations pas nécessairement explicitées. Cette reconstruction est d’autant plus difficile lorsque plusieurs points de vue coexistent, comme c’est le cas par exemple pour les statistiques. Si le constat de ce processus de déconstruction-reconstruction ne devrait pas incliner à tirer des conclusions simplistes, il invite toutefois à prendre en compte que la linéarité du parcours n’a, du fait du développement des hypermédias, plus caractère de nécessité et que sa structuration est devenue une variable didactique pouvant être manipulée dans un EIAH.
L’objectif de cet article est de montrer que les résultats de travaux en psychologie cognitive invitent, pour certains contenus disciplinaires, à utiliser une ontologie ou tout au moins une composante d’une ontologie, sous la forme d’un réseau sémantique organisé selon la relation d’inclusion de classes comme support de navigation dans un EIAH. Cela permet tout à la fois d’expliciter les concepts à acquérir et de favoriser l’acquisition des relations d’inclusion de classes qui constituent une dimension fondamentale des apprentissages car elles sont un des éléments essentiels dans la production d’inférences (section 2), et à ce titre constituent un des critères distinctifs entre les novices et les experts. Ces relations d’inclusion de classes sont également un des éléments essentiels participants à la flexibilité cognitive de l’expert, notamment à travers le phénomène de marquage et à son efficacité cognitive, à travers l’articulation entre la structuration rationnelle et la structuration fonctionnelle des connaissances (section 2.4 et section 3).
La construction d’un tel EIAH rend envisageable de viser un cursus d’apprentissage qui explicite et intègre, par une navigation à l’intérieur d’une ontologie, l’organisation cognitive visée. S’il n’est guère probable que la seule exploration d’un réseau sémantique soit, de manière isolée, un facteur d’apprentissage, cela semble en revanche être une voie prometteuse que d’intégrer de telles explicitations à un cursus d’apprentissage, pour prendre en compte les données de la psychologie cognitive sur l’organisation et l’utilisation des connaissances. Un EIAH fondé sur ces principes est en cours de développement dans le cadre de l’enseignement à distance des statistiques en psychologie à l’I.E.D. (Institut d’Enseignement à Distance) de l’Université Paris 8. Il sera présenté afin d’illustrer la démarche (section 4).
2. Catégorisation et apprentissage
2.1. La catégorisation comme outil de classification et d’inférence
Comme l’ont noté, avec d’autres, ([TverskyHemenway91], p. 439), "le monde nous présente un nombre incalculable de choses différentes. Une manière pour les gens d’affronter cette diversité, tout en y mettant de l’ordre, est de grouper les choses similaires en catégories et les catégories en taxonomies". Outre cette fonction de classification, la catégorisation permet d’inférer des propriétés non observables à partir de propriétés observables. Par exemple, catégoriser une entité comme chien, permet d’inférer qu’il est susceptible d’aboyer, de mordre, d’aller chercher un os, qu’il a un cerveau, un estomac, etc. ; autant de caractéristiques qui n’auront pourtant pas été effectivement observées sur ce chien particulier [MurphyRoss94]. A ce titre, la catégorisation constitue un support de raisonnement et d’action du fait de sa fonction prédictive [Anderson91]. Par exemple, [BlessingRoss96] ont montré que les apprenants qui identifiaient une catégorie d’appartenance au problème à résoudre (ex : problème de mélange) avaient des comportements très différents de ceux qui ne le faisaient pas : ils mettaient immédiatement en œuvre les procédures de résolution pertinentes alors que les autres se lançaient dans une analyse laborieuse du problème. Ainsi, la construction de catégories pertinentes et d’indices d’accès à ces catégories constitue des dimensions fondamentales des apprentissages [Holyoak85], [HolyoakKoh87], [Sander00], [Sander03]. Les traits saillants d’une situation [Vosnadiou89], [BlessingRoss96], [RichardSander00] sont utilisés comme indice d’accès à une catégorie et permettent alors d’accéder aux autres informations associées, notamment des connaissances déclaratives, des procédures et des mises en relation avec des catégories sémantiquement liées [Tijus96].
2.2. Différence de catégorisation selon le niveau de connaissance sur un domaine
Novices et experts d’un domaine diffèrent dans leurs catégorisations : les novices, contrairement aux experts, incluent essentiellement des informations superficielles dans leurs critères de catégorisation, comme les objets spécifiques, les termes utilisés, la forme de la question [Adelson81], [ChiAl81], [ChiAl82], [SchoenfeldHerrmann82], [Silver79], [Silver81]. Dans un article classique, [ChiAl81] ont montré que les novices en physique regroupent des problèmes faisant intervenir les mêmes objets, comme des problèmes de poulie ou de plan incliné alors que les experts tiennent aussi compte de ces traits de surface, mais regroupent les problèmes selon le principe physique mis en jeu, par exemple la troisième loi de Newton. Des résultats convergents ont été trouvés par [HardimanAl89] avec une tâche d’évaluation de similitude entre problèmes de physique et [Silver79], [Silver81] a trouvé des résultats similaires pour des problèmes mathématiques. [SchoenfeldHerrmann82] ont montré que des étudiants classant des problèmes en fonction de caractéristiques de surface des objets décrits modifiaient leur méthode de classement et prenaient en compte les principes de résolution après avoir suivi un enseignement de mathématiques. [ChiAl89] ainsi que [ChiVanLehn91] ont montré également que les "bons apprenants" sont ceux qui catégorisent les exercices en fonction des buts réalisés et des conditions de réalisation de ces buts.
D’autres travaux montrent l’influence de l’expertise sur la catégorisation en s’inscrivant dans un paradigme différent. Depuis les recherches princeps de Rosch [Rosch78], [Cordier93], [RoschAl76], [MedinAl00], on sait que plusieurs mesures, qu’elles soient perceptives ou fonctionnelles, convergent vers un niveau de catégorisation particulier : le niveau de base, qui est le niveau le plus abstrait pour lequel les membres de la catégorie ont des formes similaires et reconnaissables. C’est aussi un niveau choisi préférentiellement lors de la dénomination et également le plus informatif car les sujets donnent nettement plus d’attributs pour définir ce niveau qu’ils ne le font pour définir celui directement superordonné, alors qu’ils ne donnent que peu d’attributs supplémentaires pour définir un niveau subordonné. [TanakaTaylor91] montrent pourtant que le niveau privilégié de catégorisation n’est pas obtenu par des critères indépendants de l’observateur. Ainsi des experts en chiens et en oiseaux catégorisent à la même vitesse au niveau subordonné et au niveau de base, et plus lentement au niveau superordonné, alors qu'on retrouve chez les novices une catégorisation plus rapide au niveau de base qu’au niveau superordonné. Le même effet est noté pour la dénomination : les experts ont tendance à dénommer autant au niveau subordonné qu’au niveau de base, contrairement aux novices qui dénommeront plus rapidement au niveau de base. Ces résultats ont été confirmés par des expériences de [JohnsonMervis97] montrant que les meilleurs experts pouvaient traiter comme un niveau de base des niveaux ayant deux degrés de subordination par rapport au niveau de base pour un novice.
2.3. Le statut particulier de la relation d’inclusion de classes.
Les théories de la représentation des connaissances en mémoire considèrent toutes que la relation général-spécifique, ou relation d’inclusion de classes ("est un", "est une sorte de") est une relation essentielle [CollinsLoftus75]. Des travaux déjà anciens ont établi que les listes organisées en taxonomies sont mieux rappelées que les listes de mots non liés [BowerAl69], [Puff70] et la littérature sur les associations libres a indiqué que le mot le plus fréquemment associé à de nombreux mots est souvent un nom de catégorie superordonnée (e.g. chaise comme stimulus donne meuble). Comme le note [Barsalou83], c’est parce que des structures bien établies en mémoire mettent en relation ces catégories que les catégories superordonnées sont hautement associées. Cette relation a un statut particulier du fait des traitements cognitifs qu’elle autorise : l’organisation selon une hiérarchie général-spécifique indique le nombre de points de vue qu’il est possible de prendre sur un même objet en le considérant à différents niveaux d’abstraction, du plus spécifique au plus général et offre ainsi une mesure de flexibilité des points de vue qui pourront être pris selon le contexte. Par exemple [SanderRichard98], un même objet peut être catégorisé comme une Nike, de tel modèle et de telle taille (par un vendeur durant l’inventaire de sa boutique), comme une Nike (par un client au supermarché), comme une chaussure de sport (par quelqu’un qui va courir), comme une chaussure (par quelqu’un qui cherche des chaussures), comme un produit manufacturé (par un statisticien qui travaille sur la consommation des ménages) etc. [RichardSander00] ont montré, dans le cadre de la résolution de problèmes de mathématiques, que le niveau d’abstraction de la catégorisation d’un problème était un déterminant essentiel du transfert d’apprentissage (voir aussi, [BassokOlseth95], [BassokAl95], [Bassok01]). Ainsi, la réussite du transfert entre deux problèmes isomorphes de mélanges [Reed87], l’un de mélange de solutions chimiques (Une infirmière mélange une solution de 6% d’acide borique avec une solution de 12% d’acide borique. Combien lui faut-il de chaque solution pour avoir 4,5 litres de mélange à 8%?), et l’autre de "mélange" de taux d’intérêts entre différents comptes bancaires (M. Roberts reçoit 7% d’intérêts comme revenu de ses actions et 11% d’intérêts de ses bons du Trésor. Combien a-t-il sur chaque compte, sachant qu’il a au total 8000 francs et qu’il a eu en moyenne 8% d’intérêts?) semble dépendre de ce que la catégorie construite pour coder le premier problème est ou non suffisamment abstraite pour inclure le second (voir Figure 1).
Figure 1 : Trois niveaux de catégorisation possibles organisés de manière hiérarchique
Ainsi si le problème de mélange d’acides boriques est catégorisé au niveau le plus abstrait, c’est-à-dire comme une situation de combinaison, dont le mélange avec dissolution des composants n’est qu’un cas particulier, le transfert avec le problème des comptes est aisé car il s’agit d’appliquer une procédure associée à cette même catégorie. A l’inverse, si le problème de mélange d’acides boriques est catégorisé au niveau subordonné, il n’y a pas de légitimité de transférer la procédure au cas des problèmes de compte et le transfert devrait échouer. Dans ce cas particulier, le transfert est peu élevé car le problème donné en apprentissage est une situation de mélange de substances liquides. Ce type de mélange a une propriété spécifique, c’est qu’une fois l’opération de mélange réalisée, il n’y a plus qu’une substance, celle qui résulte du mélange, et les composants du mélange sont perdus. L’objet auquel s’applique la concentration moyenne est bien identifié physiquement, c’est le résultat du mélange. Lorsqu’on donne en situation de transfert un problème d’intérêt moyen sur deux comptes, on n’a pas de mélange effectif : il existe toujours deux comptes et il n’y a pas de dissolution en un seul compte bancaire. L’objet auquel s’applique l’intérêt moyen est purement virtuel. Il faut le construire : c’est l’ensemble des deux comptes constituant le capital de la personne, et ce n’est pas un compte à proprement parler. Dans ce cas, le transfert ne se fait pas car la propriété pertinente pour le problème cible est plus générale que celle qui a été retenue pour le problème appris et la récupération nécessite la construction de cette propriété. Elle n’est pas reconnue dans le problème appris parce que le problème appris a été catégorisé comme un problème de mélange physique. Le problème cible n’est pas catégorisé spontanément comme un problème de mélange car aucun objet résultant du mélange n’est décrit dans l’énoncé ni naturellement inféré par le sujet. Dans cette situation, le problème est catégorisé à un niveau trop spécifique par la plupart des sujets, ce qui empêche le transfert. Le niveau d’abstraction auquel se réalise la catégorisation est donc essentiel ; à ce sujet le cas de marquage, dans lequel un même terme du lexique est utilisé pour désigner des catégories de niveau d’abstraction variable, est exemplaire.
2.4. Marquage, point de vue inclusif, exclusif et apprentissage
Lune désignait originellement de manière non ambiguë la planète en rotation autour de la Terre et s’écrivait uniquement avec une majuscule. Avec la découverte d’autres planètes satellites, la majuscule a disparu et le terme a pris une acception plus générale [Hofstadter97]. Lune peut être interprété de manière exclusive des autres planètes satellites comme désignant la Lune ou inclusive comme désignant une catégorie superordonnée, si bien qu’il peut être correct de dire que cette lune n’est pas la Lune. Si la subsistance de la majuscule à l’écrit pour la Lune, satellite de la Terre, peut lever l’ambiguïté, seuls les indices contextuels peuvent départager les deux interprétations à l’oral. Le passage d’un point de vue exclusif vers un point de vue inclusif en conservant un même terme du lexique est notamment rendue possible par la polysémie des étiquettes verbales : un même terme peut désigner plusieurs catégories. En particulier, lorsque la même étiquette verbale est utilisée pour désigner plusieurs concepts ordonnés selon la relation d’inclusion [Politzer91]. Ce phénomène de marquage est peu conceptualisé par celui qui en fait usage mais très répandu dans les domaines familiers, dans lesquels le niveau d’abstraction requis est sélectionné en fonction du contexte si bien que la polysémie des termes est le plus souvent ignorée. Par exemple, en fin de repas dans un restaurant, à la question qui veut un café ? on peut répondre thé, infusion, déca, café serré, crème, expresso. Dans ce contexte, un thé est un café. À un niveau intermédiaire café désigne les boissons à base de café. En ce sens, déca, crème, allongé, serré sont des cafés mais pas thé ou infusion. Au niveau spécifique, café désigne le café servi par défaut (que l’on commande au comptoir par exemple) et en ce sens il est exclusif des autres : allongé, déca, crème sont des café2 mais pas des café1 (Figure 2). Si les différents niveaux sont conceptualisés, on peut prendre l’un ou l’autre point de vue selon le contexte. Par exemple si on demande, au comptoir d’un bar : 3 cafés, 1 allongé, 1 déca et 1 crème, deux interprétations sont possibles. Selon le point de vue inclusif (Café 2), on a désigné la catégorie superordonnée avant de spécifier ses instances et ce sont 3 cafés au total qui ont été commandés. Selon le point de vue exclusif (Café 1), les 3 premiers cafés sont exclusifs des 3 autres et il y a donc 6 cafés qui ont été commandés au total.
Figure 2 : Exemple de marquage pour l’étiquette café
On peut citer de nombreux exemples. Ainsi, selon le contexte homme peut inclure ou exclure femme ; animal peut inclure ou exclure homme ; enfant peut inclure ou exclure bébé ou adolescent; grand peut inclure ou exclure très grand ; jour peut inclure ou exclure nuit ; frigidaire peut inclure ou exclure une autre marque de réfrigérateur ; Larousse peut inclure ou exclure une autre marque de dictionnaire, etc.
Les cas de marquage sont très fréquents notamment du fait qu’il est usuel de dénommer une catégorie superordonnée par l’un de ses membres typiques [GlucksbergKeysar90] comme l’illustrent les derniers exemples.
L’identification de ce phénomène est fondamentale pour étudier les apprentissages. En effet, l’usage d’un terme n’est pas révélateur du fait que le concept sous-jacent a été construit à un niveau inclusif et il est possible que seuls les niveaux exclusifs existent. Ainsi, [SanderAl02] ont fait l’hypothèse qu’un domaine de connaissance se construit en privilégiant d’abord les points de vue exclusifs pour les catégories à faible profondeur et les points de vue inclusifs pour les catégories avec un fort degré de profondeur. Dans la structuration la plus simple, il y a une catégorie générale (Genre) et un ensemble de sous catégories définies de manière exclusive (Espèces). Une structuration simple, c’est-à-dire avec beaucoup de feuilles, peu de nœuds, et peu de niveaux d’abstraction, est privilégiée. En termes d’efficience cognitive, une structuration simple des connaissances (avec peu de nœuds) permet de réaliser une fonction fondamentale de la catégorisation, particulièrement lors de la découverte d’un domaine : distinguer. Ainsi, un novice en figures géométriques va organiser la catégorisation autour du genre "quadrilatères", et d’espèces de quadrilatères : les trapèzes, les parallélogrammes, les rectangles, les losanges, les carrés. Cette organisation se fait au détriment des niveaux intermédiaires, qui n’existent pas (ne sont pas conceptualisés) et/ou dont les étiquettes servent uniquement pour des concepts spécifiques (point de vue exclusif). Par exemple, rectangle sert d’étiquette uniquement pour un rectangle non carré; parallélogramme uniquement pour un parallélogramme non losange et non rectangle (Figure 3).
Figure 3 : Réseau sémantique des quadrilatères à deux niveaux d’abstraction
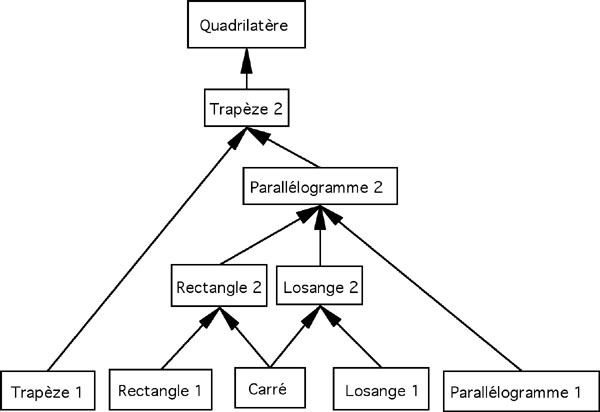
[SanderAl02] ont cherché à montrer que, au fur et à mesure de l’acquisition d’expertise sur un domaine, les dimensions inclusives se développent en ajoutant des catégories intermédiaires (des genres intermédiaires), fréquemment en lexicalisant une catégorie plus générale par un terme utilisé pour une catégorie plus spécifique [Politzer91]. Ainsi, à un niveau intermédiaire d’expertise pour les quadrilatères, un apprenant est susceptible d’avoir 3 niveaux d’inclusion (Figure 4) alors que l’expert aura structuré ses connaissances selon les 5 niveaux d’abstraction (Figure 5).
Figure 4 : Réseau sémantique des quadrilatères à trois niveaux d’abstraction
Figure 5 : Réseau sémantique des quadrilatères à cinq niveaux d’abstraction
Figure 6 : Réseau sémantique des quadrilatères faisant apparaître le marquage
En fait, en raison du marquage, rectangle peut être utilisé dans le sens marqué de rectangle non carré (rectangle1) ou dans le sens non marqué de rectangle (rectangle2), c’est également le cas pour les autres figures (Figure 6). Du point de vue de l’identification et de l’acquisition des connaissances, une conséquence du marquage est que l’identité lexicale conduit à ce que l’absence d’une catégorie puisse être difficile à identifier dans la mesure où l’étiquette verbale est présente, sans que nécessairement les concept1 et concept2 le soient. Par exemple, si seul rectangle1 est présent, l’apprenant ou l’enseignant n’est susceptible de se rendre compte de l’absence de rectangle2 que dans les cas de rectangle2 qui ne sont pas des rectangle1, c’est-à-dire lorsque les carrés ne sont pas vus comme des rectangles.
Les descriptions précédentes montrent que le nombre de catégories n’est pas le critère essentiel : c’est la structuration qui détermine les possibilités d’inférences et d’actions. En termes d’efficience, disposer de plusieurs niveaux d’abstraction offre
-
une plus grande flexibilité dans la mesure où il devient possible, en fonction du contexte, de prendre différents points de vue sur un même objet du monde ;
-
la possibilité de faire des inférences par héritage de propriétés. La profondeur accroît les possibilités d’inférences dans la mesure où une catégorie subordonnée hérite des propriétés des catégories superordonnées ;
-
la possibilité par le marquage de conserver le point de vue exclusif quand il est pertinent, sans ajout d’étiquette verbale.
Ainsi, dans les différents réseaux sémantiques précédents, le nombre de catégories est constant d’un réseau à l’autre si l’on ne prend pas en compte les catégories marquées, alors que les inférences possibles varient grandement. Par exemple, le carré de la Figure 3 n’hérite que des propriétés du quadrilatère, alors que, dans le réseau de la Figure 5, le carré hérite du parallélogramme d’avoir ses diagonales qui se coupent en leur milieu, du rectangle qu’elles soient de même longueur et du losange qu’elles soient perpendiculaires.
Les résultats expérimentaux de cette recherche ont porté sur plusieurs tâches :
-
Explicitation d’inclusion de classes. Par exemple, est-ce qu'un carré est un rectangle particulier ?, Est-ce qu'un carré est un losange particulier ? Est-ce qu'un rectangle est un parallélogramme particulier ?
-
Dénomination d’instances. Par exemple, peut-on dire de cet objet que c’est un carré, un rectangle, un losange, etc ?
-
Explicitation de propriétés : quelle est la définition d’un carré, d’un rectangle, d’un losange, etc ?
Ils ont montré que les points de vue exclusifs dominent tant chez des collégiens qui ont étudié récemment les quadrilatères que chez des adultes, étudiants à l’université : un carré est considéré comme n’étant ni un rectangle ni un losange. Ce point de vue est observé y compris dans les définitions des figures pour lesquelles des propriétés sont fréquemment ajoutées, par exemple en intégrant abusivement à la définition d’un rectangle que ses côtés ne peuvent pas être égaux ou à celle d’un losange qu’il n’a pas d’angle droit. Ainsi cette recherche a montré que les relations d’inclusions de classe ne sont pas acquises pour ces objets, pourtant considérés comme relevant de l’enseignement élémentaire ; elle invite à envisager des modes d’apprentissage favorisant l’acquisition des relations entre catégories.
3. Un EIAH pour l’enseignement des statistiques en psychologie
Quel intérêt peut avoir la prise en considération de ces données sur la catégorisation dans la construction d’un EIAH ? Concernant l’implication de ce point de vue pour les acquisitions de connaissances, nous défendons l’idée que l’explicitation et la navigation dans des réseaux sémantiques peuvent constituer des apports décisifs à condition bien évidemment de ne pas être dissociées de cursus d’apprentissage adaptés. Comme le montrent les travaux précédemment cités sur la catégorisation, la connaissance des relations entre les concepts est essentielle pour organiser les concepts et faire des inférences. Que la complexité des réseaux et leur utilisation diffèrent chez les experts et les novices suggère qu’une caractéristique essentielle de l’expertise est la richesse des relations faites entre les concepts. On observe en effet souvent, notamment chez les étudiants en statistiques en début de cursus, des difficultés à mettre en relation les concepts qui leur sont présentés. Il leur est par exemple difficile de percevoir les relations entre différents types de variables comme le fait que les procédures applicables aux variables nominales le sont également pour les variables ordinales et numériques et que les procédures applicables aux variables ordinales le sont également pour les variables numériques. A l’issue d’un cours de statistiques, l'étudiant ne doit pas seulement acquérir des procédures, mais également des connaissances conceptuelles sur ces procédures et les objets sur lesquels il travaille. On peut bien sûr présenter ces relations dans un cours oral ou sur papier comme on le fait [GhiglioneRichard98] dans le cours utilisé à l’Institut d’Enseignement à Distance de l’Université de Paris 8, mais notre expérience d’enseignant nous montre que les étudiants ont malgré tout des difficultés à intégrer ces relations. Dans un test que nous avons fait passer à des étudiants n’ayant eu à travailler que sur le cours papier, nous avons demandé aux étudiants de juger de la véracité de propositions comme "normaliser une distribution est une façon de transformer une distribution sur une variable ordonnée". Les résultats font apparaître un taux de réussite relativement faible et montrent une prédominance du point de vue exclusif au détriment du point de vue inclusif, autrement dit les relations d’inclusions de classe ne sont que minoritairement acquises. Nous ne détaillerons pas les résultats de cette étude qui sont en cours d’analyse, mais ce résultat souligne la nécessité d’expliciter les relations entre les concepts dans la construction d’un cursus de statistique pour psychologues.
3.1. La statistique vue comme un apprentissage procédural
Cette nécessité est plus impérative encore si on appréhende l’enseignement des statistiques à partir des données précédemment exposées et des résultats de travaux sur l’acquisition de connaissances techniques et sur l’organisation de ces connaissances. Dans le cadre de l'enseignement à distance où la transmission des connaissances méthodologiques passe pour l'essentiel par l'étude d'un cours écrit, les cours de méthodologie, comme les statistiques, peuvent être assimilés à des textes procéduraux. Il s'agit pour les étudiants à la fois d’identifier les procédures à mettre en œuvre, les contextes de mise en œuvre et les objets sur lesquels elles portent. Or de nombreuses recherches en psychologie cognitive ont montré que les textes procéduraux sont bien plus difficiles à appréhender que les textes de récits ou les textes expositifs [Chaiklin84] et notamment qu'on peut très bien en avoir une compréhension de surface sans être pour autant capable de réaliser l'action décrite par le texte [KholerAl00], [KotovskiAl85]. Considérer un cours de statistiques, non plus comme un exposé magistral d'un ensemble de connaissances que doit acquérir l'étudiant, mais comme un texte procédural, au même titre que les modes d'emploi, les consignes de résolution de problèmes, permet de donner du sens à un certain nombre de difficultés que rencontrent les étudiants. Il est ainsi fréquent d’observer l’application de procédures à des objets pour lesquels elle n’a pas de signification. Par exemple, un calcul de moyenne sur une variable nominale pour laquelle les modalités ont été codées de manière numérique (Blanc=0, Rouge=1, Bleu=2, ...). Dans un texte procédural, deux logiques de structuration des informations doivent s'articuler pour permettre une bonne compréhension [Richard02]. La première est liée aux connaissances relatives aux objets, à leurs propriétés et aux relations qu'entretiennent ces objets, c'est la logique de fonctionnement. La seconde concerne les procédures elles-mêmes, leurs conditions d'application, c'est la logique d’utilisation. Ces deux logiques renvoient à deux types de propriétés des objets : les propriétés structurales et les propriétés fonctionnelles. De ce point de vue, comprendre un texte procédural, c'est être capable "d'appréhender ces deux types de propriétés et les relier entre elles de manière à pouvoir inférer les propriétés fonctionnelles à partir des propriétés structurelles et réciproquement à expliquer les propriétés fonctionnelles par les propriétés structurelles" ([Richard02], p.20). Ces deux types de propriétés sont étroitement liés, même si en prenant un point de vue particulier, on peut toujours considérer indépendamment l'une ou l'autre de ces deux sortes de propriétés. Mais lorsqu'il s'agit d'agir, notamment dans la résolution de problèmes, il est nécessaire de les considérer conjointement [ClémentRichard97]. Ainsi appliquer des procédures à un objet, c'est lui attribuer les propriétés de la catégorie des objets qu'on traite de cette façon [PoitrenaudAl90]. Ceci a été particulièrement bien montré dans des recherches sur l'apprentissage de dispositifs techniques [TijusAl96]. Ainsi [SanderRichard97] ont montré que dans l'apprentissage de l’utilisation d'un logiciel de traitement de textes, que certains sujets novices n’utilisaient pas la touche "backspace" pour effacer un espace, lorsque celui-ci se situait à l'intérieur d'un mot. Au lieu de cela les sujets préféraient effacer les caractères situés après l'espace, puis les retapaient après avoir déplacer le curseur. Ce n'est que lorsqu'ils découvrent que l'espace peut être vu comme un caractère qu'ils utilisent spontanément la touche d'effacement. Construire un savoir-faire ne relève donc pas seulement de l'acquisition de procédures, mais également de la découverte des propriétés structurelles (un espace est une sorte de caractère) et fonctionnelles (la touche "backspace" efface également les espaces). Cette relation étroite entre propriétés de structure et propriétés liées à l'action est également confirmée par une série de travaux sur la sémantique de l'action dont les principaux résultats montrent que ces significations sont structurées par ces deux types de propriétés [Meunier99], [RichardAl01]. Pour le domaine qui nous occupe, c’est-à-dire les statistiques pour psychologues, il s’agit donc à la fois de présenter à l’étudiant la logique de fonctionnement, c’est-à-dire l’organisation des concepts sur lesquels il travaille (propriétés structurelles) et les procédures qui leur sont applicables (propriétés fonctionnelles), mais également les relations qu’entretiennent ces procédures, c’est-à-dire la logique d’utilisation.
3.2. Construction de l’ontologie.
Les travaux que nous venons d'évoquer montrent qu'au-delà de la simple présentation d'un contenu, l'enjeu principal d'un point de vue didactique est l'explicitation de la structuration des connaissances à enseigner. De notre point de vue, il paraît essentiel de développer des méthodes d'analyse de la matière de façon à expliciter la structuration des concepts qu'on cherche à enseigner et d'utiliser les ontologies ainsi construites pour faciliter l'exploration de la matière par l'étudiant. Pour cela, nous nous appuyons sur le formalisme PROCOPE développé dans notre laboratoire [Poitrenaud95], [PoitrenaudAl90]. Celui-ci a d'abord été utilisé pour décrire les procédures associées aux objets composant un dispositif. Il est fondé sur l'idée défendue par différents auteurs [Richard02] que les objets sont structurés par le contexte d'utilisation et que les procédures peuvent être vues comme des propriétés fonctionnelles des objets. En effet, il est communément admis que les propriétés structurales correspondant aux connaissances déclaratives servent de classificateurs pour les objets et la plupart des modèles de représentation des connaissances sous forme de réseaux sémantiques reposent sur ces propriétés, que celles-ci soient considérées comme définissant les catégories ou comme induisant des relations de similitude entre exemplaires, ou entre exemplaires et prototypes [SmithMedin81], [Barsalou93], [Heit97]. Les propriétés fonctionnelles, correspondant aux connaissances procédurales, ne sont, quant à elles, généralement pas considérées comme devant jouer un rôle analogue par rapport aux objets. La plupart des théories font une distinction radicale entre connaissances déclaratives et connaissances procédurales et, par conséquent, les décrivent à l’aide de formalismes différents. Pourtant, la correspondance entre les deux sortes de propriétés est manifeste : le plus souvent, c’est l’existence des parties qui autorise la fonction [TverskyHemenway84]. Par exemple, pour un oiseau, les propriétés "a des ailes" et "a des pattes" sont intimement liées aux propriétés "peut se déplacer en volant" et "peut se déplacer en marchant". En outre, l’idée que les connaissances sont structurées par les propriétés fonctionnelles a été défendue par différents auteurs [BisseretEnard69], [EnardBisseret69], [Richard83], [Bastien97]. Le réseau sémantique PROCOPE [PoitrenaudAl90], [Poitrenaud95], [Poitrenaud01] est le graphe du treillis de Galois associé aux connaissances déclaratives et procédurales sur un domaine. La notion de treillis de Galois offre un cadre unificateur pour différentes méthodes d’acquisition de concepts et de classification conceptuelle [Wille92], [GuénocheVanMechelen93], [GodinAl98], [Belohlavek00]. Dans le cas de PROCOPE, qui aborde le treillis de Galois comme un outil de modélisation cognitive [PoitrenaudAl90], [TijusAl96], [SanderRichard98], [SanderAl01], il permet d’opérer une complète intégration des connaissances déclaratives et procédurales au sein d’un formalisme unique. Formellement, un réseau PROCOPE comprend un ensemble de catégories reliées entre elles par des liens figurant la relation d’inclusion sémantique. Dans un réseau de ce type, si les objets de la catégorie X ont toutes les propriétés des objets de la catégorie Y, les X sont des sortes de Y et la catégorie des X est une sous-catégorie de la catégorie des Y. De plus, puisqu’on traite les buts et les actions comme étant les propriétés fonctionnelles des objets, il faut ajouter à la condition précédente "...et si on peut faire avec les X tout ce qu’on peut faire avec les Y". Si les X sont des Y, on dit que les X "héritent" des propriétés des Y. On peut représenter ce type de réseau par un graphe : on obtient alors ce que la théorie des graphes nomme une hiérarchie, c’est-à-dire un graphe orienté sans circuit. Notons qu’il s’agit d’une structure plus générale que celle de l’arbre : dans une hiérarchie, un nœud peut avoir plusieurs antécédents immédiats. Dans un réseau PROCOPE, une catégorie peut donc avoir plusieurs catégories superordonnées immédiates et hériter des propriétés de chacune d’entre elles. On peut dériver une hiérarchie satisfaisant les précédentes exigences à partir de la structure algébrique nommée treillis de Galois d’une relation binaire [BarbutMonjardet70]. La construction du treillis est faite à l’aide du logiciel Stone qui est l’implémentation informatique du formalisme PROCOPE [Poitrenaud01] , [PoitrenaudAlSousPresse] auquel on fournit en entrée un tableau de données décrivant les relations entre un ensemble d’objets et un ensemble de propriétés. A ce stade, propriétés structurales et fonctionnelles ne sont pas distinguées. Ce choix est motivé par l’hypothèse selon laquelle propriétés structurales et propriétés fonctionnelles, attributs physiques et savoirs sur l’action, jouent un rôle fondamentalement équivalent pour ce qui est de la catégorisation des objets. En d’autres termes, les propriétés fonctionnelles, au même titre que les propriétés structurelles, définissent un réseau sémantique, qui exprime la façon dont les objets doivent être conçus pour qu’il soit possible d’opérer efficacement sur eux. Nous l'appliquons ici à l'analyse du domaine des statistiques pour psychologues.
D’un point de vue opérationnel, la méthode consiste à dresser la liste des objets et à dresser un tableau croisant ces objets avec leurs propriétés fonctionnelles et structurelles (tableau 1). Le logiciel engendre ensuite le réseau sémantique du domaine en appliquant le principe suivant : Un objet x est une sorte d'objet y si on peut faire sur x tout ce qu'on peut faire sur y. Cette relation est en fait une relation d'inclusion. Les procédures étant vues comme des propriétés, on a une relation analogue à celle qu'on définit classiquement sur les propriétés structurelles : Un objet x est une sorte d'objet y si x a toutes les propriétés de y.

Tableau 1: L'analyse "objets-propriétés" des sortes de variables.
Cette méthode a été appliquée à l'analyse du cours de statistiques descriptives de première année de DEUG de psychologie, en prenant comme référence l'ouvrage que les étudiants de l'Institut d'enseignement à distance de l'Université de Paris 8 reçoivent [GhiglioneRichard98]. Nous ne présenterons, à titre d’illustration, que l’analyse faite sur la notion de variable. La méthode consiste à lister l’ensemble des objets et des propriétés, qu’elles soient structurelles ou fonctionnelles, puis construire la table binaire des associations objets/propriétés (tableau 1). Dans ce tableau 1, nous avons séparé les propriétés structurales (les caractéristiques des variables) et les propriétés fonctionnelles (ici les procédures applicables) pour plus de clarté.
A partir de ce tableau, le logiciel Stone met en œuvre le formalisme PROCOPE pour engendrer le réseau sémantique des objets et des procédures. Concrètement, le logiciel permet de construire des catégories en regroupant les objets partageant les mêmes propriétés et de structurer ces catégories par des relations d'inclusion de classes.
Figure 7 : Réseau sémantique de la notion de variable.
On voit dans le réseau sémantique de la Figure 7que la notion de variable n'est pas une notion simple. Elle se subdivise en deux sous catégories en fonction du statut de la variable (Facteur versus Variable Dépendante). La notion de variable observée ou VD est ensuite structurée par le type d'échelle de mesure. Bien évidemment, une telle organisation des connaissances reflète un point de vue particulier sur ces objets, celui d’un expert et ce point de vue n’est souvent pas trivial pour l’étudiant. Ainsi, il arrive fréquemment qu’une variable soit contrôlée a posteriori (comparaison de groupes d’âge ou de sexe). Au sens propre on peut dès lors considérer que c’est une variable observée, mais le fait de la contrôler, même a posteriori, lui fait prendre un statut particulier qui fait que les procédures applicables ne dépendent plus de sa structure, sauf dans le cas de la régression linéaire, méthode qui n’est pas au programme du cours et qui est ignorée dans cette analyse. C’est alors la structure de la variable dépendante qui détermine les méthodes d’analyse applicables.
Figure 8 : Réseau sémantique des procédures applicables aux variables
Ces propriétés structurelles sont corrélées avec les propriétés fonctionnelles et on peut également regarder ces objets à travers les relations qu'entretiennent les procédures. Sur ces objets, on ne peut que recoder les variables (Figure 8). Il existe deux types de recodage : le regroupement de modalités et la transformation de variable (transformation mathématique). Cette dernière n'est applicable qu'aux variables numériques. Le regroupement de modalités est en revanche applicable à tous les types de variables, mais diffère en fonction de l'échelle de mesure (regroupement sémantique, par proximité ou en classes). Ces deux réseaux sémantiques représentent les deux points de vue selon lesquels on peut structurer le cours de statistiques descriptives : les objets (logique de fonctionnement) et les buts qu'on a sur ces objets (logique d’utilisation). Ils permettent aux étudiants de prendre conscience de l'existence de ces deux points de vue et de les explorer pour identifier les filiations de propriétés qui conduisent à une telle structuration.
4. Réalisation et navigation dans l’EIAH
L’environnement pédagogique des étudiants, pour ce cours, est constitué d’un cours sur papier édité chez Dunod [GhiglioneRichard98], d’un fascicule d’exercices et de devoirs (type problèmes à résoudre) à envoyer à l’enseignant pour correction. Les étudiants disposent également de moyens de communication avec l’enseignant (courrier, mail, forum, foire aux questions et permanences téléphoniques hebdomadaires) et sont ainsi accompagnés de manière individualisée dans l’étude de leur cours. Des travaux dirigés, en présentiel à l’Institut, sont également au programme de la deuxième année de DEUG. Dans ce contexte, les aides pédagogiques en ligne que nous évoquons dans cet article constituent une aide à la compréhension du cours et non le cours lui-même. Il est supposé (mais l’étudiant n’y est nullement contraint) que le cours est étudié préalablement à l’utilisation des aides pédagogiques en lignes que nous situons comme des outils de révision et d’approfondissement du cours.
L’environnement informatique d’apprentissage fondé sur les principes que nous venons de présenter est en cours de réalisation. Nous en présenterons donc les principes généraux et une maquette permettant de se faire une idée plus précise du projet.
4.1. L’interface informatique.
L’interface informatique prévoit une interface d’édition destinée à l’enseignant et une interface d’utilisation pour l’étudiant.
Côté enseignant, l’interface permet de déclarer les concepts et les relations entre les concepts et d’associer les concepts à un ou plusieurs matériels didactiques (textes, diaporama, quiz, etc). L’interface permet également d’introduire un ordre dans la consultation des séquences s’il y a lieu (travailler la séquence sur la moyenne avant celle sur l’écart-type par exemple). Elle calcule ensuite le réseau sémantique à afficher sur l’interface de l’étudiant. Cette interface permet donc une gestion simple par l’enseignant de l’interface de navigation de l’étudiant et permet également d’envisager l’application de cette approche pour d’autres cours (notamment les cours de statistiques de deuxième année de DEUG et de Licence). Cette interface suppose bien-sûr que le travail de structuration des concepts et de séquençage du cours ait été fait en amont, ainsi que la préparation des séquences. Pour ce qui concerne le cours de statistique, nous avons ainsi découpé le cours en 29 séquences correspondant aux procédures que l’étudiant doit acquérir. A chacune de ces séquences, sont associés un texte court rappelant les définitions des notions en jeu et les propriétés de la catégorie d’objets sur lesquels l’étudiant travaille, un diaporama présentant la procédure et son application et un quiz permettant de tester la compréhension des concepts mis en œuvre et l’application de la procédure.
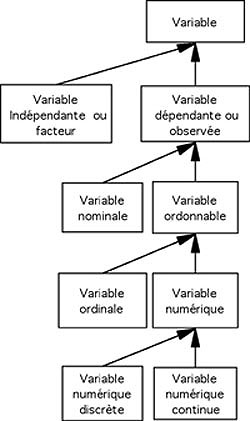
Coté étudiant, l’interface se présente pour ce cours sous la forme de deux réseaux sémantiques dans lequel il pourra naviguer. Le premier réseau est celui des objets statistiques. La Figure 9reproduit une copie d’écran de la maquette.
Figure 9 : Le réseau sémantique des objets statistiques
Ce réseau sémantique est une ontologie partielle du domaine des statistiques pour psychologues. Les nœuds représentent les concepts et le réseau est structuré hiérarchiquement par une relation d’inclusion (est une sorte de). Il correspond à la hiérarchie des catégories d’objets sur lesquels on peut appliquer des procédures d’analyse. Il ne prétend pas à l’exhaustivité (d’autres objets statistiques existent) mais vise à rendre compte des relations qui apparaissent importantes du point de vue de l’enseignant, compte tenu de ses choix pédagogiques, et destiné à être mis en avant dans le cours, en l’occurrence les statistiques destinées à des étudiants de DEUG première année. Son utilisation est relativement simple, le survol d’un des nœuds du réseau permet d’afficher le menu contextuel présentant la liste des séquences de cours associées. Ce menu correspond à la liste des propriétés fonctionnelles c’est-à-dire des procédures applicables à l’objet en question. Par exemple, le survol du nœud "variable nominale" permet d’accéder à la séquence sur le recodage sémantique. De la même façon, le survol du nœud "variable ordinale" donne accès à la séquence de cours sur le regroupement par proximité et en survolant le nœud "variable numérique", on pourra consulter les séquences sur le regroupement en classes et la transformation de variable. L’étudiant voit également s’afficher dans la barre d’état du navigateur une courte définition de la notion survolée. Lorsque l’étudiant sélectionne une des options dans le menu contextuel associé à une des notions, une fenêtre de type pop-up s’ouvre pour présenter les différents objets pédagogiques associés (textes, diaporamas, quiz).
Dans la Figure 9, on peut voir également deux boutons en haut à droite de l’interface : aide et procédures. Le bouton "aide" permet d’accéder à un aide technique concernant l’utilisation de l’interface. Le bouton "procédures" donne accès à la structuration des procédures du point de vue des buts. Cette seconde interface est présentée Figure 10.
Figure 10 : le réseau sémantique des procédures
Dans ce réseau, les nœuds ne sont pas des concepts, mais des propriétés (rappelons que nous considérons les procédures comme des propriétés fonctionnelles des objets statistiques) et les principes de construction et d’utilisation sont similaires au réseau précédent. Ce réseau donne à voir à l’étudiant les relations qui existent entre les procédures statistiques qui sont également hiérarchisées par une relation d’inclusion, mais cette relation doit dans ce cas être interprétée comme "est une façon de". Le survol et la sélection du nœud correspondant à une procédure permettent d’accéder aux objets pédagogiques associés et ainsi d’étudier cette procédure.
5. Discussion et perspectives.
Les deux réseaux sémantiques qui viennent d’être présentés constituent deux espaces de navigation pour l’étudiant dans le cours. Ils visent à expliciter la coexistence de deux points de vue sur le domaine des statistiques et à engager l’étudiant dans une articulation de ces deux points de vue que constituent la structuration rationnelle des concepts et la structuration fonctionnelle des procédures. Nous soutenons en effet que la compréhension des relations entre les concepts fait souvent défaut et est largement à l’origine des difficultés rencontrées lors de la mise en œuvre des connaissances. Le champ des domaines de connaissances pour lequel il est fructueux de travailler selon cette démarche reste à délimiter. Les premières tentatives tendent à indiquer que sont en premier lieu visés les domaines dans lesquels les concepts peuvent être décrits en intension par une liste de traits, ce qui est notamment le cas des domaines faisant l’objet de descriptions formelles tels que les mathématiques ; ou les domaines dans lesquelles les dimensions procédurales sont centrales, ce qui est notamment le cas des dispositifs techniques.
Nous ne souscrivons pas à l’affirmation que la simple navigation dans un ou plusieurs réseaux sémantiques soit une aide pédagogique suffisante. Comme n’importe quel cours, et quelle que soit la forme qui lui est donnée, il s’agit de la mise à disposition de l’étudiant du rapport que l’enseignant entretient avec le savoir qu’il cherche à transmettre. Les réseaux sémantiques ne sont pas forcément triviaux d’emblée et n’ont pas nécessairement vocation à l’être. Ils sont un moyen pour l’enseignant d’expliciter la structuration de connaissances et d’engager l’étudiant dans la reconstruction de ces relations, relations qui seront essentielles dans la future utilisation des connaissances qu’il vient d’acquérir. L’interface va donc le conduire à s’interroger (pourquoi l’enseignant ne met-il pas les variables indépendantes avec les variables observées alors qu’on peut contrôler une variable a posteriori ?). L’explicitation des réseaux sémantiques peut constituer une aide à l’apprentissage dans le sens où elle donne à voir et à comprendre qu’au-delà des concepts et des procédures, la structuration des connaissances est une composante importante pour maîtriser son sujet.
Dans leur forme actuelle, les réseaux présentent une complexité importante. Il serait intéressant de la réduire et si possible de l’adapter au niveau d’acquisition de l’étudiant. Cette idée attirante, quoique difficile à mettre en œuvre en pratique, pourrait consister à présenter tout ou partie des concepts sous la forme d’un réseau sémantique correspondant au niveau de l’apprenant et de le faire tendre vers le réseau de l’expert-enseignant au fur et à mesure de sa progression dans le cours. Cette démarche demande le développement d’outils de diagnostic. Nous disposons bien sûr de méthodes pour identifier la structuration des connaissances d’un sujet sur un domaine particulier (les travaux sur la catégorisation et le formalisme PROCOPE en font partie), qui devront être adaptées à ce contenu disciplinaire et au cadre de cours en ligne pour l’adapter au contexte de l’enseignement à distance via le Web. Ce défi difficile vaut la peine d’être relevé car il ouvre la perspective d’une progression individualisée au sein de l’EIAH.
Une question plus théorique associée concerne les mécanismes d’apprentissage eux-mêmes. De notre point de vue, apprendre consiste à acquérir des concepts (et des procédures quand il y a lieu) mais aussi à les structurer correctement (c’est-à-dire conformément à la structuration d’un expert-enseignant). Ce point de vue n’est pas très original et finalement assez partagé dans le domaine de la psychologie. Cependant, sauf peut-être dans des domaines très particuliers, on connaît encore mal les conditions d’acquisition d’un nouveau concept et d’intégration aux connaissances antérieures, pas plus que ne sont claires les conditions dans lesquelles un sujet est conduit à restructurer ces connaissances. Cela n’est, bien entendu, pas sans lien avec l’utilisation des connaissances et les conditions dans lesquelles elles peuvent être réinvesties voir généralisées. Ainsi, on pourrait être surpris de voir des étudiants se débattre avec l’inférence statistique alors qu’elle est essentiellement une généralisation de la procédure consistant à situer un individu dans une distribution et que c’est bien comme cela que qu’on présente l’inférence statistique dans leur cours. Manifestement, le saut conceptuel consistant à voir un résumé statistique comme une observation et un protocole comme un individu statistique à situer dans un ensemble de protocoles possibles est très difficile à faire. Comment favoriser le changement de point de vue ? Dans quelles conditions peut-il avoir lieu ? Au-delà du problème pédagogique particulier lié à ce cours de statistiques, ce sont donc bien les conditions d’acquisition et d’utilisation de connaissances structurées qui sont ici interrogées.
Références
Références bibliographiques
Adelson, B. (1981). Problem solving and the development of abstract categories in programming languages. Memory & Cognition (9), 422-433.
Anderson, J. R. (1991). The adaptive nature of human categorization, Psychological Review (98) 409-429.
Barbut M., Monjardet, B. (1970). Ordre et classification, Algèbre et combinatoire, Tome 2, Paris: Hachette.
Barsalou, L.W. (1983). Ad hoc categories. Memory and Cognition (11), 211-227.
Barsalou, L.W. (1993). Challenging assumptions about concepts. Cognitive Development (8), 169-180.
Bassok, M. (2001). Semantic alignments in mathematical word problems. In Gentner, D., Holyoak, K. J., & Kokinov, B. N. (Eds.) The analogical mind: Perspectives from cognitive science. Cambridge, MA: MIT Press.
Bassok, M., Wu, L.L., & Olseth, K.L. (1995). Judging a book by its cover: Interpretative effects of content on problem-solving transfer. Memory and Cognition (23), 354-367.
Bassok, M., & Olseth, K.L. (1995). Object-based representations: Transfer between cases of continuous and discrete models of change. Journal of Experimental Psychology: Learning, Memory and Cognition (21), 1522-1538.
Bastien, C. (1997). Les connaissances de l’enfant à l’adulte. Paris : Colin.
Belohlavek, R. (2000). Fuzzy Galois connections and fuzzy concept lattices: From binary relations to conceptual structures. In: Novak V., Perfileva I. (eds.): Discovering the World with Fuzzy Logic. Physica-Verlag (Springer-Verlag Company), pp. 462-494, Heidelberg, New York.
Bisseret, A. Enard, C. (1969). Le problème de la structuration de l’apprentissage d’un travail complexe. Bulletin de Psychologie (23), 632-648.
Blessing, S.B., & Ross, B.H. (1996). Content effects in problem categorization and problem solving. Journal of Experimental Psychology: Learning, Memory & Cognition (22), 792-810.
Bower, G.H., Clark, M.C., Lesgold, A.M., & Winzenz, D. (1969). Hierarchical retrieval schemes in recall of categorized word lists. Journal of Verbal Learning and Verbal Behavior (8), 323-343.
Chaiklin, S. (1984). On the nature of verbal rules and their role in problem solving. Cognitive Science, 8, 131-155.
Chi, M.T.H., Feltovitch, P.J., & Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121-152.
Chi, M.T.H., Glaser, R. & Rees, E. (1982). Expertise in problem solving. In R.J. Sternberg (Ed.), Advances in the psychology of human intelligence (pp. 7-75). Hillsdale, NJ: Erlbaum.
Chi, M.T.H., Bassok , M., Lewis, M.W., Reimann, P., & Glaser, R. (1989). Self-explanations: How students study and use examples in learning to solve problems. Cognitive Science (13), 145-182.
Chi, M.T.H., & VanLehn, K. (1991). The content of physics self-explanations. Journal of the Learning Sciences (1), 69-106.
Clément, E., Richard, J. F. (1997). Knowledge of domain effects in problem representation: the case of Tower of Hanoi isomorphs. Thinking and Reasoning, 3, 133-157.
Collins, A.M., & Loftus, E.F. (1975). A spreading-activation theory of semantic processing. Psychological Review (82), 407-428.
Cordier, F. (1993). Les représentations cognitives privilégiées: Typicalité et niveau de base. Lille: Presses Universitaires de Lille.
Enard, C., Bisseret, A. (1969). L’utilisation de l’enseignement programmé dans la construction de la mémoire permanente chez l’opérateur humain. In La recherche en enseignement programmé. Paris : Dunod
Ghiglione, R., Richard, J. F. (1998)., Cours de psychologie: Bases, méthodes et épistémologie, Vol. 2, Paris : Dunod,.
Glucksberg, S., & Keysar, B. (1990). Understanding metaphorical comparisons: beyond similarity. Psychological Review (97), 3-18.
Godin, R., Mili, H., Mineau, G. W., Missaoui, R., Arfi, A. & Chau, T.-T. (1998). Design of Class Hierarchies based on Concept (Galois) Lattices. Theory and Application of Object Systems (TAPOS), 4(2), 117-134.
Guénoche, A., & Van Mechelen, I. (1993). Galois approach to the induction of concepts. In I. Van Mechelen, J. Hampton, R.S. Michalski, & P. Theuns (Eds.)
Hardiman, P.T., Dufresne, R, & Mestre, J.P. (1989). The relation between problem categorization and problem solving among experts and novices. Memory & Cognition (17), 627-638.
Heit, E. (1997). Knowledge and concept learning. In K. Lamberts and D. Shanks (Eds.), Knowledge, concepts and categories (pp. 7-41). London: UCL Press.
Hofstadter, D. (1997). Le ton beau de Marot: In praise of the music of language. New York: Basic Books.
Holyoak, K. J. (1985). The pragmatics of analogical transfer. In G.H. Bower (Ed.), The Psychology of Learning and Motivation, Vol 19, (pp. 59-87). New York: Academic Press.
Holyoak, K. J., & Koh, K. (1987). Surface and structural similarity in analogical transfer. Memory and Cognition (15), 332-340.
Johnson, K. E., & Mervis, C. B. (1997). Effects of varying levels of expertise on the basic level of categorization. Journal of Experimental Psychology : General (126), 248-277.
Kholer, C., Kekenbosch, C., Verstigel, J. C. (2000). La compréhension d'un texte procédural: un processus à profondeur variable. International Journal of Psychology (35) 258-269.
Kotovsky, K., Hayes, J. R., Simon, H. A. (1985). Why are some problem hard ? Evidence from tower of Hanoi. Cognitive Psychology (17), 248-294.
Medin, D. L., Lynch, E. B., & Solomon, K. O. (2000). Are there kinds of concepts? Annual Review of Psychology (51), 121-147.
Meunier, J. M. (1999). Les primitives sémantiques et l'organisation des significations d'action, Thèse de doctoratUniversité Paris 8.
Murphy, G. L., & Ross, B. H. (1994). Prediction from uncertain categorizations. Cognitive Psychology (27), 148-193.
Poitrenaud, S. (2001). Complexité cognitive des interactions homme-machine. Paris : L’Harmattan
Poitrenaud, S. (1995). The PROCOPE semantic network : an alternative to actions grammars. International Journal of Human-Computer Studies (42), 31-69.
Poitrenaud, S., Richard, J-F., & Tijus, C.A. (1990). An object-oriented semantic description of procedures for evaluation of interfaces. 5th European Conference on Cognitive Ergonomics. Urbino.
Poitrenaud, S., Richard, J-F., Tijus, C. Properties, Categories and Categorization. Accepté par la revue Thinking and Reasonning
Politzer, G. (1991). L’informativité des énoncés: Contraintes sur le jugement et le raisonnement. Intellectica (11), 111-147.
Puff, C.R. (1970). Role of clustering in free recall. Journal of Experimental Psychology (86), 384-386.
Reed, S.K. (1987). A structure mapping model for word problems. Journal of Experimental Psychology: Learning Memory and Cognition (13), 124-139.
Richard, J.F. (2002). Compréhension de textes procéduraux et catégorisation. Psychologie Française (47), 19-32.
Richard J.F. (1983). Logique de fonctionnement et logique d'utilisation. Rapport de recherche INRIA, n° 202, 51 p.
Richard J.F. , Meunier J.M., Poitrenaud S. (2001). Propositions pour une description sémantique des énoncés d’action. Psychologie sociale de la communication, Colloque en hommage à Rodolphe Ghiglione, 2-3 Février 2001, Université de Paris 8, Saint-Denis.
Richard, J.-F., & Sander, E. (2000). Activités d’interprétation et de recherche de solution dans la résolution de problèmes. In J-N. Foulin & C. Ponce (Eds.), Lire, écrire, compter, apprendre : Les apports de la psychologie des apprentissages, pp. 91-102. Editions du CRDP de Bordeaux.
Rosch, E. (1978). Principles of categorization. In E. Rosch and B.B. Lloyd (Eds.), Cognition and categorization (pp. 27-48). Hillsdale, NJ: Erlbaum.
Rosch, E., Mervis, C.B., Gray, W. D., Johnson, D. M., & Boyes-Braem, P. (1976). Basic objects in natural categories. Cognitive Psychology (8), 382-439.
Sander, E. (2000). L’analogie, du Naïf au Créatif : analogie et catégorisation. Paris, L’Harmattan
Sander, E. (2003). Analogie et catégorisation. In K. Duvignau, O. Gasquet & B. Gaume (éds.). Regards croisés sur l’analogie. Revue d’Intelligence Artificielle, Hermès Sciences, (5-6), 719-732
Sander, E., Poitrenaud, S., Fresneau, J, & Tapol, S. (2001). Econf : Test utilisateurs et analyse fonctionnelle. Rapport de Recherche FT R&D.
Sander, E., Poitrenaud, S., Bastide, A. (2002). Le marquage : relation entre niveau d'abstraction et type de catégorisation. Colloque les apprentissage et leurs dysfonctionnements. 17 Juin 2002. Paris
Sander, E., & Richard, J.-F. (1997). Analogical transfer as guided by an abstraction process: the case of learning by doing text editing. Journal of Experimental Psychology: Learning, Memory and Cognition (23), 1459-1483.
Sander, E., & Richard, J-F. (1998). Analogy making as a categorization and an abstraction process. In K. Holyoak, D. Gentner, & B. Kokinov (Eds.) Advances in analogy research: Integration of theory and data from the cognitive, computational and neural sciences (pp. 381-389). Sofia: NBU Series in Cognitive Sciences
Schoenfeld, A.H., & Herrmann, D.J. (1982). Problem perception and knowledge structure in expert and novice mathematical problem solvers. Journal of Experimental Psychology: Learning, Memory and Cognition (8), 484-494.
Silver, E.A. (1979). Student perceptions of relatedness among mathematical verbal problems. Journal for Research in Mathematics Education (10), 195-210.
Silver, E.A. (1981). Recall of mathematical problem information: solving related problems. Journal of Research in Mathematical Education (12), 54-64.
Smith, E.E., & Medin, D.L. (1981). Categories and concepts. Cambridge: Harvard University Press.
Tanaka, J.W., & Taylor, M. (1991). Object categories and expertise: Is the basic level in the eye of the beholder? Cognitive Psychology (23), 457-482.
Tijus, C.A. (1996). Assignation de signification et construction de la représentation. Manuscrit d’habilitation à diriger des recherches, Université Paris VIII.
Tijus, C., Richard, J. F., Leproux, C. (1996). Une méthode de pronostic des erreurs et des incidents pour la conception de dispositifs. Le travail humain (59), 335-376.
Tversky, B., & Hemenway, K. (1984). Objects, parts, and categories. Journal of Experimental Psycholgy: General (113), 171-191.
Tversky, B., & Hemenway, K. (1991). Parts and the basic level in the natural categories and artificial stimulies: Comments on Murphy (1991). Memory & Cognition (19), 439-442.
Vosniadou, S. (1989). Analogical reasoning as a mechanism in knowledge acquisition: a developmental perspective. In S. Vosniadou & A. Ortony (Eds.), Similarity and analogical reasoning (pp. 413-437). Cambridge: Cambridge University Press.
Wille, R., (1992). Concept lattices and conceptual knowledge systems. Comput. Math. Appl (23), 493-515.
 A
propos des auteurs
A
propos des auteurs
Emmanuel SANDER est maître de conférences en psychologie cognitive à l’université Paris 8 et membre du laboratoire Cognition et Usages. Ses recherches portent sur le rôle des connaissances antérieures sur la compréhension, la résolution de problèmes et l’apprentissage, avec des applications dans le domaine des apprentissages scolaires et en ergonomie cognitive des interfaces.
Adresse : Laboratoire Cognition et Usages Département de Psychologie. Université Paris 8. 2 Rue de la Liberté. 93526 Saint-Denis Cedex 02, France
Courriel : sander@univ-paris8.fr
Jean-Marc MEUNIER est maître de conférences à l’Institut d’Enseignement à Distance de l’Université de Paris 8. Responsable du DEUG, il enseigne la psychologie cognitive et les statistiques aux étudiants de DEUG et de Licence. Ses thèmes de recherches sont la sémantique de l’action et des états mentaux abordés notamment sous l’angle de la structuration des connaissances. Il s’intéresse également au rôle et à la variablité de la structuration des connaissances dans le partage des connaissances.
Adresse : Laboratoire Cognition et Usages Département de Psychologie. Université Paris 8. 2 Rue de la Liberté. 93526 Saint-Denis Cedex 02, France
Courriel : jmeunier@univ-paris8.fr
Christelle BOSC-MINÉ finalise actuellement une thèse de doctorat sur la résolution de problèmes nécessitant un raisonnement hypothético-déductif. Elle est chargée du cours de Statistiques Descriptives pour Psychologues à l’IED-Paris 8 (Institut d’Enseignement à Distance) et travaille au sein du Laboratoire Cognition et Usages de l’Université Paris 8 sur un projet d’aide à l’apprentissage par l’acquisition de relations conceptuelles, dans le domaine des statistiques pour psychologues.
Adresse : Laboratoire Cognition et Usages Département de Psychologie. Université Paris 8. 2 Rue de la Liberté. 93526 Saint-Denis Cedex 02, France
Courriel : christelle.bosc-mine@iedparis8.net
![]()
Référence de l'article :
Emmanuel SANDER, Jean-Marc MEUNIER, Christelle BOSC-MINÉ, Approche ontologique et navigation dans un E.I.A.H Le cas de l’enseignement des statistiques, Revue STICEF, Volume 11, 2004, ISSN : 1764-7223, mis en ligne le 30/12/2004, http://sticef.org