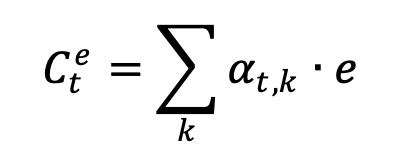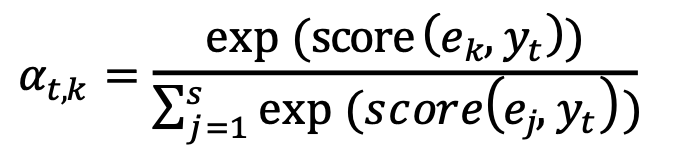Sommaire

Rechercher

• auteur
• année
• titre
• résumé
• abstract
• rubrique

Contact : infos@sticef.org

Une approche hybride à la modélisation de l’apprenant dans un STI pour l’apprentissage du raisonnement logique

Roger NKAMBOU, Ange TATO (CRIA, Université du Québec à Montréal), Janie BRISSON, Serge ROBERT (LANCI, Université du Québec à Montréal), Maxime SAINTE-MARIE (Aarhus, Université du Danemark)

	RÉSUMÉ : Cet article présente une démarche hybride pour la modélisation de l’apprenant dans le STI MUSE-Logique conçu pour l’apprentissage du raisonnement logique. Un réseau bayésien à validation experte est d’abord proposé, suivi par un modèle construit à partir des données qui permet d’améliorer la structure du réseau bayésien et son initialisation pour un nouvel apprenant. Un autre modèle construit par apprentissage profond sur des données, complète la solution hybride proposée. La combinaison de ces trois méthodes confère au modèle apprenant une validité induite des connaissances expertes et des données, et améliore son pouvoir prédictif. MOTS CLÉS : Modèle apprenant, Diagnostic/traçage de connaissances.
A hybrid approach to learner modeling in an intelligent tutoring system for logical reasoning learning
	ABSTRACT : This paper presents a hybrid approach to learner modeling into MUSE-Logic, an ITS for logical reasoning learning. A Bayesian network built by experts is first proposed, followed by a model built from data that improves both the Bayesian network structure and its initialization for a new learner. A second model built from deep learning on data, completes the proposed hybrid solution. The combination of these three methods gives the learner model both expert and data validity, and significantly improves its predictive power. KEYWORDS : Student model, Cognitive Diagnosis, Knowledge Tracing.

• 1. Introduction
• 2. Cadre théorique
• 3. Conception participative du module expert
• 4. Le modèle de l’apprenant
• 5. Le module Tuteur de Muse-Logique
• 6. Conclusion
• RÉFÉRENCES
• ANNEXE

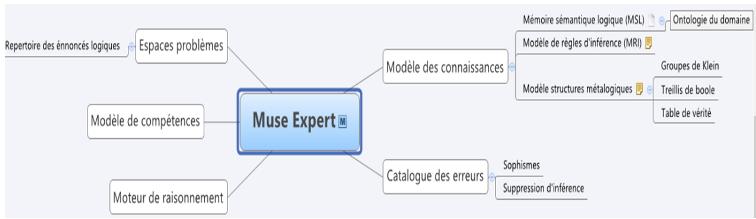
1. Introduction

De nombreuses expériences en sciences cognitives montrent que des erreurs systématiques sont courantes chez l’humain dans l’usage du raisonnement logique (Girotto et al., 1989), (Rossi et van der Henst, 2007). Un certain nombre de questions se posent lors de la recherche de solutions pour améliorer les compétences humaines dans ce domaine : quels sont les phénomènes impliqués dans l'acquisition de compétences de raisonnement logique ? Peut-on éliciter ces compétences ainsi que les connaissances sous-jacentes ? Quelles sont les stratégies d'adaptation pour favoriser le développement de la compétence logique ? Quelles sont les caractéristiques d'un système de tutorat intelligent (STI) pour soutenir cet apprentissage ? Les réponses à ces questions ne peuvent être apportées sans une explication et une compréhension appropriée des connaissances sous-tendant le raisonnement logique et les erreurs commises par les humains, couplées avec la participation active d'experts, notamment des logiciens, des psychologues du raisonnement et des professionnels de l'éducation en logique.

Le projet Muse-Logique regroupe des chercheurs dans une équipe multidisciplinaire mise en place en 2013. L'objectif est d'étudier les bases de l'acquisition des compétences de raisonnement logique, de comprendre les difficultés liées à cet apprentissage et de créer un STI capable de détecter, de diagnostiquer et de corriger les erreurs de raisonnement dans diverses situations. Pour ce faire, notre approche de conception participative vise à :

- fournir un catalogue des erreurs de raisonnement logique ;

- développer une théorie originale des causes de ces erreurs, y compris une théorie de la compétence en raisonnement logique ;

- analyser les structures formelles du traitement de l’information que l’on trouve dans les systèmes logiques ;

- développer un système de tutorat intelligent pour aider les apprenants à améliorer leurs capacités de raisonnement ;

- ultimement, aider les experts à redéfinir la nature de la rationalité humaine en utilisant les STI comme un banc d'essai pour tester d'autres hypothèses de la science cognitive du raisonnement.

L’approche participative adoptée a mené à l’élaboration de composants essentiels pour la construction du STI Muse-Logique. Ceux-ci ont été préalablement élicités, validés et argumentés par les experts. Ces composants incluent le catalogue des erreurs, les structures et méta-structures du raisonnement logique et les stratégies remédiatives favorisant l’émergence de bons modèles mentaux. Muse-Logique dans sa version actuelle implémente ces composants pour la logique classique des propositions et offre une panoplie d’activités permettant à un apprenant de développer sa compétence du raisonnement logique dans plusieurs classes de situations que nous avons établies avec les experts : concrètes, contrefactuelles et abstraites.

Cet article décrit la démarche de conception participative de Muse-Logique, notamment les fonctionnalités des trois modules issus de celle-ci. La section 2 décrit les fondements théoriques sous-jacents à Muse-Logique, suivie par les sections 3 et 4 qui décrivent les résultats de la conception participative des trois principaux composants du système : le modèle du domaine, le modèle de l’apprenant et le tuteur. Une attention particulière est accordée à l’approche hybride de la modélisation de l’apprenant, approche qui allie réseau bayésien, modèle de diagnostic cognitif et apprentissage profond pour offrir un modèle apprenant doté d’un meilleur pouvoir prédictif. La section 5 illustre l’implémentation de Muse-Logique, elle est suivie d’une conclusion qui résume les contributions et quelques travaux futurs.

2. Cadre théorique

Pourquoi construire un système pour le raisonnement logique ? Cette idée part de différents constats listés ci-dessous.

- Une partie importante de la connaissance humaine relève du traitement de l’information par des raisonnements (Markovits, 2014).

- Le raisonnement logique occupe une place importante dans la cognition (Evans, 2002).

- Le raisonnement logique humain est plus souvent fondé sur les logiques non-classiques (comme les logiques intuitionnistes) que classiques (Robert, 2005).

- En tant que machine cognitive en situation de lutte pour sa survie, l’humain tend à faire des erreurs systématiques dans ses raisonnements logiques (Evans, 2002), (Evans et al., 1993).

- Ces erreurs peuvent être dues à l’emploi de stratégies de découverte (inductives, analogiques, abductives) dans un contexte de justification.

- Apprendre à raisonner logiquement, c’est apprendre comment fonctionne le traitement cognitif de l’information, tout en apprenant les lois et procédures valides du raisonnement logique (Robert, 2005).

- Les mécanismes cognitifs du raisonnement humain (Mercier et al., 2017) sont le produit de modules cérébraux relativement autonomes, mais également en interaction étroite entre eux.

À partir de ces postulats dérivant de la littérature en psychologie du raisonnement, l'objectif de nos travaux a consisté à rassembler les développements récents dans les domaines des systèmes tutoriels intelligents, des sciences cognitives et de l’intelligence artificielle pour proposer un environnement d’apprentissage capable d’aider les étudiants à améliorer leurs compétences en logique. Notre perspective pour étudier le raisonnement logique est :

- naturaliste, les mécanismes du raisonnement sont le résultat d’une histoire évolutionnaire qui peut être expliquée (Dennett, 2003) ;

- cognitiviste, la cognition est du traitement d’information ;

- méliorativiste, la compréhension des normes logiques peut nous aider à améliorer nos compétences en raisonnement logique.

Dans ce contexte, l’information est définie comme de la régularité, par opposition à la probabilité. Le raisonnement consiste à tirer de l’information (conclusion), à partir d’informations données (prémisses), en appliquant une règle (implicite ou explicite). Le type de règle définit la nature du raisonnement. Quand ces règles de raisonnement sont logiques, elles sont non ampliatives, c’est-à-dire qu’elles n’augmentent pas l’information entre les prémisses et la conclusion, par opposition aux raisonnements créatifs, qui sont ampliatifs. Ainsi, notre hypothèse sur l’erreur logique est que lorsqu’elle est syntaxique, elle vient du traitement du raisonnement logique comme s’il s’agissait d’un raisonnement créatif. C’est le cas des sophismes (un des deux types d’erreurs de raisonnement que nous traitons dans ce travail). Les sophismes sont en effet des inférences qui créent de l’information sans justification pour le faire (Robert, 2005). Les erreurs surviennent aussi lorsque les contenus alternatifs ne sont pas considérés. Le deuxième type d’erreur que nous traitons dans nos travaux est connu comme étant « la suppression d’inférence » (Espino et Byrne, 2020). Nous exploitons des théories liées à ces deux types d’erreurs pour offrir un cadre d’apprentissage du raisonnement logique capable de tracer ces erreurs et d’aider l’apprenant à les inhiber. Par exemple, des études ont prouvé que la sensibilité aux contre-exemples était un excellent moyen d’inhiber les sophismes de l’implication (Markovits et al., 2013).

Les STI ont fait avancer la compréhension de l’apprentissage en général, mais ont aussi fait leurs preuves quant à leur capacité à soutenir l’apprentissage du raisonnement en sciences, mathématiques, et même en logique (Barnes et Stamper, 2010), (Lesta et Yacef, 2002), (Tchetagni et al., 2007). Nous pouvons formuler deux limites des STI proposés en logique. D’abord, ces systèmes ne se fondent pas sur une élicitation des connaissances et des structures logiques essentielles au raisonnement, limitant ainsi leur portée explicative du raisonnement de l’apprenant. Ensuite, ils ne se fondent pas sur des théories fondamentales de l’erreur de raisonnement au centre desquelles se trouve la théorie des processus duaux (Evans et al., 1993), (Stanovich, 2011). Celle-ci identifie deux types de processus de raisonnement qui peuvent être activés dans le raisonnement logique : des processus de type 1, spontanés, automatiques, inconscients, peu coûteux sur le plan des ressources cognitives et probablement innés, et des processus de type 2, réfléchis, récents, contrôlés, et qui font appel aux ressources cognitives telle la mémoire de travail. Les processus de type 1 nous permettent de faire certains raisonnements logiquement valides, mais ils sont aussi responsables de plusieurs erreurs. Ces processus de type 1 ne peuvent pas être éliminés, ils sont trop ancrés en nous, mais nous pouvons apprendre à les inhiber et à activer des processus de type 2. Cette activation accroît considérablement notre compétence logique en nous permettant d’éviter les erreurs causées par les processus de type 1. Nous appuyant sur ces thèses, nous explorons les différences entre ces deux types de processus et les stratégies pour inhiber les premiers et activer les seconds. Cette perspective s’arrime avec la théorie de l’inhibition cognitive de Houdé, qui indique l’importance d’apprendre à inhiber les automatismes acquis (qui s’exercent grâce au système 1, si on fait un parallèle avec la théorie des processus duaux). Ces automatismes acquis constituent la source de plusieurs erreurs de raisonnement tant chez l’enfant que chez l’adulte (Houdé, 2000), (Houdé, 2019).

L’activation des processus de type 2 et la correction de l’erreur logique ne peuvent se faire sans l’inhibition des processus de type 1 et cette inhibition exige de prendre conscience de l’erreur. En voulant améliorer la théorie du développement cognitif de Piaget, Moshman (Moshman, 2004) a démontré qu’une prise de distance métacognitive est essentielle à cette prise de conscience de l’erreur et à son inhibition. Notre projet explore cette thèse et tente de montrer comment des détours métacognitifs sont essentiels à l’acquisition de la compétence logique. Ainsi, lorsque plongée dans différents contextes, mais avec un même problème soumis, une personne éprouverait de la difficulté à bien conclure, même dans une logique apparemment simple comme la logique des propositions, elle pourrait réussir dans un contexte plus commun qu’un contexte plus abstrait. Le contexte ici renvoie à la manière dont est formulé le problème. Il peut être familier (causal), contrefactuel ou encore abstrait. Les théories évolutionnistes ont pu faire ressortir l’influence des biais et des heuristiques liés aux effets de contexte. Ces théories soutiennent que même si nous avons la technique logique appropriée pour raisonner, certains facteurs tels que les biais de croyance et les heuristiques avec lesquels nous évoluons toute notre vie influenceront notre raisonnement (Cosmides, 1989), (Varin, 2007). Grâce à ces théories, il devient possible d’expliquer certains raisonnements invalides.

Selon Robert, le processus d’opérations mentales met en relation le raisonnement et la catégorisation de l’information (Robert, 2005). Pour raisonner, il faut organiser et structurer l’information en catégories, établir des liens entre elles, sélectionner et appliquer des règles logiques nécessaires sur ces informations. La conception de notre modèle du domaine Muse-Expert a fait appel à la mise en œuvre de ces théories. La catégorisation, dans ce cas, réfère à l’organisation de la connaissance, la distinction des règles d’inférences (valides et invalides), la décomposition des informations de chaque problème sur lesquels le système doit raisonner et la représentation des structures/modèles dont ce dernier est doté.

3. Conception participative du module expert

Sur le plan architectural, Muse-Logique est constitué des trois modules classiques d’un système tutoriel intelligent (Nkambou et al., 2010) : un module expert, un module tuteur et un modèle de l’apprenant. L’environnement d’apprentissage donne accès à une banque de problèmes de raisonnement logique générés dans des situations variées. Chaque module offre une interface qui permet sa manipulation individuelle par un utilisateur.

Comme présenté dans la figure 1, le module Muse-Logique Expert met en œuvre aussi bien les habiletés et connaissances en raisonnement logique que les mécanismes de raisonnement connexes (syntaxique et sémantique des règles du système logique donné).

Figure 1 • Composants du module Muse-Logique Expert

En fait, puisque nous prévoyons de couvrir plusieurs systèmes logiques, Muse-logique Expert comporte un contrôleur général dont le but est de sélectionner la logique la plus pertinente dans laquelle la situation (de l'énoncé du problème actuel) s’adapte. Pour ce faire le système s’appuie sur des méta-connaissances pour rechercher des motifs (marqueurs de chaque système logique fournis par les experts) dans la situation qui offre une meilleure prédiction, conduisant à la sélection du système logique approprié. Dans cet article, nous nous concentrons uniquement sur un système logique (la logique classique des propositions).

3.1. Spécification de la mémoire sémantique et procédurale de la logique propositionnelle

La conception participative de chaque composant du module expert a été soigneusement réalisée dans l'équipe. Tout d'abord, nous avons étudié le domaine de la logique propositionnelle ce qui nous a amenés à la spécification complète de tous les concepts qui lui sont liés, puis conduits à une ontologie de domaine que nous avons implémentée comme un modèle OWL. L'ontologie formelle a ensuite été validée lors d’une séance de travail avec les experts logiciens.

L'équipe a ensuite entrepris d’éliciter le processus de déclenchement des connaissances procédurales. Cette démarche a abouti à la spécification de toutes les règles d'inférence logique dans la logique propositionnelle y compris les règles valides et non-valides. Huit règles d'inférence valides ont été spécifiées, deux pour chacun des quatre opérateurs binaires de base de la logique propositionnelle (conjonction, disjonction, implication et incompatibilité). Durant ce processus, les experts logiciens et psychologues du raisonnement ont travaillé ensemble sur la validation empirique de certaines preuves liées à des concepts logiques « mal définis » tels que les constructions d'incompatibilité. L'étude des huit autres règles non-valides spécifiées a conduit à l’élaboration du catalogue des erreurs de raisonnement. Les erreurs de raisonnement ont été divisées en deux catégories : les sophismes (inférences invalides) et les suppressions d'inférences valides.

Les sophismes sont des erreurs de raisonnement logique dans lesquelles le raisonneur ne parvient pas à trouver le bon lien entre les prémisses et la conclusion des règles en cause. Quant aux suppressions d'inférences valides, elles se produisent quand il ou elle ajoute de nouvelles informations dans les prémisses rendant impossible la conclusion.

3.2. Élaboration des méta-structures du raisonnement en logique propositionnelle

L’équipe a examiné en détail l’ancrage sémantique du raisonnement à travers les structures métalogiques comme les treillis de Boole ou encore les groupes de Klein. En fait, le raisonnement logique a été considéré à la fois dans ses composantes syntaxique et sémantique. Quand la logique associe ainsi le syntaxique et le sémantique, la notion de structure devient centrale. Un système logique est fait de structures. Une structure est un ensemble d’objets doté de relations (comme >, = ...) et/ou d’opérations (comme +, x ...). Une structure qui permet de composer de nouveaux objets par des opérations est une structure algébrique, tandis qu’une structure de relations entre des objets est une structure d’ordre. Chaque structure formelle se distingue par ses connecteurs ou ses opérateurs et par les propriétés que possèdent ces relateurs ou opérateurs. La logique classique est régie par des structures logiques telles que l’algèbre de Boole et une structure d’ordre appelée « treillis de Boole ». Les logiques non classiques peuvent être obtenues par des affaiblissements ou des élargissements de l’algèbre de Boole ou du treillis de Boole. Dans cette perspective, l’apprentissage de différents systèmes logiques peut être vu comme étant l’acquisition de différentes structures algébriques pour catégoriser le monde et de différentes structures d’ordres pour établir des hypothèses de dépendance causale entre ces catégories. Nous traitons alors les stratégies de type 1 causant les erreurs logiques comme des simplifications des structures à l’œuvre dans les raisonnements. D’un point de vue métacognitif, nous utilisons ces métastructures pour illustrer le raisonnement erroné, interprété comme un mauvais parcours de celles-ci ou comme un écrasement de structure (groupe de Klein) (Robert et Brisson, 2016).

3.3. Des situations de raisonnement multiples

Le raisonnement logique n’est pas un processus absolu dans le sens que le même type de raisonnement peut être difficile à appliquer d’une classe de situations à une autre. Être compétent dans l’usage du modus ponendo ponens (MPP) dans une situation donnée (par exemple en situation descriptive causale avec peu de possibilités) n’implique pas qu’on le sera dans une autre (par exemple en situation descriptive causale avec beaucoup d’alternatives). Cette thèse est soutenue par une étude menée par les membres de l’équipe Muse-Logique dans laquelle certains sophismes étaient attribuables à la difficulté de trouver des contre-exemples dans un raisonnement mettant en œuvre l’affirmation du conséquent (Brisson et al., 2014), (Markovits, 2014). Nous avons examiné, avec les experts logiciens et les psychologues du raisonnement membres de l’équipe, différentes familles de situation pouvant engendrer une variation du niveau de difficulté d’un type de raisonnement. Nous avons ainsi établi six familles de situations descriptives (tableau 1).

Tableau 1 • Familles de situations de raisonnement (classes de problèmes)

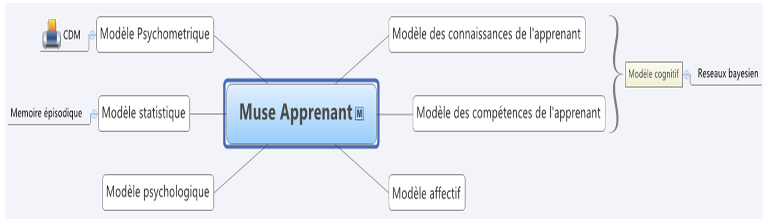
La catégorisation fournit non seulement une base permettant de classer les compétences en raisonnement, mais permet aussi d’organiser les activités d’apprentissage du raisonnement. Le raisonnement normatif a été exclu parce que les expérimentations du raisonnement sur du contenu normatif ont montré une excellente performance tant des adultes que des enfants (Cloutier, 2016), (Girotto et al., 1989). Une explication de cet effet de contenu est que la cognition humaine comporte un module spécialisé pour raisonner sur les normes sociales (Girotto et al., 1989).

La catégorisation nous a permis d’établir une mémoire procédurale de la logique des propositions comportant 96 éléments de connaissances, soit 48 éléments de connaissances valides et 48 non valides. Par ailleurs cette contextualisation aide à classifier les exercices à soumettre à l’apprenant et définit un cadre précis pour l’évaluation des compétences de l’apprenant. Par exemple, la catégorie « Descriptive causale et concrète avec peu d’alternatives » (DCCFA) comporte des exercices avec un contenu familier, facile à comprendre, et dont l’antécédent présente très peu d’alternatives. Par exemple, pour l’antécédent « si un chien a des puces, alors il se gratte constamment », il pourrait y avoir deux alternatives : « avoir la peau sèche » ou « une maladie de la peau ». Par contre, dans la catégorie « Causale avec beaucoup d’alternatives », en plus d’un contenu familier, facile à comprendre, il y a beaucoup d’alternatives causales. Par exemple, l’antécédent de « Si on lance une pierre dans la fenêtre, alors la fenêtre se brisera » a un grand nombre d’alternatives : « lancer une chaise dans la fenêtre », « lancer une brique dans la fenêtre », « collision avec une voiture », « tempête tropicale », « frapper la fenêtre avec un bâton », « se projeter dans la fenêtre », etc.

Dans Muse-Logique, les exercices sont présentés sous forme de syllogisme et offrent des choix de réponse. Par exemple :

- Règle : Si je lance une pierre dans la fenêtre, alors la fenêtre brisera.

- Information : La fenêtre est brisée.

- Que peut-on conclure ?

• On a lancé une pierre dans la fenêtre.

• On n’a pas lancé une pierre dans la fenêtre.

• On ne peut conclure.

4. Le modèle de l’apprenant

Le modèle de l’apprenant dans Muse-Logique comporte plusieurs dimensions (figure 2). La mémoire épisodique garde la trace des exercices effectués par l’apprenant ainsi que tous les éléments de performance reliés. Le modèle cognitif est principalement un modèle bayésien dont les nœuds sont les 96 unités de connaissances liées au raisonnement. C’est de l’approche de construction du modèle cognitif dont nous parlerons dans la suite de cet article. 

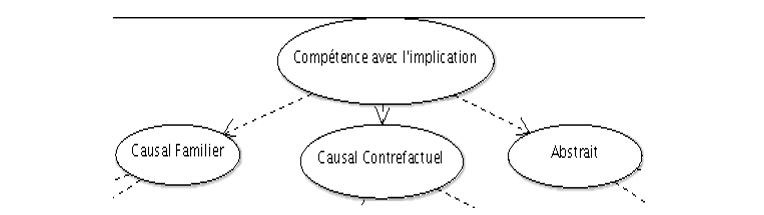
Figure 2. • Composants du modèle de l’apprenant dans Muse-Logique

Lorsqu’un réseau bayésien (RB) est utilisé pour la modélisation d’un apprenant, des nœuds observables représentent un ensemble d’items et des nœuds cachés (ou latents) représentent une compétence du domaine d’apprentissage. Les liens entre les nœuds représentent la dépendance bayésienne entre la réussite d’un item et une compétence du domaine, entre deux compétences ou entre deux items. Le modèle de l’apprenant généré par cette structure contient donc deux parties : le modèle de la compétence et le modèle de la performance (Almond et al., 2007). Ce formalisme est tout à fait adéquat pour représenter les compétences pertinentes au raisonnement déductif ainsi que les performances aux différents items. Pour le modèle de l’apprenant de Muse-Logique, nous avons donc construit la structure d’un RB en tant qu’outil d’évaluation automatique du raisonnement conditionnel. Les probabilités a priori ainsi que les relations d’influence entre les différentes unités de connaissance ont été initialement établies par les experts. Certains nœuds sont directement connectés aux exercices de raisonnement (items). Certains nœuds du réseau sont bien entendu liés aux inférences invalides (sophismes ou suppressions d’inférence). On entretient ainsi et de manière automatique le modèle de l’apprenant sur chaque unité de connaissances (valide ou erronée). Les statistiques sur la performance sont calculées à partir des données stockées dans la mémoire épisodique.

4.1. Un réseau bayésien initial à validation experte

La structure à validation experte que nous avons construite et l’identification des compétences visées pour une maîtrise complète du raisonnement conditionnel sont basées sur les effets du contenu dans le raisonnement, sur l’approche développementale de Markovits (Markovits, 2014), ainsi que sur l’approche formelle de Robert et Brisson (Robert et Brisson, 2016). Les compétences visées sont l’inhibition des conditions contraignantes, la génération des antécédents alternatifs ainsi que la bonne gestion mentale des trois situations pertinentes pour l’implication (i.e. les trois rangées vraies du connecteur). Ces trois compétences de base sont déclinées dans trois situations différentes, soit le raisonnement avec du contenu familier, contrefactuel ou abstrait. Les nœuds au bas de la structure représentent les types d’items qui seront sélectionnés par le système, soit les quatre formes logiques du raisonnement conditionnel.

Nous exposons ci-dessous les différentes portions de la structure du RB pour le raisonnement conditionnel. La figure 3 montre le haut de la structure. Le premier nœud représente la compétence globale. La structure montre des liens de dépendance entre ce dernier et les trois nœuds qui lui succèdent.

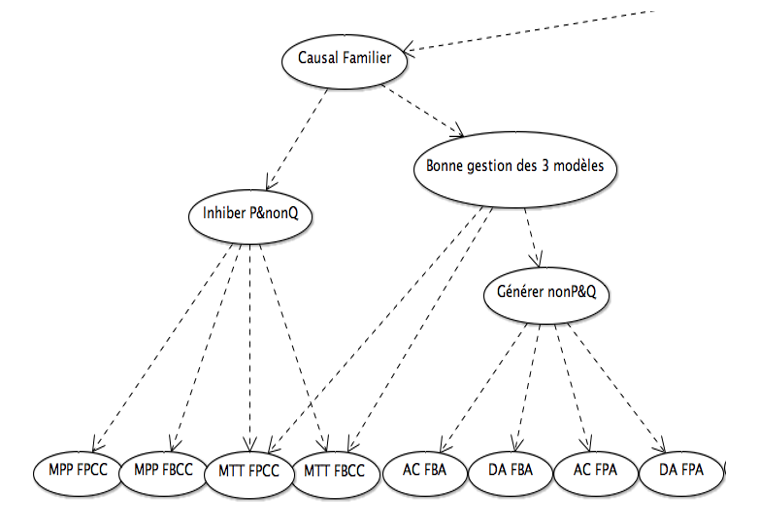
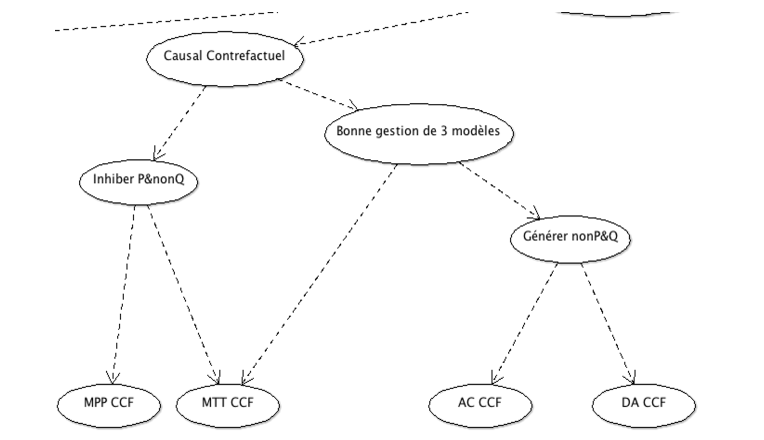
Figure 3 • Tête du RB pour le raisonnement conditionnel

En le lisant de gauche à droite, la première branche du RB expose les compétences pertinentes pour le raisonnement conditionnel avec du contenu de plus en plus difficile. Le premier nœud enfant du nœud racine « Compétence avec l’implication » est donc « Causal Familier », suivi de « Causal contrefactuel » et de « Abstrait ».

La figure 4 expose les compétences pertinentes pour le raisonnement conditionnel avec du contenu familier.

Figure 4 • Portion du RB pour le raisonnement conditionnel familier

Dans cette structure, le nœud « Inhiber P&nonQ » représente la capacité d’inhiber les conditions contraignantes de la prémisse conditionnelle, nécessaire pour reconnaître la certitude des inférences valides MPP et MTT. Les nœuds enfants de ce dernier sont donc les nœuds qui représentent le MPP avec peu (MPP FPCC) et beaucoup (MPP FBCC) de conditions contraignantes ainsi que le MTT avec peu (MTT FBCC) et beaucoup (MTT FPCC) de conditions contraignantes.

De plus, le nœud « Bonne gestion des 3 modèles » représente une compétence pertinente aux raisonnements MTT, AC et DA. Cette compétence consiste à garder en mémoire de travail les trois modèles pertinents à une prémisse conditionnelle ou, autrement dit, les trois rangées vraies du connecteur d’implication. Le MPP, de par sa simplicité et de par le fait qu’il peut être réussi même avec une compréhension simplifiée de l’implication, n’est pas un bon indicateur de cette compétence avancée. Nous avons donc déterminé qu’une capacité à répondre correctement aux trois inférences plus complexes (MTT, AC et DA) était le meilleur indicateur de cette compétence.

Le nœud « Générer nonP&Q » représente la capacité de générer les antécédents alternatifs qui serviront de contre-exemples aux conclusions invitées des inférences AC et DA. On retrouve donc parmi ses nœuds enfants ceux qui représentent la compétence avec le AC et le DA avec beaucoup (AC FBA et DA FBA respectivement) et peu (AC FPA et DA FBA respectivement) d’antécédents alternatifs. Le tableau 2 résume la signification de chacun de ces nœuds et donne un exemple pour chacun d’eux.

Tableau 2 • Légende pour les nœuds items familiers

Finalement, les relations de dépendance entre les nœuds de compétences exposés permettront au système de déterminer les probabilités de maîtrise des compétences à partir du patron de réponses de l’apprenant. Plus précisément, un ensemble de bonnes réponses aux items MPP et MTT augmentera la probabilité de maîtriser l’inhibition des conditions contraignantes. Des bonnes réponses aux items AC et DA augmenteront la probabilité de maîtriser la génération des antécédents alternatifs. De plus, un ensemble de bonnes réponses aux MTT, AC et DA augmentera la probabilité d’une bonne gestion des trois modèles pertinents à l’implication. L’évaluation de toutes ces compétences aura un impact sur la probabilité de maîtrise du raisonnement conditionnel avec du contenu familier, ce qui, finalement, aura un impact sur la probabilité de maîtriser le raisonnement conditionnel dans son ensemble.

La figure 5 expose la portion du RB relative au raisonnement avec du contenu contrefactuel. Les nœuds ainsi que les relations de dépendance entre eux sont les mêmes que dans la structure relative au raisonnement avec du contenu familier : la structure réfère aux mêmes processus de raisonnement et aux mêmes compétences visées. La différence est au niveau des nœuds qui représentent les formes logiques. Notons que la distinction entre peu et beaucoup d’alternatives ou de conditions contraignantes n’est plus présente dans cette structure. En effet, la quantité d’antécédents alternatifs et de conditions contraignantes avec des prémisses contrefactuelles est difficilement mesurable et aucune étude n’investigue cette dimension dans la littérature actuelle. Nous nous sommes donc restreints à des nœuds qui représentent la compétence au raisonnement avec les quatre formes logiques avec du contenu contrefactuel, sans distinction supplémentaire.

Figure 5 • Portion du RB pour le raisonnement causal contrefactuel

Le tableau 3 résume la signification de chacun de ces nœuds avec un exemple pour chacun.

Tableau 3 • Légende pour les nœuds items causaux contrefactuels

La figure 6 expose la dernière portion du RB, soit le raisonnement avec du contenu abstrait. Les nœuds « Inhiber P&nonQ », « Bonne gestion des 3 modèles » et « Générer nonP&Q » sont présents, entretiennent les mêmes relations de dépendance et réfèrent à des processus de raisonnement semblables à ceux des structures précédentes. Les nœuds « MPP A », « MTT A », « AC A » et « DA A » réfèrent aux quatre formes logiques avec du contenu abstrait.

Figure 6 • Portion du RB pour le raisonnement causal abstrait

Notons que, comme dans le cas du raisonnement contrefactuel, la distinction quant au nombre d’antécédents alternatifs et de conditions contraignantes n’est pas présente. La raison est toutefois différente. À ce niveau de difficulté du raisonnement conditionnel, le raisonneur doit comprendre que, pour toute prémisse conditionnelle, un antécédent alternatif peut être généré, et ce, indépendamment de son bagage de connaissances. La génération des alternatives, l’inhibition des conditions contraignantes et la gestion des trois modèles demandent donc, à ce niveau, une compréhension plus abstraite que dans les situations précédentes.

Le tableau 4 fournit des exemples pour des nœuds qui représentent les quatre formes logiques avec du contenu abstrait (abrégé A).

Tableau 4 • Légende pour les nœuds items causaux abstraits

Finalement, la structure globale du RB rend compte de la hiérarchie entre les compétences appartenant aux trois niveaux de contenu. Ainsi, les compétences relatives au raisonnement abstrait demandent une certaine maîtrise des compétences relatives au raisonnement contrefactuel, qui elles-mêmes demandent une certaine maîtrise des compétences relatives au raisonnement familier.

4.2. Amélioration de la structure et du processus d’initialisation du réseau bayésien par le CDM

Allié au réseau bayésien construit avec les experts, un modèle de diagnostic cognitif de type Cognitive Diagnosis Model (CDM) (Rupp et al., 2007) a été entrainé à partir des données collectées lors d’une expérimentation avec 294 participants sur une banque de 48 exercices. Pour ce faire, une Q-Matrice (dont une portion est présentée dans le tableau 5) mettant en évidence le croisement entre les items (48 items regroupés en 16 classes) et les unités de connaissances ou habiletés cognitives (9 classes) a été soigneusement élaborée avec l’aide des experts logiciens.

Tableau 5 • Q-Matrice dans MUSE-Logique

Nous avons ensuite entraîné un modèle DINA (plus précisément G-DINA) (de la Torre, 2009), (de la Torre, 2011) sur les 294 patrons de réponses, ce qui a permis d’estimer des paramètres utiles comme guess, la probabilité qu’un apprenant puisse répondre correctement à un exercice sans avoir les habiletés nécessaires, et slip, pour la probabilité d’une mauvaise solution alors qu’on disposait des habiletés nécessaires, ou encore l’indice de discrimination associé à chaque item de la Q-Matrice qui permet de déterminer leur pertinence dans la mesure de la compétence ciblée. Les sous-sections suivantes présentent quelques aperçus de l’analyse des résultats.

4.2.1. Qualité de l’ajustement du modèle

Bien que l’évaluation de l’ajustement de modèle se fasse généralement via le critère d'information Akaike (AIC) et le critère d'information bayésien (BIC), un indicateur absolu de la qualité de l'ajustement pour le modèle CDM est la mesure χ2, test du « khi-deux » par paire d'items (Chen et al., 2013), (Chen et al., 2018). Cette mesure indiquera que le modèle est inadéquat si la valeur-p de la mesure χ2 maximale est supérieure à 0,01, le seuil de signification asymptomatique fixée selon la littérature (Groß et al., 2016). Dans notre cas, le χ2 maximal = 33,95 avec p = 6,793316×10⁻⁷ (largement < 0,01), confirmant ainsi que le modèle obtenu est adéquat.

4.2.2. Probabilités marginales des compétences

Le tableau 6 ci-dessous montre la probabilité moyenne de maîtrise pour chaque compétence.

Tableau 6 • Distribution des compétences

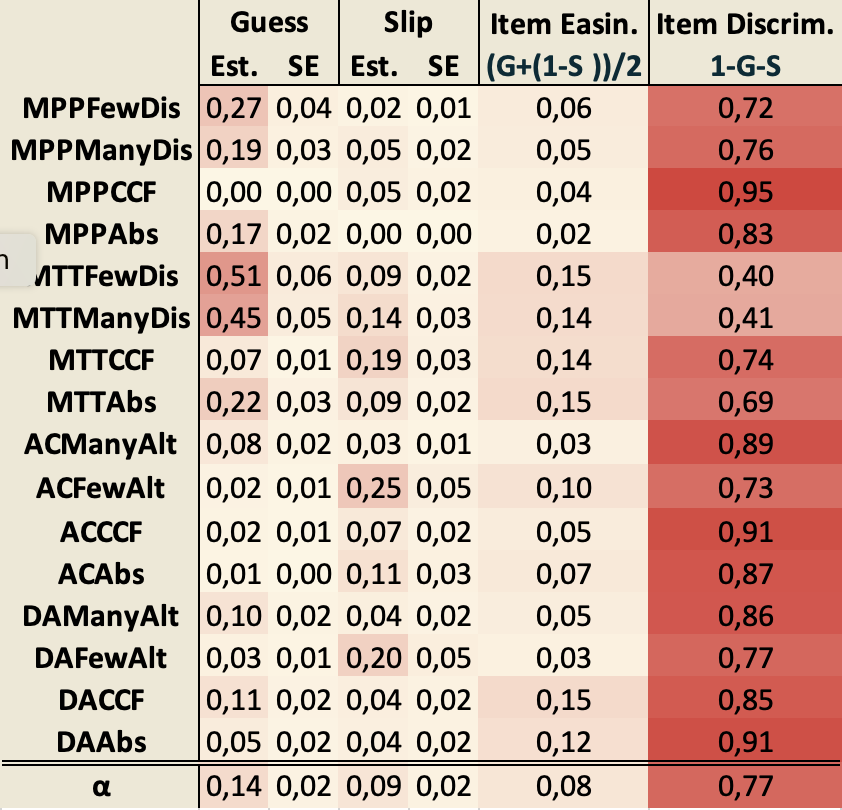
La compétence la plus difficile semble être « Inhibit counterfactual », avec une probabilité moyenne de 44,3 % de maîtrise. En effet, cette compétence exige d'inhiber les conditions invalidantes aux énoncés conditionnels contrefactuels, ce qui n’est pas facile.

Cette observation corrobore le fait que l’indice de discrimination d’un item (IDI) le plus élevé est celui du MPP contrefactuel comme on peut le voir dans le tableau 7. Rappelons que l’IDI mesure la capacité d'un item à faire la distinction entre les répondants compétents et ceux qui ne le sont pas (selon la compétence sous-jacente). Plus cet indice est faible, plus l'item est pertinent pour la mesure de cette compétence.

Par ailleurs, la probabilité beaucoup plus élevée pour les compétences avec le niveau familier suggère une séparation avec les deux autres niveaux, avec une différence entre le niveau contrefactuel et le niveau abstrait.

4.2.3. L’estimation des paramètres guess, slip & IDI

Tout d'abord, comme on peut le voir dans le tableau 7, nous avons noté une estimation élevée du guess et une faible IDI pour les deux MTT avec un contenu familier. Cela pourrait s'expliquer par le fait qu'une interprétation biconditionnelle de la prémisse majeure conduit à la bonne réponse au MTT alors même que la compétence avec le conditionnel n'est pas acquise. Cependant, dans l'ensemble, tous les autres éléments ont une bonne IDI. Il convient également de noter que l'IDI du MPP contrefactuel est la plus élevée.

Le succès à cet item semble donc le meilleur moyen de montrer que le raisonnement conditionnel est maîtrisé. Cela va dans le sens des observations tirées des probabilités marginales des compétences discutées plus haut

Tableau 7 • Probabilités Guess, Slip et IDI

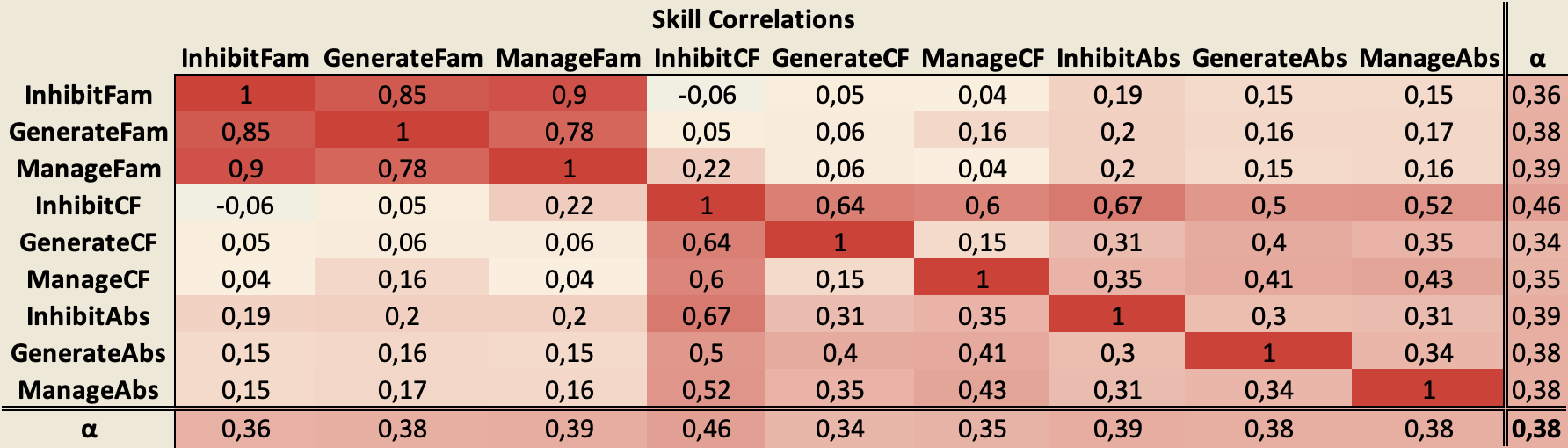
4.2.4. Corrélations tétrachoriques

Un des résultats de l’approche CDM est l’estimation des corrélations entre les habiletés. Le tableau 8 illustre les corrélations établies par notre modèle.

Tableau 8 • Corrélations entre compétences

Selon la taille de notre échantillon, les corrélations supérieures à 0,33 sont considérées comme significatives pour un seuil de coefficient de corrélation α = 0,05 (Guilford et Lyons, 1942). Nous avons donc appliqué ce critère dans notre analyse subséquente en illustrant aussi le coefficient de corrélation moyen (α) de chaque compétence.

Une observation que l'on peut tirer de ces corrélations tétrachoriques est que les compétences ayant un contenu familier sont fortement corrélées à d'autres compétences du même niveau de contenu, alors que les corrélations avec les niveaux contrefactuels et abstraits ne sont pas significatives. Cependant, les compétences au niveau contrefactuel sont corrélées entre elles et avec les compétences au niveau abstrait, et vice-versa. Dans l'ensemble, cela semble indiquer une fois de plus une séparation entre le niveau familier du contenu et les deux autres niveaux.

4.2.5. Autres résultats et impacts sur le réseau bayésien initial

Plusieurs autres résultats importants du modèle ne sont pas rapportés dans cet article. C’est par exemple le cas de la matrice posterior qui associe les patrons de réponses aux profils de compétence des apprenants, offrant ainsi la possibilité d’estimer le vecteur de compétence initial d’un nouvel apprenant, utilisé pour l’initialisation du réseau bayésien représentant son modèle cognitif. Ainsi, les probabilités a priori du réseau bayésien initial sont estimées de cette manière plutôt que de considérer la chance. Par ailleurs, le modèle CDM que nous avons construit pour MUSE-Logique a permis de valider et d’ajuster la structure du réseau initialement construit avec les experts, aboutissant ainsi à une structure plus efficace informée à la fois par les données (bottom-up) et les experts (top-down).

4.3. Évaluation et prédiction des performances par le BKT et le DKT

La modélisation de l’apprenant dans un système visant l’apprentissage passe avant tout par la modélisation de sa connaissance, puisque c’est cette dernière que le système vise à améliorer. L’approche la plus populaire pour modéliser la connaissance de l’usager est le Knowledge Tracing (KT) (pour traçage des connaissances). Le KT vise à modéliser la façon dont les connaissances des apprenants évoluent pendant l’apprentissage. La connaissance est modélisée sous forme d’une variable latente et est mise à jour en fonction des performances de l’usager-apprenant au fur et à mesure qu’il effectue les tâches. Cette approche est formalisée comme suit :

Sachant les interactions d’un apprenant jusqu’au temps t (x₁ ... x_t) sur une tâche d’apprentissage particulière, quelle performance va-t-il accomplir au temps t + 1, l’objectif étant d’estimer la probabilité p (x_t+1|x₁..., x_t) ? Il existe plusieurs solutions pour estimer cette probabilité entre autres le Bayesian Knowledge Tracing (BKT) et le Deep Knowledge Tracing (DKT).

4.3.1. Pallier les limites du BKT et du DKT classiques par une approche hybride

Nous avons montré dans les sections précédentes comment le réseau bayésien de Muse-Logique a été construit et validé. Nous expliquons dans cette section comment le BKT y est appliqué. Rappelons que le BKT (Corbett et Anderson, 1994) est une approche de modélisation latente de l’apprenant par un réseau bayésien qui peut être soit appris à partir des données soit défini par les experts. Le BKT est un cas particulier des chaînes de Markov cachées où les connaissances de l’usager sont représentées par un ensemble de variables binaires (la connaissance est maîtrisée ou non). Les observations sont aussi binaires : un usager peut soit réussir soit échouer à résoudre un problème (Yudelson et al., 2013). Il ne peut pas réussir à 30 % ou à 70 % par exemple. Cependant, il existe une certaine probabilité (G, paramètre guess) que l’usager donne une réponse correcte à un exercice X sachant qu’il ne maîtrise pas la connaissance liée à cet exercice. Pareillement, un usager qui maîtrise une connaissance donnera généralement une réponse correcte sur les exercices liés à cette connaissance, mais il existe une certaine probabilité (S, le paramètre slip) que l’usager n’y réponde pas correctement. Le modèle standard de BKT est donc défini par quatre paramètres : l’état de connaissance initiale, la vitesse d’apprentissage (learning parameters), les probabilités de slip et de guess (mediating parameters). En règle générale, le BKT utilise les informations a priori sur les connaissances, telles que les probabilités conditionnelles et les probabilités de maîtrise des connaissances, pour mesurer les progrès de l’apprentissage des usagers. Dans un tel contexte, la performance (échec ou réussite) est la variable observée et les connaissances sont les variables latentes. L’inférence bayésienne est utilisée pour déterminer les probabilités recherchées. Le BKT est classique et, au-delà de Muse-Logique, a été utilisé avec succès dans plusieurs domaines d’apprentissage, entre autres la programmation informatique (Kasurinen et Nikula, 2009) et la lecture (Beck et Chang, 2007).

Toutefois, l’utilisation d’un réseau bayésien implique parfois de définir manuellement les probabilités a priori et d’étiqueter manuellement les interactions avec des concepts appropriés. De plus, les données de réponses binaires utilisées pour modéliser les connaissances, les observations et les transitions imposent une limite aux types d’exercices pouvant être modélisés. Le DKT a donc été proposé afin de résoudre les problèmes du BKT. Sans nécessairement entrer dans une description détaillée du DKT original (Piech et al., 2015), notons que deux limites lui sont facilement reconnues, notamment :

- sa faible capacité à bien généraliser sur les connaissances plancher/plafond (c’est-à-dire celles avec peu de données d’entraînement, par exemple un faible taux d’échec ou un taux élevé de succès) ;

- la non intégration des connaissances expertes, une source importante déjà éprouvée dans le cadre des BKT à validation experte.

Ces deux limites nous ont poussés à développer un DKT amélioré dit hybride (Tato et Nkambou, 2019) qui a été utilisé dans le cadre de cette étude. Une des améliorations a porté sur l’injection des connaissances expertes à travers un mécanisme attentionnel tel qu’illustré dans la figure 7.

En d’autres termes, le réseau de neurones « consultera » ou « portera attention sur » les connaissances expertes avant de prendre la décision finale (émettre la prédiction finale (y’_t)). Les « connaissances » peuvent être représentées sous plusieurs formes. Dans le cas de MUSE-Logique (cf. section 4.3.2), elles sont incarnées par le réseau bayésien conçu intégralement par les experts. L’importance que le modèle neuronal accordera à ce que ces connaissances prédisent comme sortie est calculée au moyen de pondération de l’attention (W_a et W_c).

Au fur et à mesure de l’apprentissage, le réseau saura quelle importance il accordera à chacune des prédictions provenant de la branche des connaissances, en fonction des essais/erreurs qu’il aura commis. Les poids Ⱳ_a représentent l’importance de chaque caractéristique apprise par l’architecture neuronale (y_t) par rapport à chaque caractéristique extraite à partir des connaissances. Les poids Ⱳ_c représentent l’importance des prédictions faites à partir des connaissances (via le vecteur de contexte) et des caractéristiques apprises (y_t) pour l’estimation du vecteur de prédiction finale. Ainsi, le modèle se concentrera sur ce que dit l’expertise dont les connaissances a priori et a posteriori (intégrées dans le réseau bayésien qui modélise l’apprenant), avant de prendre une décision. En fusionnant ainsi les connaissances des experts avec l’architecture neuronale à l’aide du mécanisme d’attention, le modèle traite de façon itérative les connaissances en sélectionnant le contenu pertinent à chaque étape.

Figure 7 • Modèle DKT hybride

À chaque instant t, le modèle déduit, par une couche de concaténation, l’état caché attentionnel (le vecteur α_t). Cette couche combine la prédiction actuelle du système neuronal (y_t) et le vecteur de contexte côté expert (C^e_t) pour déduire le vecteur attentionnel α_t comme suit :

α_t = tan(Ⱳ_c[C^e_t ; y_t])

Le vecteur de contexte C^e_t est calculé comme étant la moyenne pondérée, selon a_tsur chaque entrée du vecteur de connaissances expert (e)¹ comme suit :

avec

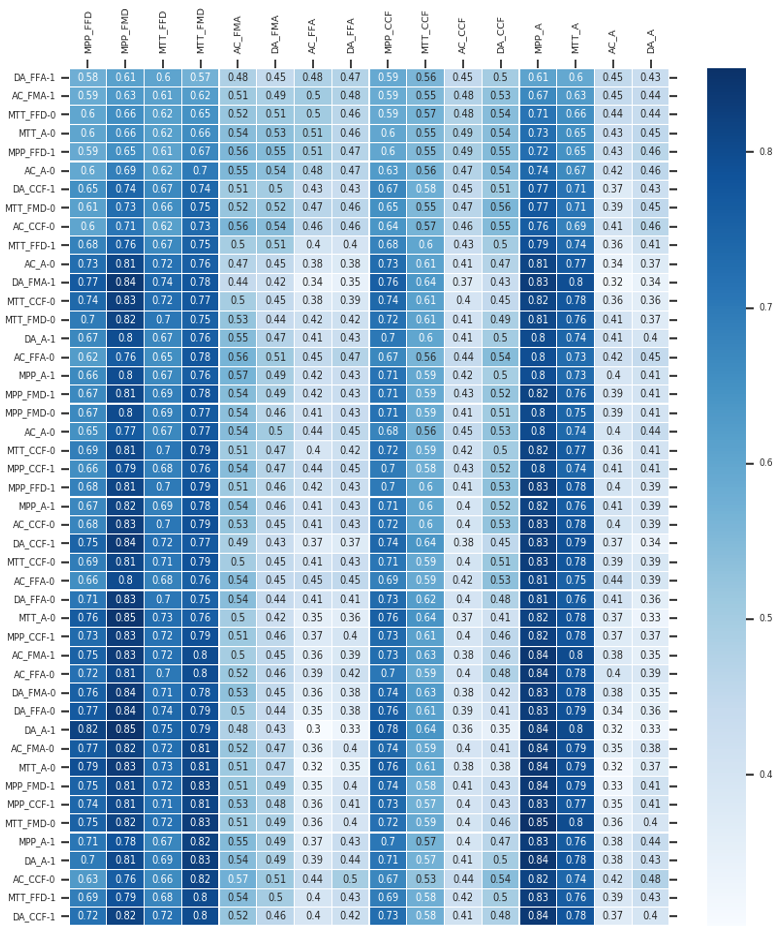
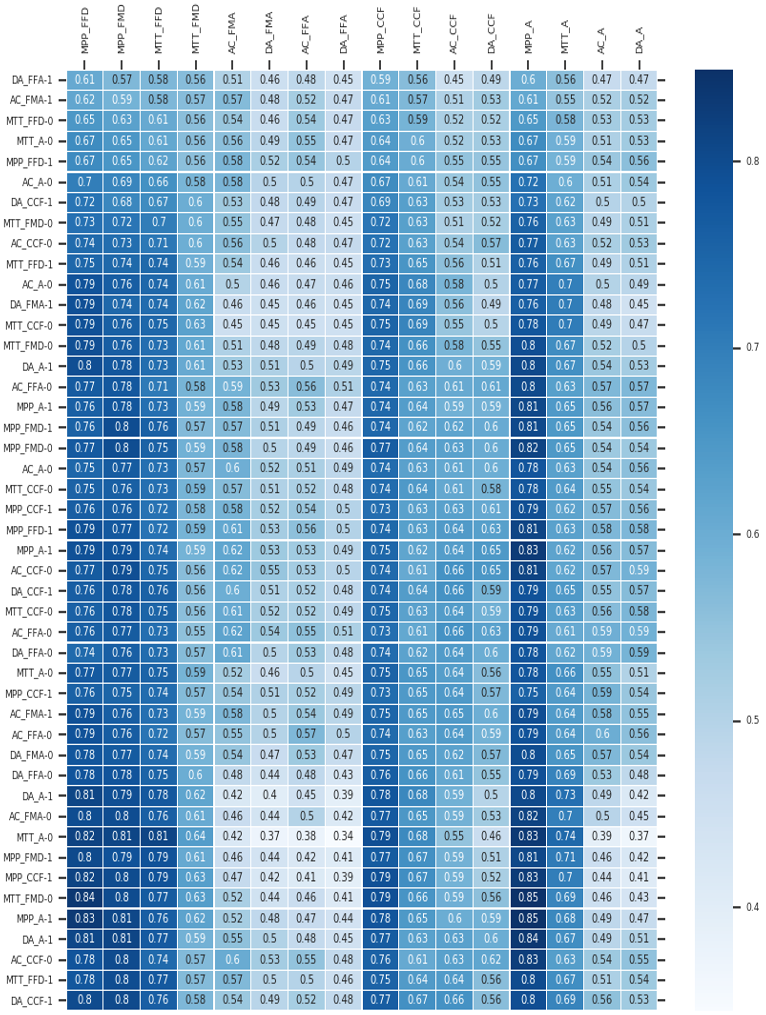
et

score(e_k, y_t) = e_k y_t  Ⱳ_a + b

Dans ces formules, la variable e représente un vecteur de longueur égale à la taille du vecteur à prédire. Chaque élément e_k du vecteur e représente la probabilité de maîtrise de la k-ième connaissance selon les prédictions de l’expert (c’est à dire du réseau bayésien).

1 ≤ k ≤ s, e est la prédiction faite à partir des connaissances a priori et a posteriori, y_t est la prédiction actuelle faite par l’architecture neuronale et s est la taille du vecteur prédit (le nombre de classes à prédire).

Le score est un vecteur basé sur le contenu qui calcule la corrélation (score d’alignement) entre les connaissances expertes et les caractéristiques latentes apprises par l’architecture neuronale, tout en considérant le biais (b).

Ainsi, le score définit comment les connaissances expertes et les caractéristiques apprises à partir des données sont alignées. Le modèle attribue un score α_t,k à la paire d’entités à la position t et aux connaissances expertes (e_k,_,y_t), en fonction de leur correspondance. L’ensemble des α_t,k sont des pondérations définissant à quel point chaque caractéristique de la donnée provenant de l’expert doit être prise en compte pour chaque sortie (prédiction finale).

Le système (architecture) neuronal est un DKTm, une version du DKT original dans laquelle nous utilisons un masque pour obliger une attention particulière de l’apprentissage du réseau sur les connaissances plancher/plafond (pour une meilleure généralisation sur ces connaissances). Ce principe est détaillé dans (Tato et Nkambou, 2019). En bref, l’injection de la connaissance experte dans le réseau de neurones se fait par un mécanisme attentionnel induit par le vecteur α_t résultant d’une combinaison des vecteurs de sortie des sous-systèmes neuronal et bayésien (y_t et C^e_t), tel qu’illustré dans la figure 7.

4.3.2. Prédiction des performances par le DKT dans MUSE-Logique

Le traçage des connaissances dans MUSE-Logique par le BKT appliqué sur la version du réseau bayésien à validation experte uniquement (sans aucune amélioration par le CDM ou toute autre approche utilisant les données) produit des déductions avec une précision relative intéressante (Accuracy de 65 %). Notre hypothèse est qu’en utilisant ce réseau bayésien comme connaissance experte (a priori) nous pouvons mettre en place un nouveau modèle de traçage de connaissances hybride plus performant, qui le fusionne avec le DKT. Pour ce faire, nous avons conduit des tests qui visent à évaluer la capacité de traçage de connaissance du DKT hybride versus le réseau bayésien seulement.

Nous avons utilisé les mêmes données collectées dans le cadre de notre étude sur l’amélioration du réseau bayésien par le CDM (section 4.2). Dans notre ensemble de données, chaque ligne de données représente un participant (un total de 294 données et une longueur de séquence de 48). Cette quantité de données est trop limitée pour entraîner un modèle d’apprentissage profond. Cependant, en les combinant aux connaissances des experts, nous voyons une différence substantielle dans les résultats. Les exercices ont été encodés en utilisant les 16 connaissances (compétences) de base identifiées, ce qui signifie que les questions relatives à la même connaissance sont encodées avec le même Id (1∼16). Les connaissances avec peu de données d’entraînement (connaissances planchers/plafonds) sont déterminées par une comparaison de la moyenne des bonnes réponses obtenues pour chaque connaissance. Dans le tableau 9, nous avons fait la moyenne de toutes les réponses pour chaque connaissance. Les connaissances planchers sont celles dont les valeurs moyennes sont les plus basses et les connaissances plafonds sont celles dont les moyennes sont les plus élevées.

La deuxième et la dernière partie de notre nouvelle fonction de perte portent donc sur ces connaissances. Puisque le RNN n’accepte qu’une longueur fixe de vecteurs en entrée, nous avons utilisé un codage one-hot pour convertir la performance des apprenants en des vecteurs de longueur fixe dont tous les éléments sont à 0 sauf un seul qui est à 1. Le 1 dans ce vecteur indique deux choses : quelle connaissance a été évaluée et si la réponse à la question portant sur cette connaissance est correcte.

Tableau 9 • Distribution des réponses par rapport aux connaissances difficiles à maîtriser (moyenne<0.4) et connaissances faciles à maîtriser (moyenne>0.9)

Nous avons utilisé 3 modèles : le DKT, le DKT où nous avons appliqué un masque à la fonction de perte (DKTm) (Tato et Nkambou, 2019), et le DKTm hybride avec connaissances a priori (DKTm+BN) décrit à la figure 7. Nous avons utilisé AAdam, une version accélérée de Adam (Tato et Nkambou, 2020), comme algorithme d’optimisation de l’apprentissage. Nous avons utilisé 20 % des données pour les tests et 15 % pour la validation.

Comme mentionné ci-dessus, le BN à lui seul a une performance de 65 % de précision globale sur ces données. Le résultat est évalué à l’aide de la métrique F1score sur chaque connaissance (traitée comme 2 classes : réponses correctes et incorrectes) en jeu et sur la précision globale du modèle. Les modèles ont été évalués sur 20 expériences différentes et la moyenne des résultats finaux a été calculée. Le paramètre de régularisation a été fixé à 0.10 dans toutes ces expériences. Notre implémentation du modèle DKT avec Keras a été inspirée de l’implémentation faite par Khajah, Lindsey et Mozer (Khajah et al., 2016).

4.3.3. Analyse des résultats du DKT dans MUSE-Logique

Nous avons tout d’abord observé les résultats en suivant les interactions pour 1 apprenant. Ensuite, nous avons étudié les interactions avec l’ensemble des étudiants et avons itéré 20 fois afin de considérer la moyenne des prédictions des différents modèles. L’analyse des performances de la prédiction pour 1 étudiant est présentée à la section 4.3.3.1 alors que l’analyse des performances prédictives moyennes des modèles pour l’ensemble des apprenants est présentée à la section 4.3.3.2.

4.3.3.1. Prédiction pour un seul apprenant

Les figures A1, A2 et A3 en annexe illustrent une visualisation du traçage en temps réel des connaissances en raisonnement logique d’un apprenant. Dans la visualisation, nous ne montrons que les prédictions dans le temps pour les 48 exercices. Les colonnes représentent la compétence mise en jeu dans la question posée à l’instant t, suivie de la réponse réelle de l’apprenant (il y a 48 lignes représentant les 48 questions et 16 colonnes pour les 16 compétences de base en jeu). Les couleurs et les probabilités à l’intérieur de chaque case indiquent la probabilité prédite par les modèles que l’apprenant répondra correctement à une question liée à une compétence (en ligne) à l’instant suivant. Plus la couleur est foncée, plus la probabilité est élevée.

L’apprenant répond d’abord correctement à une question relative à la connaissance DA_FFA (DA_FFA - 1) et à une question relative à la compétence AC_FMA (AC_FMA - 1) et ensuite échoue à la question portant sur la connaissance MTT_FDD (MTT_FDD - 0). Dans les 45 questions suivantes, l’apprenant résout une série de problèmes liés aux 16 connaissances impliquées.

Dans la figure A1, on constate facilement que le DKT est incapable de faire des prédictions précises sur les compétences avec peu de données, surtout celles qui sont difficiles à maîtriser.

Les figures A2 et A3 illustrent la prédiction des performances du même apprenant avec les 2 variantes de DKT que nous avons proposées. Dans ce scénario, l’apprenant a donné 2 bonnes réponses sur 3 sur la compétence AC_FMA (5^ème colonne) et nous voyons que le DKTm et le DKTm+BN sont capables de mieux prédire cette information, comparativement au DKT.

Notre première version du DKT (DKTm, figure A2) surpasse le DKT initial (figure A1) pour le traçage de toutes les connaissances en jeu. De plus, le DKTm amélioré avec la connaissance experte (le réseau bayésien) en utilisant notre solution hybride (DKTm+BN, figure A3) surpasse tous les autres modèles par sa capacité de prédiction avec peu de données.

4.3.3.2. Analyse du pouvoir prédictif des modèles pour l’ensemble des apprenants

Chaque fois qu’un apprenant répond à un exercice, les modèles mettent à jour ses connaissances de façon à pouvoir prédire s’il répondra correctement ou non à un exercice portant sur chaque connaissance lors de sa prochaine interaction. Les résultats de la performance des trois variantes de DKT après 20 itérations, sont présentés dans les tableaux 10 et 11

Tableau 10 • Le DKT, le DKTm et le DKKm+BN sur les connaissances difficiles

Dans le tableau 10, la dernière colonne est la précision globale du modèle. Pour chaque connaissance, la première colonne correspond à la valeur du f1score pour la prédiction des réponses incorrectes et la deuxième colonne pour la prédiction des réponses correctes. La meilleure valeur pour chaque connaissance est en gras.

Tableau 11 • Le DKT, le DKTm et le DKKm+BN sur les éléments de connaissances faciles

Pour les connaissances faciles à maîtriser (par exemple le MPP), tous les modèles prédisent toujours que les apprenants donneront des réponses correctes (le score F1 des réponses incorrectes est 0 pour le DKT et presque 0 pour les deux autres modèles) même après l’application du masque sur la fonction de perte. Ceci est dû principalement au fait que l’ensemble des données comporte très peu de réponses incorrectes (6 au total) pour cet élément de connaissance.

Nous avons testé les modèles avec des valeurs élevées du paramètre de régularisation λ (initialement fixé à 0.10) et nous avons obtenu des valeurs de f1score égales à environ 0.6 pour les bonnes réponses et à environ 0.7 pour les mauvaises réponses. Ce résultat peut être satisfaisant dans d’autres contextes, mais dans le contexte du raisonnement logique où il est établi que le MPP est une connaissance qui est toujours bien maîtrisée, obtenir 0.6 comme f1score pour la prédiction de réponses correctes n’est pas acceptable. C’est pourquoi nous avons gardé λ à 0.10. Cependant, la solution reste valable pour les données où le rapport « nombre de bonnes réponses/nombre de questions répondues » ou « nombre de mauvaises réponses/nombre de questions répondues » sur une compétence n’est pas trop bas (comme dans ce cas) et est inférieur à 0.5. Pour les connaissances difficiles à maîtriser (connaissances plafonds), il existe une différence significative entre le DKT et les autres modèles. Le DKT de base n’a pas été en mesure de prédire les bonnes réponses sur les connaissances difficiles à maîtriser. Ce comportement ne peut pas être toléré car le traçage des connaissances échouera pour les apprenants qui maîtrisent cette connaissance. Il est donc important de s’assurer que le modèle final soit précis pour toutes les connaissances. Sur les connaissances planchers/plafonds, on constate que le DKTm et le DKTm+BN se comportent mieux que le DKT, ce qui signifie que les changements que nous avons apportés au DKT original n’affectent pas sa capacité prédictive normale.

Ces résultats montrent que le DKT n’est pas en mesure de faire un traçage avec précision des connaissances planchers et plafonds, comparativement au DKTm et au DKTm+BN. Au cours de nos expériences, nous avons remarqué que, pour les connaissances très faciles à maîtriser, les 3 modèles n’ont pas été en mesure de tracer les réponses incorrectes, en raison du fait que le rapport « nombre de réponses incorrectes/nombre total des réponses aux questions » était très faible. Cependant, avec le modèle hybride, les résultats ont été notables. Nous avons fixé les valeurs des paramètres de régularisation, mais pour les travaux futurs nous prévoyons de faire une recherche par quadrillage (grid search) pour trouver les meilleures valeurs. Nous sommes également conscients que le manque de données pourrait biaiser les résultats obtenus puisque les architectures d’apprentissage profond fonctionnent mieux sur des ensembles de données plus importants. Cependant, le problème des connaissances plancher/plafond peut toujours survenir même avec un grand ensemble de données. Ainsi, nous pensons que les solutions que nous avons proposées peuvent fonctionner sur des ensembles de données plus importants.

5. Le module Tuteur de Muse-Logique

5.1. Objectif principal

L'objectif principal dans Muse-Logique est d'aider l'apprenant à devenir un bon raisonneur logique quelles que soient les situations de raisonnement. Muse-Logique Tuteur doit être en mesure de diagnostiquer la procédure mentale de raisonnement de l'apprenant pour détecter les erreurs de raisonnement et l'aider à les corriger. Pour ce faire, en collaboration avec les experts, nous avons précisé les interventions du tuteur lorsque des erreurs sont détectées ainsi que la façon dont le tuteur peut apporter son aide pour les corriger. Par exemple, dans un problème simple de syllogisme en situation concrète causale avec beaucoup d’alternatives (situation DCCMA), si l'apprenant décide de conclure à un problème invalide, le système doit vérifier si la réponse de l’apprenant vient du fait qu’il n’a pas examiné d'autres alternatives possibles de la situation mentionnée dans la prémisse. Si tel est le cas, le tuteur lui recommandera alors de penser à l’existence d’alternatives. Si l’apprenant refuse de conclure à un problème valide, le tuteur lui demandera la raison de cette réserve. Si sa réponse montre qu’il doute de la véracité de la prémisse majeure, le système lui rappellera l’importance de toujours considérer celle-ci comme pouvant être vraie.

Nous avons implémenté une base de telles règles d'intervention fournies par les experts logiciens pour chaque erreur possible suivant la situation (type de contenu) dans laquelle le raisonnement est opéré. En outre, l'un de nos objectifs était de mettre en place un soutien métacognitif à l'apprenant. Nous avons examiné attentivement les méta-structures logiques (pour la logique propositionnelle classique) comme décrit dans les sections précédentes et avons analysé la façon dont elles seront utilisées pour fournir une rétroaction visuelle à l'apprenant, afin qu'il ou elle soit consciente de ses propres erreurs de raisonnement.

5.2. Implémentation et intégration des composants validés

Muse-Logique offre quatre niveaux d’activités d'apprentissage pour l'apprenant, organisés en trois groupes de services d'apprentissage :

- Le service d'exploration du domaine qui utilise l’ontologie du domaine.

- Le service des exercices permettant à l’apprenant de résoudre une variété de problèmes de raisonnement incluant les syllogismes et les polysyllogismes, mais aussi des exercices généraux sur les concepts du raisonnement y compris la conversion de formules logiques dans des situations de raisonnement, la vérification de formules bien formées, la construction de table de vérité, etc. Ce service intègre un générateur automatique de problèmes (voir plus loin).

- L’espace de visualisation métacognitif du raisonnement qui offre entre autres la possibilité d’explorer l’état du réseau bayésien, et d’illustrer les erreurs par les méta-structures de la logique (treillis de Boole et groupes de Klein pour la logique propositionnelle), complété par un sous-espace d’autodiagnostic offert à l’apprenant et lui permettant de simuler son raisonnement à travers des structures sémantiques comme une table de vérité.

Selon cette dernière perspective, la figure 8 présente un cas d’erreur de raisonnement, avec l’intervention du Tuteur visant à ce que l’apprenant réalise lui-même l’erreur qu’il a commise, et ce par une simulation interactive de son raisonnement à travers une table de vérité.

Figure 8 • Exemple d’erreur de raisonnement d’un apprenant avec feedback du Tuteur

5.3. Gérer les erreurs de raisonnement dans Muse-Logique

Les erreurs systématiques en logique classique et en logique probabiliste sont identifiées dans la littérature ; les erreurs dans d'autres systèmes seront recueillies par des expériences. Dans Muse-Logique, les expériences sur les erreurs de raisonnement sont introduites à travers une variété d'activités de raisonnement, y compris syllogismes et polysyllogismes. Dans certains d'entre eux, l'apprenant suggère sa réponse en choisissant dans une liste (celle étant valide ou celle se rapportant aux erreurs de type 1), puis le système vérifie (grâce à Muse-Expert) si la réponse suggérée est logiquement valide ou non et fournit des commentaires pertinents après un diagnostic cognitif. Certaines questions offrent un temps de réponse limité de quelques secondes, de sorte que le caractère spontané des réponses de type 1 sera plus facilement déterminé. D'autres invitent les participants à décrire brièvement la procédure utilisée pour répondre, de sorte que cela peut aider pour l'interprétation des résultats et peut révéler des différences de procédure entre les réponses de type 1 et de type 2.

5.4. Génération automatique de problèmes de raisonnement

Les problèmes de raisonnement de type syllogismes et polysyllogismes sont des cas typiques de résolution de problème en raisonnement logique, car ils nécessitent la capacité de raisonner en conformité avec les règles d'inférence pertinentes pour trouver la solution (parvenir à une conclusion logiquement valide). Un syllogisme catégorique est composé de trois parties, la prémisse majeure, la mineure et la conclusion, par exemple :

- Prémisse majeure : « Je vais choisir la soupe ou je vais choisir la salade » ;

- Prémisse mineure : « Je ne vais pas choisir la soupe » ;

- Conclusion : « Je vais choisir la salade ».

Selon le type de l'opérateur utilisé dans la prémisse majeure, un syllogisme pourrait être disjonctif, implicatif ou d'incompatibilité, soit trois types de raisonnements. L'exemple précédent est un syllogisme disjonctif. Dans ces syllogismes, la prémisse majeure peut toujours être considérée comme un antécédent (A) lié à un conséquent (C) par un opérateur logique. En outre, la prémisse mineure est une déclaration spécifique, qui est soit une affirmation de A ou C, ou la négation de A ou C. Chaque cas correspond à une seule règle d'inférence. Par exemple, la règle d'inférence valide associée à un syllogisme est un modus ponens ponendo (MPP) sur le conjonctif conditionnel si la prémisse mineure est l'affirmation de A. Par ailleurs, la conclusion est soit l'affirmation ou la négation de la partie de la prémisse qui n’est pas utilisée dans la mineure. Sur cette base, la prémisse majeure est suffisante pour générer un problème de syllogisme. Donc, notre banque de problèmes contient un stock de prémisses majeures auquel on ajoute des alternatives éventuelles pour A ou C. Pour chaque problème de syllogisme, le système fournit à l'apprenant trois choix possibles. Les deux premiers choix sont l'affirmation et la négation de la partie de la prémisse majeure qui n’est pas présente dans la mineure. Le troisième choix est « Vous ne pouvez pas conclure ». Un de ces trois choix de réponses est toujours l'erreur spontanée typique de Type 1. Notre algorithme est capable de détecter automatiquement ce choix ainsi que la bonne réponse. Le système tient compte de l'évolution de l'étudiant dans ses apprentissages (état du réseau bayésien) et de la stratégie pédagogique en jeu (règles du tuteur sur l'enchaînement des questions) pour la génération du prochain problème. Les problèmes générés sont situés dans une des six classes de situations identifiées du tableau 1.

6. Conclusion

Le travail présenté dans cet article est issu d’une initiative multidisciplinaire qui nous a permis de nous inscrire dans une perspective de conception participative ayant mené à la co-construction d’un ensemble de composants validés par les experts du raisonnement logique et de la psychologie du raisonnement avant leur implémentation informatique. Cet article avait pour but de partager cette expérience avec le lecteur. Nous y avons présenté les éléments qui nous ont motivés à proposer un tel système, puis la démarche entreprise pour définir et expliciter les éléments de référence que nous avons utilisés. Nous avons donné un aperçu des différents modules et de leurs composants, en accordant une attention particulière à la construction d’un modèle apprenant prédictif hybride, fondé à la fois sur les données et sur les connaissances expertes. Nous avons décrit les différentes techniques d’apprentissage machine qui ont été développées dans cette perspective. Une première expérimentation a permis de collecter des données pour la construction de ce modèle prédictif comportant une composante psychométrique utilisée pour l’initialisation et la validation du réseau bayésien, un processus de traçage de connaissance bayésienne et un modèle d’apprentissage profond hybride qui lui confère une précision inférentielle améliorée. Les fonctionnalités du système MUSE-Logique ont ensuite été décrites et illustrées.

Muse-Logique est en cours de déploiement dans le cadre d’un cours de logique offert aux étudiants de première année à l’Université de Québec à Montréal. Ce déploiement nous permettra de collecter plus de données empiriques afin de mieux mesurer l’apport du système en termes de gain d’apprentissage, mais aussi, de disposer d’une plus grande quantité de données pour l’entraînement du modèle prédictif de l’apprenant.

À propos des auteurs

Roger Nkambou est professeur titulaire au département d'informatique de l'Université du Québec à Montréal (UQAM). Il est également directeur du Centre de Recherche en Intelligence Artificielle à la Faculté des Sciences de l’UQAM. Ses intérêts de recherche incluent les thèmes suivants : ingénierie des connaissances, ingénierie ontologique, ingénierie des systèmes intelligents, architectures d’agents cognitifs, fouille de données éducationnelles, apprentissage machine et systèmes tutoriels intelligents. Depuis plus d’une vingtaine d’années, il a mené plusieurs projets de recherche financés portant sur des sujets variés : l’élaboration de modèles d’agents artificiels affectifs dotés d’une intelligence émotionnelle (FRQNT, FRQSC), le développement de méthodes d’extraction de connaissances et d’ingénierie ontologique (CRSNG, Hydro-Québec), ou plus récemment, le développement de nouveaux algorithmes et modèles d’apprentissage profond pour la prédiction et la classification de comportements dans de contextes variés (CRSNG, FRQSC, BMU, Bombardier, CAE).

Adresse : Université du Québec à Montréal, 201 Avenue du Président-Kennedy, Montréal (Québec) Canada, QC H2X 3Y7

Courriel : nkambou.roger@uqam.ca

Toile : https://professeurs.uqam.ca/professeur/nkambou.roger/

Ange Adrienne Nyamen Tato est chercheure spécialiste en Intelligence artificielle pour Beam Me Up Augmented Intelligence et est également chercheure postdoctorale à l’Université du Québec à Montréal. Elle est spécialiste de technologies de l’éducation et d’intelligence artificielle. Ses recherches portent sur la modélisation automatique des comportements humains dans les systèmes intelligents et sur le développement d’architectures neuronales plus intelligentes. Elle travaille notamment sur des modèles neuronaux plus puissants en matière d’apprentissage et pouvant prendre en compte des connaissances expertes. Ces modèles sont aussi utilisés pour le traçage de comportements multimodaux d’usagers dans les systèmes.

Adresse : Université du Québec à Montréal, 201 Avenue du Président-Kennedy, Montréal (Québec) Canada, QC H2X 3Y7

Courriel : nyamen_tato.ange_adrienne@uqam.ca

Toile : https://www.linkedin.com/in/ange-adrienne-nyamen-tato-5a349480/

Janie Brisson est professeure adjointe au département d’éducation et pédagogie de l’Université du Québec à Montréal. Elle est spécialiste de psychologie cognitive, de logique et des technologies de l’éducation. Ses recherches portent sur les processus analytiques et intuitifs impliqués dans le raisonnement humain. Elle s’intéresse notamment au rôle du bagage de connaissances dans les biais de raisonnement ainsi qu’à l’automatisation des principes logico-mathématiques au sein du développement cognitif.

Adresse : Université du Québec à Montréal, 1205, rue Saint-Denis, Local: N-4900, Montréal (Québec) Canada, H2X 3R9

Courriel : brisson.janie@uqam.ca

Toile : https://www.linkedin.com/in/janie-brisson-775ab055/

Serge Robert est professeur titulaire au Département de philosophie de l’Université du Québec à Montréal. Il y dirige le Laboratoire d’Analyse Cognitive de l’Information, codirige l’équipe Muse Logique en systèmes tutoriels intelligents et participe à l’Institut des Sciences Cognitives et au Centre de Recherche en Intelligence Artificielle. Il est spécialiste de logique, de philosophie des sciences et de sciences cognitives. Ses travaux portent, depuis plus de 40 ans, sur le fonctionnement du raisonnement humain et sur son rôle dans la connaissance, dans la prise de décision et dans les domaines de l’intelligence artificielle et de l’éducation. Il travaille notamment à modéliser les procédures du raisonnement spontané et leurs fonctions cognitives, en les comparant avec le raisonnement scientifique.

Adresse : Université du Québec à Montréal, Département de philosophie, Case postale 8888, Succursale Centre-ville, Montréal (Québec) Canada, H3C 3P8.

Courriel : robert.serge@uqam.ca

Toile : https://professeurs.uqam.ca/professeur/robert.serge/

Maxime Sainte-Marie est chercheur postdoctoral au Danish Centre for Studies in Research and Research Policy de l'Université d'Aarhus, au Danemark. Titulaire d’un doctorat en informatique cognitive de l’Université du Québec à Montréal, il est également professeur invité au Centre interuniversitaire de recherche sur la science et la technologie.

Adresse : The Danish Centre for Studies in Research and Research Policy, Department of Political Science, Aarhus University, Bartholins Allé 7, DK–8000 Aarhus C, Denmark

Courriel : msaintemarie@gmail.com

Toile : https://crc.ebsi.umontreal.ca/equipe/maxime-sainte-marie/

RÉFÉRENCES

Almond, R. G., DiBello, L. V., Moulder, B. et Zapata-Rivera, J. D. (2007). Modeling diagnostic assessments with Bayesian networks. Journal of Educational Measurement, 44, 341–359.

Barnes, T., et Stamper, J. (2010). Automatic hint generation for logic proof tutoring using historical data. Educational Technology & Society, 13(1), 3–12.

Beck, J. E. et Chang, K.-M. (2007). Identifiability: A fundamental problem of student modeling. Dans Proceedings of the International Conference on User Modeling (p.137–146). Springer.

Brisson, J., de Chantal, P-L., Lortie-Forgues, H. et Markovits, H (2014). Belief bias is stronger when reasoning is more difficult. Thinking & Reasoning 20(3), 37-41.

Chen, J., de la Torre, J. et Zhang, Z. (2013). Relative and absolute fit evaluation in cognitive diagnosis modeling. Journal of Educational Measurement, 50(2), 123-140.

Chen, Y., Yang, Z., Xie, Y. et Wang, Z. (2018). Contrastive learning from pairwise measurements. Dans Proceedings of the 32nd Conference on Neural Information Processing Systems (NeurIPS 2018). NY, United States : Red Hook.

Cloutier, A. (2016). Métacognition, raisonnement logique et philosophie pour enfants [mémoire de maîtrise, Université du Québec à Montréal, Canada].

Corbett, A. T. et Anderson, J. R. (1994). Knowledge tracing: Modeling the acquisition of procedural knowledge. User modeling and user-adapted interaction, 4(4), 253–278.

Cosmides, L. (1989). The logic of social exchange: Has natural selection shaped how humans reason? Studies with the Wason selection task. Cognition, 31(3), 187-276.

de la Torre, J. (2009). DINA model and parameter estimation: A didactic. Journal of Educational and Behavioral Statistics, 34(1), 115–30.

de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76, 179–199 (2011).

Dennett D. (2003). Freedom Evolves. Viking Press.

Espino, O. et Byrne, R.M.J. (2020). The suppression of inferences from counterfactual conditionals. Cognitive Science, 44.

Evans, J.S.B.T., Newstead, S.E. et Byrne, R.M.J. (1993). Human Reasoning: The psychology of deduction. Hove, UK : Lawrence Erlbaum.

Evans, J. S. B. (2002). Logic and human reasoning: an assessment of the deduction paradigm. Psychological Bulletin 128(6), 978-996.

Girotto, V., Gilly, M., Blaye, A. et Light, P. (1989). Children's performance in the selection task: Plausibility and familiarity. British Journal of Psychology, 80(1), 79-95.

Groß, J., Robitzsch, A. et George, A. C. (2016). Cognitive diagnosis models for baseline testing of educational standards in math. Journal of Applied Statistics, 43(1), 229-243.

Guilford, J. P. et Lyons, T. C. (1942). On determining the reliability and significance of a tetrachoric coefficient of correlation. Psychometrika, 7(4), 243-249.

Houdé, O. (2019). 3-System theory of the cognitive brain: A post-piagetian approach to cognitive development. Abingdon, UK : Routledge.

Houdé, O. (2000). Inhibition and cognitive development: Object, number, categorization, and reasoning. Cognitive Development, 15, 63-73.

Kasurinen, J. et Nikula, U. (2009). Estimating programming knowledge with bayesian knowledge tracing. ACM SIGCSE Bulletin, 41, 313–317.

Khajah, M., Lindsey, R. V. et Mozer, M. C. (2016). How deep is knowledge tracing? Dans Proceedings of the 9th International Conference on Educational Data Mining (p. 94-101).

Lesta, L. et K. Yacef (2002). An intelligent teaching-assistant system for Logic. Dans S. Cerri, G. Gouardères et F. Paraguaçu (dir.), Proceedings of the 6th International Conference ITS 2002 (p.421-431). Springer-Verlag.

Markovits, H. (2014). On the road toward formal reasoning: Reasoning with factual causal and contrary-to-fact causal premises during early adolescence. Disponible sur internet, 128, 37-51.

Markovits, H., Brunet, M.-L., Thompson, V. et Brisson, J. (2013). Direct evidence for a dual process model of deductive inference. Journal of Experimental Psychology: Learning, Memory, and Cognition, 39(4), 1213-1222.

Mercier, H., Boudry, M., Paglieri, F. et Trouche, E. (2017). Natural-born arguers: Teaching how to make the best of our reasoning abilities. Educational Psychologist, 52(1), 1-16.

Moshman, D. (2004). From inference to reasoning: The construction of rationality. Thinking & Reasoning, 10(2), 221–239.

Nkambou, R., Mizoguchi, R. et Bourdeau, J. (dir.). (2010). Advances in Intelligent Tutoring Systems. Berlin Heidelberg : Springer.

Piech, C., Bassen, J., Huang, J., Ganguli, S., Sahami, M., Guibas, L.-J. et Sohl-Dickstein, J. (2015). Deep knowledge tracing. Dans Proceedings of Advances in neural information processing systems (NIPS 2015), 505–513.

Robert, S. (2005). Categorization, reasoning and memory. Dans H.Cohen, et C. Lefebvre (dir.), Handbook of Categorization in Cognitive Science (p. 699-717). Elsevier Science.

Robert, S. et Brisson, J. (2016). The Klein Group, Squares of Opposition and the Explanation of Fallacies in Reasoning. Logica Universalis 10(2-3), 377-389.

Rossi, S. et van der Henst, J. B. (dir.). (2007). Psychologies du raisonnement. Bruxelles : DeBoeck.

Rupp, A., Templin, J. et Henson, R. (2010). Diagnostic measurement: Theory, methods and applications. New York : Guilford Press.

Stanovich, K. E. (2011). Rationality and the reflexive mind. Oxford Univ. Press.

Tato, A. et Nkambou, R. (2019). Some Improvements of Deep Knowledge Tracing. Dans Proceedings of the IEEE 31st International Conference on Tools with Artificial Intelligence (ICTAI) (p. 1460-1464). IEEE Computer Society.

Tato, A. et Nkambou, R. (2020). Improving First-Order Optimization Algorithms (Student Abstract). Dans Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence (p. 13935-13936).

Tchetagni, J., Nkambou, R. et Bourdeau, J. (2007). Explicit Reflection in Prolog-Tutor. International Journal on Artificial Intelligence in Education, 17(2), 169-215. Disponible sur internet.

Varin, C. (2007). L’Enseignement du raisonnement conditionnel : de la logique aux neurosciences [mémoire de maîtrise, Université du Québec à Montréal, Canada].

Yudelson, M. V., Koedinger, K. R. et Gordon, G. J. (2013). Individualized Bayesian knowledge tracing models. Dans Proceedings of the International Conference on Artificial Intelligence in Education (AIED 2013) (p. 171–180).

ANNEXE

Figure A1 • Heatmap illustrant la prédiction du DKT original sur le même apprenant

Figure A2 • Heatmap illustrant la prédiction du DKTm sur le même apprenant

Figure A3 • Heatmap illustrant la prédiction du DKTm+BN sur le même apprenant

¹ Le vecteur e rend compte de l’état des connaissances de l’apprenant tel que prédit par les experts, obtenu par inférence bayésienne sur le réseau bayésien initial (construit par les experts du domaine).

Référence de l'article :

Roger NKAMBOU, Ange TATO, Janie BRISSON, Serge ROBERT, Maxime SAINTE-MARIE, Une approche hybride à la modélisation de l’apprenant dans un STI pour l’apprentissage du raisonnement logique, Revue STICEF, Volume 27, numéro 2, 2020, DOI:10.23709/sticef.27.2.5, ISSN : 1764-7223, mis en ligne le 04/06/2021, http://sticef.org