 Sciences et Technologies
Sciences et Technologiesde l´Information et
de la Communication pour
l´Éducation et la Formation
version à télécharger (pdf)
Volume 17, 2010
Article de recherche
|
Contact : infos@sticef.org |
Aide à l'évaluation diagnostique de travaux pratiques en
électronique numérique en utilisant un algorithme
d'apprentissage
|
|
|
|
|
|
|
1. Introduction
L’électronique numérique est l’un des cours dispensés en premier cycle ou en début de second cycle des écoles d’ingénieurs. Ce cours a pour objectif de présenter aux étudiants comment sont construits les éléments de base d’un ordinateur à partir des composants très simples que sont les portes logiques « et », « ou », « non », etc. En plus des cours magistraux et des travaux dirigés sur papier, les étudiants valident leurs connaissances à l’aide des travaux pratiques (TP), en construisant des circuits électroniques permettant par exemple de réaliser des additions de bits (appelés « additionneur »), des soustractions de bits (appelés « soustracteur ») ou encore de calculer des compléments à deux. Il y a encore quelques années, ces TP étaient uniquement réalisés avec de vrais composants électroniques (figure 1(a)), alors qu’aujourd’hui, ils sont souvent réalisés à l’aide de simulateurs (figure 1(b)).
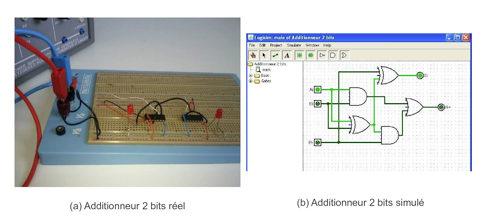
Figure 1 • Deux Additionneurs
À l’ENSA de Tanger, c’est le logiciel open-source LogiSim (http://ozark.hendrix.edu/~burch/logisim/) qui est utilisé pour les TP d’électronique numérique. De plus, afin de faciliter la gestion de ces TP et leur correction, la plate-forme TEB, pour « Travaux pratiques d’Électronique Binaire », a été développée (figure 2). Cette plate-forme permet aux enseignants de mettre en ligne des exercices, ainsi que de récupérer et d’évaluer les schémas électroniques (SE) des apprenants. Toutefois, la correction de ces schémas est un travail délicat et fastidieux. En effet, outre le fait que le nombre de schémas à corriger est élevé, la correction d’un SE est une tâche difficile car il n’existe pas une solution unique, un SE est la concrétisation de toute une démarche méthodologique.
Ceci définit notre problématique : construire un système d’aide à la correction de SE simples. Il aura pour but d’aider l’enseignant à donner une note à la production de l’apprenant, ce qui correspond à une évaluation sommative. Mais il permettra aussi de justifier cette note afin que l’apprenant comprenne l’origine de ses erreurs, d’où une évaluation diagnostique (cette aide pouvant intervenir indépendamment du « pourquoi » et du « quand » l’enseignant décide d’évaluer l’apprenant).

Figure 2 • L’interface de la plate-forme TEB
Pour résoudre ce problème applicatif, nous nous donnons comme objectif de satisfaire deux contraintes a priori antagonistes. D’une part, nous voulons spécifier à la conception de notre système peu de connaissances afin d’être le plus généraliste possible. D’autre part, nous voulons aussi minimiser l’apport de connaissances à la création de chaque exercice, afin de ne pas alourdir la tâche de l’enseignant.
La première contrainte écarte de fait l’approche la plus souvent rencontrée, c’est-à-dire celle où les connaissances du domaine et les connaissances didactiques sont explicitement représentées. Ces systèmes sont très spécifiques aussi bien du point de vue thématique que du point de vue du niveau des connaissances à évaluer.
Une autre voie est apparue depuis quelques années, entre autres présentée dans les travaux de thèse de F. Delorme (Delorme, 2005). Il a en effet proposé d’utiliser des algorithmes de classification pour évaluer des cartes conceptuelles d’apprenants exprimant des définitions, donc un « savoir », en informatique (plus précisément en algorithmique et en informatique répartie). Les connaissances du domaine et les connaissances didactiques ne sont alors plus explicitement représentées, mais elles sont embarquées au sein des solutions des exercices et dans une mesure de similarité entre ces solutions et les productions d’apprenants.
Bien que notre domaine d’application soit différent, nous faisons l’hypothèse que ces mêmes techniques vont nous permettre d’évaluer le « savoir-faire », en atteignant notre objectif.
Nous commencerons donc par présenter plus en détail notre domaine d’application en insistant sur le fait que produire un SE est une démarche complexe. Dans cette même partie, nous présenterons les données expérimentales qui nous permettront par la suite de valider nos hypothèses. Nous rappellerons aussi le principe et les caractéristiques des algorithmes de classification et comment en sélectionner un qui répond à notre problématique. Nous présenterons ensuite une mesure de similarité entre SE, et nous montrerons que cette dernière permet de faire de l’évaluation sommative. Enfin, avant la conclusion et quelques perspectives, nous montrerons que l’utilisation de l’algorithme du k-ppv associé à une base d’apprentissage construite manuellement puis automatiquement permet de faire de l’évaluation diagnostique.
2. Contexte
2.1. Domaine d'application
2.1.1. Schéma électronique
Un schéma électronique est la représentation graphique d’un circuit logique réalisant une ou plusieurs fonctions. Ce circuit est composé d’un ensemble de portes logiques interconnectées entre elles.
Une porte logique est un circuit électronique élémentaire réalisant une opération simple. Elle peut être constituée de plusieurs entrées et une seule sortie. Il existe des portes logiques de base (not, qui représente la négation ; and, qui représente le et logique ; or, qui représente le ou logique) et des portes logiques composées, construites à partir d’une combinaison des trois portes logiques de base (nand, qui représente la négation du et logique ; nor, qui représente la négation du ou logique ; xor, qui représente le ou exclusif ; nxor, qui représente la négation du ou exclusif).
Un circuit logique « combinatoire » (figure 3) est un circuit logique qui possède n entrées Ei(1≤i≤n) et m sorties Sj(1≤j≤m), de telle sorte que Sj = fj(E1,...,En). fj étant la fonction logique correspondant à la sortie Sj du circuit, elle dépend uniquement de l’état des entrées Ei.

Figure 3 • Modèle d’un circuit logique combinatoire
Les fonctions logiques de base sont issues des mathématiques théoriques de l’algèbre de Boole, qui est une méthode mathématique déductive créée par le mathématicien anglais George Boole dans son ouvrage The Laws of Thought (Boole, 1854). L’algèbre de Boole permet de traduire des signaux électriques en expressions mathématiques plus faciles à manipuler par les informaticiens.
Les variables de l’algèbre booléenne, appelées variables logiques, ne peuvent avoir qu’une des deux valeurs 0 ou 1. Elles peuvent être réunies à l’aide des opérateurs élémentaires pour former des expressions algébriques.
Les fonctions logiques sont donc représentées algébriquement à l’aide d’expressions construites à partir des opérateurs élémentaires {not,and,or} (Nketsa, 1998) ou des opérateurs composés {nand,nor,xor,nxor}. En dehors de cette représentation algébrique, il existe d’autres méthodes permettant de les représenter :
- La table de vérité est un tableau renseignant les états de chaque sortie en fonction de tous les états possibles des entrées. Chaque table de vérité correspond à une et une seule fonction logique.
- La table de Karnaugh, du nom de son inventeur (Karnaugh, 1953), est un outil graphique semblable à la table de vérité. C’est un tableau de deux dimensions comportant 2n cases, où n est le nombre d’entrées. Chaque case du tableau correspond à une ligne de la table de vérité (Nketsa, 1998). Ce mode de représentation est humainement interprétable avec cinq ou six variables d’entrée au maximum. Il est surtout utile pédagogiquement pour s’initier aux circuits logiques (Karnaugh, 1953).
- Le logigramme est un schéma graphique normalisé illustrant l’expression d’une fonction logique sans tenir compte des constituants technologiques. C’est à la fois une représentation graphique et symbolique qui s’effectue à l’aide des représentations symboliques des opérateurs logiques reliés entre eux. Un logigramme est l’aboutissement final qui permettra de construire techniquement le SE étudié.
Dès que nous disposons de l’expression algébrique d’une fonction logique, si elle n’est pas minimale, il est possible de la simplifier pour obtenir une expression comportant moins de termes ou moins de variables par terme. Cette nouvelle équation peut alors servir de modèle pour construire le SE correspondant à la fonction logique, mais qui requiert moins de portes logiques. La simplification d’une expression algébrique n’est pas évidente car il peut y avoir plusieurs solutions possibles. Une fonction logique peut donc être représentée par plusieurs expressions algébriques différentes mais totalement équivalentes.
2.1.2. Synthèse d’un circuit logique
La synthèse d’un circuit logique a pour but la réalisation d’un SE d’une fonction logique répondant à des spécifications particulières. Lors de cette synthèse, il est souhaitable d’obtenir l’expression algébrique équivalente qui produira un circuit de taille minimale (Zanella et Ligier, 1998).
Il peut y avoir plusieurs solutions possibles, toutes aussi « justes » les unes que les autres. En revanche, si nous nous basons sur certains critères (nombre de portes, nombre de connexions, degré de simplification de l’expression logique, etc.), ces solutions peuvent être classées les unes par rapport aux autres.
La démarche pédagogique classique pour faire la synthèse d’un circuit logique combinatoire est la suivante (Zanella et Ligier, 1998) :
- définir le nombre des entrées et sorties du circuit à partir de l’énoncé ;
- construire la table de vérité à partir de la définition du circuit ;
- déduire une expression algébrique du circuit à l’aide des méthodes de simplification : table de Karnaugh, lois de l’algèbre de Boole. Ceci consiste à obtenir une expression avec le minimum d’opérateurs logiques, afin de réduire le « coût » d’implémentation du circuit ;
- réaliser le SE à l’aide des différents opérateurs : not, and, or, nand, nor, xor ou nxor.
Le schéma obtenu est optimisé si la fonction logique correspondante a été simplifiée au maximum. Il peut exister plusieurs solutions suivant le degré et la démarche de simplification.
2.2. Données expérimentales
Un exemple de synthèse d’un circuit logique est l’exercice sur la réalisation d’un « additionneur binaire avec retenue ». C’est un exercice typique et simple, dont la finalité pédagogique est de comprendre comment un ordinateur effectue certaines opérations de base. L’énoncé de cet exercice est le suivant :
« L’additionneur binaire avec retenue est un circuit effectuant la somme Si de deux bits Ai et Bi d’ordre i et d’une retenue Ri-1 d’ordre i-1 immédiatement inférieur. Effectuez la synthèse d’un tel circuit en utilisant, dans la mesure du possible, les opérateurs logiques xor ou nxor. »
Ce circuit dispose de trois entrées (les deux bits à additionner Ai et Bi, et le bit de retenue de l’opération précédente Ri-1) et de deux sorties (Si la somme des deux bits et de la retenue précédente, et Ri la nouvelle retenue générée par la somme). Sa table de vérité est la suivante :
Tableau 1 • Table de vérité de l’additionneur avec retenue
Après simplification par la méthode de Karnaugh et utilisation des opérateurs composés comme demandé dans l’énoncé, les expressions algébriques simplifiées des deux sorties sont les suivantes :
Si = Ai ⊕ Bi ⊕ Ri-1
Ri = Ri-1.(Ai ⊕ Bi) + Ai.Bi
Finalement, le SE attendu pour cet exercice est présenté par la figure 4.
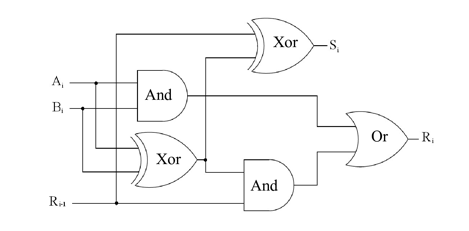
Figure 4 • Modèle d’un circuit logique combinatoire
Deux autres exercices de base : le soustracteur binaire avec retenue (trois entrées et deux sorties) et le complément à 2 (quatre entrées et quatre sorties), ont été aussi utilisés comme données expérimentales. Nous avons ainsi récupéré les résultats de travaux dirigés et examens corrigés de plusieurs promotions d’élèves ingénieurs pour ces exercices (il s’agit de 64 circuits d’apprenants pour l’additionneur, 62 circuits pour le soustracteur et 16 circuits pour le complément à 2). Nous avons ensuite synthétisé les « corrections manuelles » de l’enseignant, dont un extrait est donné par le tableau 2 contenant le détail de chaque étape de la synthèse du circuit logique de l’additionneur.
Tableau 2• Extrait du tableau de synthèse des corrections manuelles pour l’additionneur binaire avec retenue
3. Algorithmes d’apprentissage et évaluation
Les méthodes de classification sont issues des recherches en apprentissage automatique (Machine Learning en anglais) (Mitchell, 1997). L’objectif général de ces méthodes est d’associer des données à des classes, c’est-à-dire, attribuer à chaque donnée une étiquette qui représente une classe. Il existe deux grandes approches : l’apprentissage « supervisé » et l’apprentissage « non-supervisé ».
3.1. L’apprentissage supervisé
Dans la classification supervisée, les classes sont connues a priori. L’objectif est alors de déterminer la classe de toute nouvelle donnée en fonction de données (exemples) préalablement étiquetées (ces exemples forment la base d’apprentissage).
Il y a deux étapes dans la classification supervisée. La première, nommée phase d’apprentissage, étudie les données de la base d’apprentissage afin de trouver des caractéristiques qui permettent de discriminer les données en fonction de leur classe. La seconde phase, nommée phase de classification, attribue à chaque nouvelle donnée non étiquetée une classe d’appartenance.
Il existe de nombreuses techniques de classification supervisée, entre autres (Duda et al., 2001):
- les k plus proches voisins ;
- les réseaux bayésiens naïfs ;
- les réseaux de neurones ;
- les Séparateurs à Vaste Marge, nommés aussi Algorithme à Vecteurs Supports, Support Vector Machine en anglais (Vapnik, 1998) ;
- les arbres de décisions ;
- la programmation génétique.
3.2. L’apprentissage non supervisé
Dans la classification non-supervisée, aussi appelée segmentation (clustering en anglais), les classes ne sont pas connues a priori. L’objectif est alors d’associer un ensemble de données à différentes classes. Ce nombre de classes peut être un paramètre de l’algorithme.
Il existe aussi de nombreuses techniques pour la classification non-supervisée, comme par exemple la méthode des K-moyennes, K-means en anglais, ou encore les cartes de Kohonen, aussi appelée cartes auto-organisatrices ou Self Organizing Maps en anglais (Kohonen, 1982).
3.3. Évaluer l’apprenant avec un algorithme d’apprentissage
Notre hypothèse est que les algorithmes d’apprentissage vont nous permettre d’évaluer le savoir-faire. Or, évaluer c’est entre autres caractériser la production d’un apprenant, c’est-à-dire associer la production de l’apprenant à une information d’évaluation. Dans notre cadre, il s’agit donc d’utiliser des algorithmes d’apprentissage supervisé pour faire de l’évaluation.
En apprentissage supervisé, il n’existe pas d’algorithme qui soit supérieur aux autres. Ils ont tous leurs avantages et leurs inconvénients, mais selon le type de données qui sont traitées, certains sont plus adaptés que d’autres. Par exemple, dans les réseaux bayésiens naïfs, les réseaux de neurones, les arbres de décision ou la programmation génétique, les données sont souvent représentées sous forme d’une liste d’attributs (très souvent ces données sont des vecteurs de ℜn), alors que l’algorithme des k plus proches voisins ou l’algorithme à vecteurs supports requiert uniquement l’existence d’une mesure de similarité, ou mieux, de distance entre les données (on les nomme les « méthodes à noyaux »).
Généralement, les productions des apprenants ne peuvent être représentées par une liste d’attributs sans perte d’information importante. Par contre, il est envisageable de créer une mesure de similarité entre elles. Dès lors, les méthodes à noyaux semblent les algorithmes d’apprentissage les plus adaptés pour effectuer cette évaluation. Mais comment choisir entre l’algorithme du k-ppv et du SVM ?
Le principe de l’algorithme du k-ppv est assez simple puisqu’il n’y a pas de phase d’apprentissage à proprement parler et que la phase de décision se résume à choisir la classe d’une nouvelle donnée comme étant la classe la plus représentée parmi les k plus proches voisins. Par exemple, la figure 5 montre comment classer quatre nouvelles données (cercles blancs) à partir d’une base d’apprentissage composée d’éléments de trois classes (représentées par les cercles bleus, losanges verts et triangles rouges).
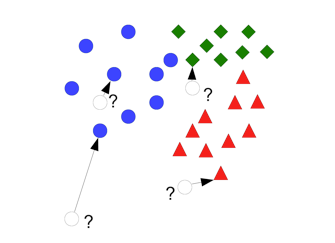
Figure 5• Principe de l’algorithme du k-ppv avec k = 1 (1–ppv)
L’algorithme à vecteurs supports, quant à lui, permet d’attribuer la classe d’un nouvel élément en fonction de sa position par rapport à une frontière (figure 6(a)). Cette frontière est calculée pendant la phase d’apprentissage en essayant de maximiser ses deux marges (figure 6(c)).
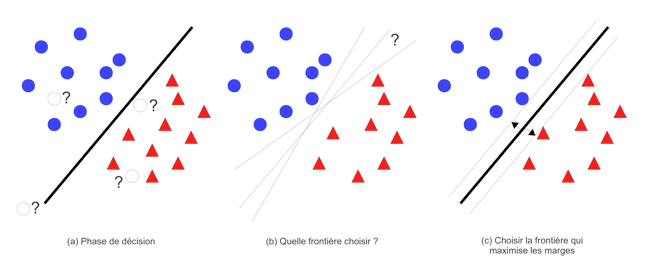
Figure 6• Phase d’apprentissage du SVM
Nous pouvons alors faire les constats suivants :
- la phase de décision du SVM est beaucoup plus efficace que celle du k-ppv puisque pour le SVM, il suffit de savoir de quel côté de la frontière se trouve la nouvelle donnée pour décider de sa classe, alors que pour le k-ppv, il faut calculer la distance entre la nouvelle donnée et tous les exemples de la base d’apprentissage. Le SVM sera donc privilégié pour de très grandes bases d’apprentissage ;
- initialement, le SVM ne permet de gérer que deux classes dans la base d’apprentissage, bien que la combinaison de plusieurs SVM associée à une stratégie « un contre tous » ou « un contre un » permette de faire de la classification multi-classes (Canu, 2007) ;
- le k-ppv permet de faire facilement du rejet par distance, c’est-à-dire que l’algorithme est capable d’indiquer le fait qu’il ne peut pas classer une nouvelle donnée car trop éloignée des exemples de la base d’apprentissage (c’est le cas par exemple de la donnée à classer en bas à gauche de la figure 5). Le SVM quant à lui, est incapable de le faire (sauf en utilisant une combinaison de plusieurs SVM permettant de faire de la classification « one-class » (Schölkopf et al., 2000)).
Au vue de ces remarques, le k-ppv semble à privilégier dans des systèmes d’évaluation, car dans ce contexte, le nombre d’exemples dans la base d’apprentissage est souvent faible (au maximum quelques centaines d’exemples). De plus, il faut absolument que le système d’évaluation puisse faire du rejet par distance afin d’indiquer à l’enseignant qu’il ne peut pas évaluer une production d’un apprenant lorsqu’elle se trouve au delà d’une certaine distance de tous les exemples de la base d’apprentissage.
Il nous faut donc maintenant définir une mesure de similarité entre SE.
4. Une mesure de similarité comme outil d’évaluation sommative
4.1. Un SE vu comme un ensemble de graphes
L’étude du SE présenté par la figure 4 montre qu’un SE peut être représenté par un graphe. De plus, dans notre contexte pédagogique, les SE ne peuvent pas avoir de « contre-réactions » (ce sont des SE simples, en boucle ouverte, sans cycle), ils peuvent donc être représentés par des graphes acycliques. Enfin, les sorties étant définies comme uniquement fonction des entrées, un SE peut être représenté par un ensemble de graphes acycliques (un graphe par sortie du SE).
Par exemple, le SE présenté par la figure 4 peut être formalisé par un ensemble de deux graphes acycliques présentés par la figure 7.
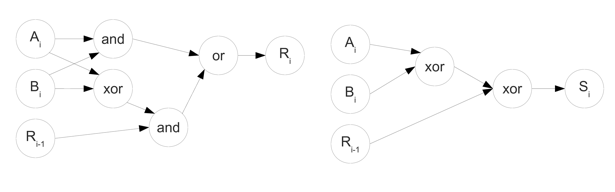
Figure 7• Représentation du SE « additionneur » à l’aide d’un ensemble de graphes acycliques
4.2. Mesures de similarité entre graphes
Dans (Bunke et Allerman, 1983), (Messmer et Bunke, 1998), (Neuhaus et al., 2006), et (Riesen et Bunke, 2008), Bunke propose plusieurs algorithmes de mesure de similarité basés sur la distance d’édition de graphes ou « Graph Edit Distance (GED) ». Le principe de ces algorithmes est le suivant : étant donnés deux graphes g1 et g2, l’idée est d’appliquer une séquence de transformations (ou d’opérations d’édition) sur g1 (insertion, substitution et suppression de sommets ou d’arcs) pour finalement transformer g1 en g2. Ce processus tend à déformer le modèle du graphe initial jusqu’à ce qu’il s’identifie avec le modèle de l’autre graphe.
Chaque transformation ayant un coût prédéfini (Bunke et Allerman, 1983), le coût d’une séquence de transformations est égal à la somme pondérée des coûts de chaque transformation. La séquence de transformations qui obtient un coût minimal représente la distance d’édition entre les deux graphes (Bunke, 1997) :
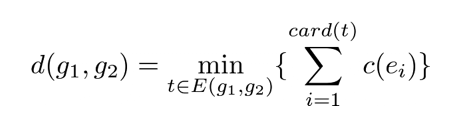
ei est appelé une opération d’édition. t = (e1,....ek) est une séquence d’opérations d’édition transformant g1 en g2, aussi appelée « chemin d’édition complet ». E(g1,g2) est l’ensemble des séquences d’opérations d’édition qui permettent de transformer g1 en g2. c est la fonction qui assigne un coût à une opération d’édition e.
Il existe six types de transformations possibles auxquelles sont associées un coût :
- Substitution de sommet : cette opération correspond au remplacement d’un sommet par un autre. Le coût de cette opération correspond au coût de remplacement entre les deux étiquettes des deux sommets ;
- Suppression de sommet : cette opération correspond à la suppression d’un sommet et de tous les arcs le reliant aux sommets adjacents. Le coût total de cette opération est égal au coût de suppression d’un sommet, plus les coûts de suppression de tous les arcs incidents à ce sommet ;
- Insertion de sommet : cette opération correspond à l’ajout d’un sommet et éventuellement des arcs le reliant aux autres sommets. Le coût total de cette opération est égal au coût d’insertion d’un sommet, plus les coûts d’insertion de tous les arcs incidents insérés ;
- Substitution d’arc : cette opération correspond au remplacement d’un arc par un autre. Le coût de cette opération correspond au coût de remplacement entre les deux étiquettes des deux arcs ;
- Suppression d’arc : cette opération correspond à la suppression d’un arc reliant deux sommets.
- Insertion d’arc : cette opération correspond à l’ajout d’un arc entre deux sommets.
Généralement, les algorithmes de « distance d’édition de graphes » utilisent une méthode de recherche basée sur A* qui « est un algorithme de recherche de chemin dans un graphe entre un nœud initial et un nœud final. Il utilise une évaluation heuristique sur chaque nœud pour estimer le meilleur chemin y passant, et visite ensuite les nœuds par ordre de cette évaluation heuristique... L’algorithme A* a été créé pour que la première solution trouvée soit l’une des meilleures » (Wikipedia). L’idée est donc de représenter le problème d’appariement de graphe par un arbre de recherche construit dynamiquement de façon itérative, dont la racine est l’état initial, les nœuds intermédiaires représentent des solutions partielles et les feuilles sont des solutions complètes.
Ce sont des algorithmes admissibles, en ce sens qu’ils garantissent de trouver un « appariement inexact optimal » entre les deux graphes (Nilsson, 1980). Cependant, de par leur complexité, ils ne peuvent fonctionner que sur des graphes relativement petits. En revanche, afin de réduire le temps et la complexité d’exécution, ces algorithmes utilisent diverses techniques heuristiques qui sont souvent dépendantes du domaine d’application.
4.3. Proposition d’une mesure de similarité entre schémas électroniques
Au vue des deux parties précédentes, il est donc possible de définir une mesure de similarité entre SE. Mais nous savons aussi que les algorithmes GED, basés sur l’algorithme A*, peuvent être optimisés à l’aide d’heuristiques. Étudions donc les particularités des SE pour identifier ces heuristiques.
4.3.1. Schémas électroniques équivalents
La notion d’équivalence entre SE se base sur les théorèmes et lois de l’algèbre booléenne (Darche, 2002) et (Zanella et Ligier, 1998). En effet, les deux lois représentées par les opérateurs and et or sont commutatives et associatives, et la transformation d’une expression algébrique en un SE peut avoir plusieurs résultats graphiquement différents, mais équivalents vis-à-vis de la fonction logique correspondante. Ceci est généralement dû à l’arité variable de certains composants électroniques.
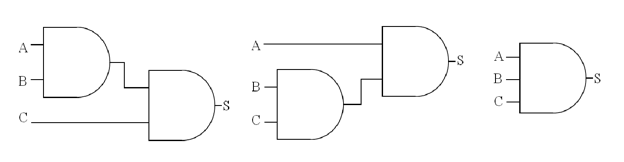
Figure 8• Exemple de schémas électroniques équivalents
Par exemple, les schémas électroniques de la figure 8 correspondent à la même fonction logique (S = A.B.C), et sont donc « équivalents », même si leurs représentations graphiques sont différentes. Cette différence est due à l’utilisation de portes logiques d’arité 2 dans les deux premiers schémas et de porte logique d’arité 3 dans le dernier schéma.
La distance d’édition de graphes entre ces schémas, considérés comme des graphes, telle qu’elle a été définie par l’algorithme de Bunke et al., n’est pas égale à zéro. Du point de vue structurel, ces schémas ne sont donc pas identiques. Ceci pourrait « fausser » le résultat des mesures de similarité entre SE si nous ne tenions pas compte de cette particularité d’équivalence.
Pour cela, nous allons introduire la notion d’équivalence entre SE dans la construction de notre mesure de similarité, en maximisant à chaque fois l’arité des composants électroniques. Ainsi, dans l’algorithme GED, ce n’est plus l’égalité entre deux SE qui est utilisée pour savoir si un nœud de l’arbre de recherche est une feuille, mais l’équivalence.
4.3.2. Type de composants
Une autre particularité des circuits électroniques est la différenciation entre les portes logiques. En effet, une porte logique peut représenter une « entrée », une « sortie » ou un autre « composant logique », par exemple : and, or, xor, etc. Nous allons donc introduire la notion de « type » pour les portes logiques, ce qui nous permettra de n’effectuer que les transformations d’un composant par un autre composant du même type :
- la valeur Entrée pour les portes logiques de type « entrée » ;
- la valeur Sortie pour les portes logiques de type « sortie » ;
- la valeur PorteLogique pour les autres portes logiques.
4.3.3. Algorithme de mesure de similarité entre schémas électroniques
Pour l’élaboration de notre algorithme de mesure de similarité entre SE (algorithme 1), nous nous sommes donc basés sur les éléments suivants :
- l’algorithme de la distance d’édition entre graphes présenté précédemment ;
- la notion d’équivalence entre schémas électroniques (fonction schémas_Électroniques_Équivalents) ;
- le coût d’une succession de transformations (fonction c) ;
- la notion de « type » pour les composants logiques (fonction typeCL).
Cet algorithme 1 explore toutes les possibilités de correspondances entre les composants logiques du schéma électronique SE1 (ligne 1) par rapports aux composants logiques du schéma électronique SE2 (ligne 2). La substitution d’un composant logique par un autre est notée : u → v, l’insertion d’un composant est notée : ε → v et la suppression u → ε. Un composant logique peut très bien être substitué par un autre composant identique, cela correspond à un coût de transformation égal à zéro.
AR contient la construction dynamique de l’arbre de recherche contenant les différentes séquences de transformations. Initialement, AR est vide (ligne 3). Ensuite, toutes les opérations possibles de substitution et suppression de composants logiques sont générées simultanément pour le premier composant logique de SE1 par rapport à tous les composants logiques de SE2 de même type (lignes 4-9).
À chaque itération, un SE1bis est construit à partir de la première séquence de transformations de AR ayant un coût minimal : pmin (lignes 10-13). Si les deux schémas SE1bis et SE2 sont équivalents (ligne 27), la mesure de similarité entre les deux schémas est retournée, sinon (ligne 14), de nouvelles opérations de substitution et de suppression de composants logiques sont générées dans l’arbre AR pour le composant logique suivant du schéma SE1 par rapport aux composants logiques de SE2 de même type, non encore traités (lignes 15-22). Si tous les composants logiques de SE1 ont été traités, le reste des composants logiques de SE2 sont insérés dans AR en une seule opération (ligne 24).
4.4. Validation expérimentale
Le choix des valeurs pour les coûts à utiliser dans l’algorithme de la distance d’édition de graphes est une étape importante. Il dépend du domaine d’application. Nous avons donc choisi les coûts suivants pour chaque type d’opération :
- les coûts de suppression et d’insertion d’un composant n doivent être > 0, nous avons choisi les valeurs : cnd(n) = cni(n) = 1 ;
- le coût de substitution d’un composant est : cns(n,v) = 2 si les composants n et v ont des étiquettes différentes, cns(n,v) = 0 si les étiquettes des composants n et v sont identiques. En effet, l’opération de substitution de deux composants ayant des étiquettes différentes correspond à effectuer une opération de suppression (du premier composant), suivie d’une opération d’insertion (du deuxième composant), d’où la valeur choisie de 2 ;
- les coûts de suppression et d’insertion de l’arc i sont : ced(i) = cei(i) = 1 ;
- les connexions d’un SE n’ont pas d’étiquettes. Pour le coût de substitution, nous avons utilisé le sens de la connexion de telle façon que : ces(i,j) = 2 si les directions des connexions i et j sont opposées, ces(i,j) = 0 si les directions des connexions i et j sont identiques.
Pour cette expérimentation, nous avons procédé à un classement manuel des différents schémas des apprenants pour l’exercice présenté précédemment. Les schémas les mieux simplifiés sont classés au premier rang représenté par « 1 », les non simplifiés sont classés les derniers, au rang « 10 » (leur fonction logique n’ayant pas été simplifiée). Les autres sont classés entre 1 et 10, suivant les simplifications appliquées par l’apprenant et les appréciations de l’enseignant. Les schémas « incorrects » n’ont pas été classifiés manuellement, seul l’attribut « Incorrect » leur a été affecté pour le moment.

Nous avons ensuite comparé l’évaluation de l’enseignant avec la mesure de similarité entre schémas électroniques. Pour cela, nous avons choisi un seul schéma de référence par sortie (celui dont l’enseignant estime qu’il doit être classé comme premier de la liste), et nous avons calculé la similarité entre les productions des apprenants par rapport à ce schéma de référence. Tous les circuits des apprenants ont été comparés à ce même circuit de référence, même ceux dont la table de vérité est considérée comme « incorrecte ».

Figure 9• Évaluation sommative manuelle et mesure de similarité
La figure 9 compare l’évaluation sommative manuelle et la similarité pour les SE corrects, toutes deux normalisées (en divisant toutes les valeurs par la valeur maximale, c’est-à-dire 10 pour l’évaluation sommative et 27 pour la similarité). La courbe bleue en traits pleins (avec des étoiles) représente l’évaluation de l’enseignant. Celle en pointillés rouges (avec des ronds) représente la similarité entre les SE des apprenants et le SE de référence. Nous remarquons que la dynamique de ces deux courbes est la même. Le calcul du coefficient de corrélation entre ces deux séries de données est de 0,94 (pour rappel, une valeur de 1 indique que les données sont linéairement corrélées, et 0 pas du tout). Notre mesure de similarité pourrait donc être utilisée pour aider à faire de l’évaluation sommative des SE corrects.
5. Utilisation d’un algorithme d’apprentissage pour une évaluation diagnostique
Avant de vérifier qu’il est possible de faire de l’évaluation diagnostique à l’aide d’un algorithme de classification, il faut définir ce qu’est l’évaluation diagnostique dans notre contexte.
5.1. Évaluation diagnostique d’un schéma électronique
Lorsqu’un enseignant évalue le SE produit par un apprenant, il mesure deux paramètres. Tout d’abord, il étudie la table de vérité du SE. Soit cette table de vérité est correcte, soit elle ne l’est pas. Lorsqu’elle ne l’est pas, trois cas de figure se présentent. Dans le premier cas, les erreurs sont dites « typiques », c’est-à-dire que ces erreurs, liées à l’exercice, sont régulièrement commises par les apprenants. Dans le deuxième cas, les erreurs de la table de vérité ne sont pas interprétables mais la topologie du SE l’est bien, et son étude montre qu’il y a quelques oublis (par exemple un lien entre deux composants a été oublié), ou inversions (l’étudiant a confondu les symboles représentant les portes and et or). Ces erreurs sont appelées « erreurs de construction ». Enfin dans le dernier cas, la table de vérité du SE et sa topologie ne sont pas interprétables par l’enseignant.
Ensuite, dans le cas où le SE de l’apprenant est interprétable (grâce à la table de vérité ou à la topologie du SE), l’enseignant peut évaluer le niveau de simplification de l’expression booléenne que l’apprenant a su mettre en œuvre. Le nombre de niveau de simplification d’une expression étant lié à sa complexité (et donc à l’exercice), cette évaluation peut être normalisée entre 0 et 1 (0 pour une expression sans aucune simplification et 1 pour une expression totalement simplifiée).
Formellement, faire l’évaluation diagnostique du SE (à une seule sortie) d’un apprenant pour un exercice donné, revient à définir la fonction suivante (où ErreursTypiques représente l’ensemble des erreurs typiques de l’exercice) :
![]()
Par exemple, dans le cas de l’exercice sur l’additionneur binaire, pour la sortie Si, il existe deux erreurs typiques (qui sont l’oubli de la retenue et le fait de ne pas savoir l’utiliser), et le nombre de simplifications est de trois. La figure 10(a) présente le SE d’un apprenant dont l’évaluation diagnostique est le tuple (correct, 1) alors que la figure 10(b) présente le SE d’un autre apprenant dont l’évaluation diagnostique est le tuple (ne_sait_pas_utiliser_retenue, 0).
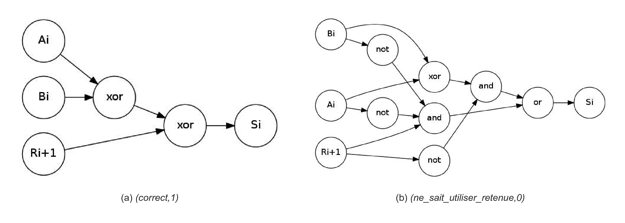
Figure 10• Deux évaluations diagnostiques
5.2. Algorithme de l’évaluation diagnostique des schémas électroniques
Nous avons vu dans la section 3.3 que l’algorithme du k-ppv est l’algorithme à utiliser dans le cadre d’une évaluation de productions d’apprenants. Il reste alors à définir quelle valeur de k choisir, et voir s’il est possible d’optimiser la phase de décision.
De manière générale, en apprentissage automatique et en particulier pour le k-ppv, la valeur à affecter à un paramètre est un problème difficile. Dans notre cas, le nombre d’exemples par classe sera assez restreint, le fait de prendre une valeur de k trop importante (supérieure au nombre d’éléments par classe) risque de remonter de l’incertitude. De plus, (Duda et al., 2001) indique que le 1-ppv fait partie des meilleurs classifieurs. Nous avons donc choisi de l’utiliser.
Il nous faut aussi optimiser la phase de décision. En effet, nous savons que le k - ppv n’est pas performant sur ce point, et qu’en plus le calcul de similarité entre deux SE est une opération coûteuse en temps et qui va être effectuée n fois (avec n le nombre d’éléments de la base d’apprentissage). Nous avons donc introduit des filtres dans la base d’apprentissage avant d’effectuer le calcul de mesure de similarité. Tout d’abord, un SE de l’apprenant n’est « comparé » à un autre schéma de référence de la base d’apprentissage que s’ils ont la même table de vérité. Si aucun SE de la base d’apprentissage ne possède la même table de vérité, c’est qu’il y a éventuellement une « erreur de construction » pour un schéma incorrect. Dans ce cas, nous comparons ce schéma à tous les autres schémas corrects de la base d’apprentissage, mais à condition que la différence des nombres de composants entre les deux schémas soit inférieure à un certain nombre de composants (pour notre expérimentation, nous avons choisi ce nombre égal à 3, car au delà de cette valeur, le temps de calcul de la mesure de similarité entre les deux schémas augmente rapidement). Dans tous les autres cas, un SE sera défini comme « non interprétable ». Ceci est formalisé par l’algorithme 2.

5.3. Validation à partir d’une base d’apprentissage construite manuellement
Dans un premier temps, nous avons construit notre base de données d’apprentissage de façon manuelle. Elle est constituée de deux catégories de données : les SE « corrects » et les SE « incorrects » issus de l’erreur typique « oubli de la retenue dans la sommation ». Chaque SE, de chaque catégorie, est aussi étiqueté par son degré de simplification (il y en a trois).
Le contenu de cette base pour les exemples « corrects » est le suivant :
- trois exemples simplifiés de manière optimale, étiquetés (correct, 1).
- trois exemples simplifiés de manière semi-optimale, étiquetés (correct, 0,5).
- un exemple sans simplification, étiqueté (correct, 0).
Pour les exemples « incorrects », la même organisation a été choisie, c’est-à-dire trois SE avec l’étiquette (oublie_retenue_dans_sommation, 1), trois autres SE avec l’étiquette (oublie_retenue_dans_sommation, 0,5) et un SE avec l’étiquette (oublie_retenue_dans _sommation, 0).
Le choix de « sept » exemples par catégorie n’est pas arbitraire. D’un côté, il fallait les créer manuellement et donc limiter leur nombre et d’un autre côté, ces exemples ont été choisis de telle façon que nous puissions avoir, sur une échelle de 1 à 10 correspondant au classement manuel de l’enseignant, des SE représentants certains niveaux de simplification.
En effet, sur les sept exemples des schémas corrects, il y a trois exemples qui représentent des SE classés « 1 » par rapport à l’échelle de classement de l’enseignant (simplification optimale), trois exemples qui représentent des SE classés « 5 » (simplification semi-optimale) et un seul exemple (en effet il n’existe qu’une et une seule expression logique sans aucunes simplifications d’une fonction logique) qui représente le classement « 10 » (aucune simplification). Les SE des apprenants seront donc comparés à ces sept exemples en fonction des simplifications qu’ils ont effectuées.
Le même raisonnement correspond aux exemples incorrects, sauf que dans ce cas, nous n’avons représenté qu’une seule erreur-type pour l’exercice.
5.3.1. Description de l’expérimentation
Dans cette deuxième expérimentation, les résultats que nous obtenons ne correspondent pas à un classement, mais à la mesure de similarité minimale par rapport à un SE de référence de la base d’apprentissage. Une partie des résultats (sortie Si) est présentée par la figure 11. En abscisse, il y a les SE des apprenants, en ordonnée la distance au SE sélectionné par le 1-ppv (l’étiquette de ce SE est indiquée au niveau du point). Les ronds bleus représentent les SE correctes et les triangles rouges les SE incorrectes.
Nous constatons que :
- les mesures de similarité obtenues ont diminué suite à l’augmentation du nombre de SE de référence dans la base d’apprentissage (le SE correct le plus éloigné est maintenant à une distance de 7 alors qu’il était à une distance de 27 dans l’expérience précédente). Nous avons pu identifier avec « exactitude » (mesure de similarité égale à zéro) plus de SE corrects (près des 2∕3 des schémas corrects) ;
- dans les autres cas (mesure de similarité différente de zéro), le SE sélectionné par l’algorithme du 1-ppvSE se trouve à une distance faible. Toutefois, puisque la mesure n’est pas égale à zéro, nous ne sommes pas sûrs que c’est la bonne évaluation que nous obtenons. La seule remarque que nous pouvons faire pour le moment, est que les résultats affichés ont permis de classer, à une mesure de similarité de 2, 1/6 des schémas corrects, et pour les schémas corrects restants, ils ont été classés à une mesure de similarité supérieure à 4 ;
- finalement, les mesures de similarité des schémas qui ont une table de vérité incorrecte ont diminué car le nombre de schémas de référence a augmenté.

Figure 11• Résultats du 1-ppv sur la sortie Si de l’additionneur
5.4. Validation à partir d’une base d’apprentissage construite automatiquement
Nous confirmons donc la nécessité d’augmenter le nombre d’exemples de la base d’apprentissage. Toutefois, il n’est pas raisonnable de les introduire de façon « manuelle ». Nous avons donc décidé de les produire de façon automatique. En effet, à partir d’une table de vérité et d’une liste d’erreurs pouvant se produire dans la même table (correspondant à des erreurs-types par exemple), il est possible de générer des SE « corrects » et « incorrects », correspondants à plusieurs niveaux de simplification.
5.4.1. Générateur (semi-)automatique de schémas électroniques
La difficulté pour la génération automatique de SE réside dans l’obtention de plusieurs niveaux de simplification à partir d’une même table de vérité. La solution que nous avons utilisée est inspirée de la méthode de Quine-McCluskey (Quine, 1952) et (McCluskey, 1956). Elle permet de produire automatiquement un ensemble de SE issus d’une même table de vérité. Seul le niveau de simplification de leur fonction logique de base est différent. Ce niveau varie entre le niveau « non simplifié » (niveau 0) et le niveau le « plus simplifié » (niveau n). Les niveaux intermédiaires correspondent à des simplifications intermédiaires de la fonction logique.
La figure 12 explique le fonctionnement du générateur de SE que nous avons développé. Il faut fournir en entrée une « table de vérité » d’un circuit logique et une liste « d’erreurs-type » correspondant à des erreurs classiques généralement commises pour ce circuit. À partir de la table de vérité, combinée éventuellement à une erreur-type (dans le cas de schémas corrects, aucune erreur n’est transmise au générateur), le générateur génère des « expressions booléennes étiquetées ». Chaque étiquette est composée du « statut » correct ou incorrect de la table de vérité, du type d’erreurs dans le cas des circuits incorrects, et du niveau de simplification de l’expression booléenne. Ensuite, l’ensemble des résultats obtenus est l’union de plusieurs sous-ensembles, regroupant chacun les expressions booléennes ayant les mêmes « étiquettes ». Finalement, les expressions booléennes étiquetées sont converties en SE étiquetés. L’ensemble obtenu représente la base d’apprentissage de notre algorithme de classification supervisée.

Figure 12• Principe de fonctionnement du générateur de SE
Le terme (semi-)automatique vient du fait, qu’en plus du générateur automatique décrit ci-dessus, nous rajoutons « manuellement » un autre niveau de simplification (n + 1). Ce niveau correspond à l’utilisation d’opérateurs logiques composés, tels que le xor ou le nxor.
5.4.2. Description et interprétation de l’expérimentation
Pour valider cette expérimentation, nous avons repris les mêmes productions des apprenants. Nous avons ensuite exécuté l’algorithme d’évaluation en utilisant :
- l’algorithme de classification 1-ppvSE, comme précédemment ;
- la mesure de similarité entre SE : dSE ;
- la nouvelle base d’apprentissage, plus complète, qui a été générée semi-automatiquement. Cette base contient des schémas corrects correspondants à plusieurs niveaux de simplification (26 schémas corrects). Pour les schémas incorrects, 8 types d’erreur ont été représentés dans la base d’apprentissage (chaque type correspond à une seule erreur sur une ligne de la table de vérité). Pour chaque type d’erreur, les schémas correspondants ont été générés sur plusieurs niveaux de simplification (soit au total, 66 schémas incorrects).
Les résultats de cette expérimentation représentent les mesures de similarité du schéma de l’apprenant par rapport à ceux de la base d’apprentissage ayant la même table de vérité. Un SE, dont la mesure de similarité est minimale par rapport à un SE de référence de niveau « n », appartient le plus probablement à cette catégorie de schémas.
En plus, nous avons considéré qu’un SE incorrect de l’apprenant et un SE correct de la base d’apprentissage sont « graphiquement proches » (donc, une possibilité d’erreur de construction), s’ils ont au maximum une seule porte logique à deux entrées qui les différencie. Ceci revient à ajouter, à l’un des deux schémas, un composant, plus trois connexions pour les rendre identiques, c’est-à-dire que la mesure de similarité entre les deux schémas est inférieure ou égale à 5 (= 2 pour la substitution ou insertion d’un composant + 3 pour la substitution ou l’insertion de 3 connexions).
Les résultats obtenus par cette expérimentation pour la sortie Si des 64 schémas des apprenants pour l’exercice de l’additionneur sont les suivants :
- 59 schémas ont été évalués « corrects » et identifiés de façon « exacte » dans la base d’apprentissage ;
- 1 schéma évalué « correct » et identifié de façon rapprochée (à une distance de 5 d’un circuit de référence de niveau 2) ;
- 4 schémas ont été évalués « incorrects » : 1 schéma a été identifié de façon exacte, un autre correspondait à une erreur de construction et les deux derniers n’ont pas pu être identifiés.
Ce qui nous donne un taux d’évaluation avec identification « exacte » dans la base d’apprentissage de 94%. Pour la sortie Ri du même exercice, le taux d’identification « exacte » est de 92%.
6. Conclusions et perspectives
6.1. Conclusion
Dans cet article, notre problématique était de concevoir un système d’aide à la correction de productions d’apprenants nécessitant un « savoir-faire », avec les deux contraintes suivantes :
- peu de connaissances doivent être explicitées au sein du système ;
- peu de connaissances doivent être explicitées au sein de chaque exercice.
Nous avons fait l’hypothèse que les techniques proposées en apprentissage automatique nous permettraient d’atteindre cet objectif. Pour valider cette hypothèse, nous avons adopté une démarche scientifique reposant sur des cycles « hypothèse-expérimentation-validation ». Chaque cycle était constitué des étapes opératoires suivantes :
- émettre une hypothèse ;
- développer les outils nécessaires pour sa vérification ;
- expérimenter avec des données du domaine et récupérer les résultats fournis ;
- vérifier et interpréter les résultats pour éventuellement valider l’hypothèse de départ.
Nous avons ainsi opéré trois cycles successifs. La validation de chaque cycle était nécessaire pour poser l’hypothèse suivante.
Le premier cycle correspondait à la validation d’une mesure de similarité entre SE. Cette mesure a été confrontée à des données réelles du domaine pour une première expérimentation. Durant cette phase, nous avons comparé l’évaluation sommative de l’enseignant avec la mesure de similarité entre schémas électroniques. Les résultats obtenus par la mesure de similarité respectent bien l’évaluation de l’enseignant.
Le deuxième cycle avait pour objectif de faire une évaluation diagnostique à l’aide d’un algorithme de classification. Pour cela nous avons choisi l’algorithme de classification des k plus proches voisins (en choisissant le cas le plus simple où k = 1) avec une base d’apprentissage construite manuellement, composée de SE corrects et incorrects correspondant à plusieurs niveaux de simplification. Nous avons ainsi pu identifier de façon très proche plus des deux tiers des productions « correctes » des apprenants.
Dans le troisième cycle, nous avons voulu affiner cette évaluation diagnostique et l’étendre à d’autres exercices. Nous avons ainsi développé un « générateur de SE ». Ce générateur permet de produire automatiquement, à partir d’une table de vérité et d’erreurs types, des schémas « corrects » et « incorrects ». Dans tous les cas, les schémas produits correspondent à plusieurs niveaux de simplification. Nous avons repris les productions des apprenants pour une nouvelle expérimentation, soit 128 schémas électroniques pour l’exercice de l’additionneur binaire, regroupant les 64 schémas pour la sortie Si et les 64 schémas pour la sortie Ri. Les résultats obtenus ont confirmé une nette augmentation dans le taux d’identification (95% pour les circuits corrects au lieu de 66% pour l’expérimentation précédente).
Nous avons confronté notre prototype à deux autres exercices, dont les résultats n’ont pas été présentés dans cet article. Le soustracteur binaire, regroupant 124 schémas électroniques pour les deux sorties du circuit correspondant, et le complément à 2, regroupant 64 schémas électroniques pour les 4 sorties du circuit correspondant. Pour l’ensemble des schémas électroniques des trois exercices, le taux d’identification des circuits corrects était d’environ 91%. Pour les circuits incorrects, nous sommes arrivés à poser des hypothèses sur l’origine des erreurs dans à peu près 56% des cas.
Enfin, pour les SE qui n’ont pas été identifiés ou qui ont été rejetés par le moteur d’évaluation, l’enseignant a toujours la possibilité de les étiqueter « manuellement » et de les insérer dans la base d’apprentissage pour des évaluations ultérieures. C’est une manière d’enrichir progressivement la base d’apprentissage avec des exemples « intéressants » et qui n’ont pas pu être générés automatiquement.
Au vu de ces résultats, notre prototype est donc une aide significative à la correction de SE des apprenants. Mais avons-nous pour autant satisfait les deux dernières contraintes que l’on s’était données ?
Pour ce qui concerne les connaissances du domaine explicitées au sein du système d’évaluation, nous pensons que l’objectif est en partie atteint. En effet, le système repose sur l’utilisation d’un algorithme de classification, d’une mesure de similarité et d’un générateur d’exemples. L’algorithme de classification est indépendant du domaine. La mesure de similarité utilise un algorithme d’édition de graphes où seules les heuristiques sont dépendantes du domaine. Enfin, seul le générateur d’exemples est totalement lié au domaine.
Au niveau des connaissances explicitées pour chaque exercice, l’enseignant doit fournir une table de vérité et un ensemble d’erreurs typiques (une erreur étant la modification d’une ou plusieurs lignes de cette table de vérité). Nous pensons donc que cette contrainte est en grande partie respectée.
6.2. Perspectives
Aujourd’hui, l’outil que nous avons proposé pour l’évaluation des SE est un « prototype ». Il reste encore des développements et des améliorations à effectuer pour avoir un produit utilisable et diffusable. Pour les évolutions futures de nos travaux, nous distinguons deux catégories de perspectives : des considérations techniques et des perspectives de recherche.
Pour les considérations techniques, il faut essentiellement continuer le développement pour passer du prototype à une application utilisable et qui pourra être intégrée dans la plate-forme TEB. Le re-développement des algorithmes, qui sont écrits pour l’instant en langage Python, nécessitera sans doute des adaptations et réajustements pour leur exportation au langage de programmation de la plate-forme TEB (Technologie JEE). Nous préconisons aussi que les développements du composant d’évaluation respectent le standard SCORM, afin de permettre à l’application d’être lue par un « player » SCORM, ce que nous retrouvons dans la plus part des plates-formes actuelles (comme par exemple, Moodle, Claroline, WebCT, etc.).
Une autre considération technique est l’amélioration des performances et des fonctionnalités de notre outil. Par exemple il faudrait que le générateur automatique de SE puisse prendre en compte le niveau de simplification (n + 1). Ce niveau utilise les opérateurs logiques composés, tels que le xor ou le nxor. Ce niveau de simplification pourra être développé à partir des explications qui sont proposées dans (Turton, 1996).
Pour les perspectives de recherche, il faudrait mener une réflexion sur l’utilisation d’autres algorithmes de classification, plus performants en temps de calcul, mais qui permettent aussi d’effectuer « un rejet par distance ».
De plus, nous pensons que notre méthode pourrait être généralisée à d’autres domaines. Cette généralisation pourrait se faire moyennant quelques développements supplémentaires. Par exemple, nous travaillons actuellement sur l’évaluation du savoir-faire des apprenants dans le domaine de l’algorithmique, les algorithmes produits par les apprenants pouvant être représentés entre autres par des graphes.
Un autre exemple est celui des résultats de travaux de thèse de L. Auxepaules (Auxepaules, 2009). Il s’est intéressé à l’analyse et au diagnostic des réponses de l’apprenant dans des activités de modélisation, plus particulièrement, la construction de diagrammes UML. L’outil de diagnostic qui est proposé se base sur la comparaison et l’appariement entre le diagramme de l’apprenant et un seul diagramme de référence fourni par l’enseignant. Bien que l’objectif pédagogique ne soit pas le même, nous pensons que notre démarche pourrait être appliquée au domaine de la modélisation UML. En effet tout diagramme UML peut être représenté par des graphes ayant 3 types de nœuds : classe, attribut et méthode, et 4 types de liens : association, agrégation, composition et héritage. L’algorithme sur la distance d’édition entre graphes (GED) pourrait ainsi être adapté à ce cas afin de calculer une mesure de similarité entre diagrammes UML. La difficulté ne résiderait alors plus que dans la génération automatique de diagrammes à partir d’un modèle de référence de l’enseignant. Nous pouvons toutefois émettre l’hypothèse que notre méthode basée sur l’utilisation d’erreurs types (confusion entre composition et attribut, confusion entre composition et agrégation, etc.), pourrait dans ce cadre générer plusieurs diagrammes UML à partir d’un exemple de l’enseignant.
Finalement, une autre perspective serait d’étendre « l’aide à la correction » proposée par notre méthode à « l’aide à l’auto-correction ». En effet, actuellement l’outil propose une aide à la correction à l’enseignant pour l’évaluation diagnostique des productions des apprenants. Nous réfléchissons sur l’évolution de cet outil pour qu’il puisse proposer cette aide directement à l’apprenant dans un processus d’auto-formation.
BIBLIOGRAPHIE
AUXEPAULES L. (2009). Analyse des diagrammes de l’apprenant dans un EIAH de la modélisation orientée objet. PhD thesis, Université du Maine.
BUNKE H. et ALLERMAN G.(2001) Inexact graph matching for structural pattern recognition. In Pattern Recongnition Letters, volume 1, pages 245–253. Elsevier Science Publisher.
BOOLE G.(1854) An Investigation into the Laws of Though on Which Are Founded the Mathematical Theories of Logic and Probabilities. Dover Publications, New York.
BUNKE H. (1997). On a relation between graph edit distance and maximum common subgraph. In Pattern Recognition Letters, vol. 18, p. 689–694. Elsevier.
CANU S. (2007).Machines à noyaux pour l’apprentissage statistique. In Technique de l’ingénieur, vol. TE5255.
DARCHE P. (2002). Architectures des ordinateurs : Fonctions booléennes, logiques combinatoire et séquentielle, vol. 2. Vuibert Informatique.
DELORME F.(2005) Evaluation et modélisations automatiques des connaissances des apprenants à l’aide de cartes conceptuelles. PhD thesis, INSA de Rouen.
DUDA R., HART P., STORK D. (2001) Pattern Classification. Wiley Interscience.
KARNAUGH M. (1953) The map method for synthesis of combinational logic circuits. In Trans. AIEE, vol. 72, p. 593–599.
KOHONEN T. (1982). Self-organized formation of topologically correct feature maps. Biological Cybernetics, 43(1) p.59–69.
MESSMER B.T. et BUNKE H. (1998). A new algorithm for error-tolerant subgraph isomorphism detection. In IEEE Transaction on Pattern Analysis and Machine Intelligence, vol. 20, p. 493–504.
McCLUSKEY E.J. (1956). Minimization of boolean functions. In Bell System Tech. J., vol. 35, p. 1417–44.
MITCHELl T.M. (1997) Machine Learning. McGraw-Hill Science.
NILSSON N.J. (1980) Principles of Artificial Intelligence. Tioga Publishing.
NKETSA A. (1998) Circuits logiques programmables. Ellipses.
NEUHAUS M., RIESEN K., BUNKE H. (2006). Fast suboptimal algorithms for the computation of graph edit distance. In 11th International Workshop on Structural and Syntactic Pattern Recognition, p. 163–172. Springer.
QUINE W.V. (1952) The problem of simplifying truth functions. In Amer. Math. Monthly, vol. 59, p. 521–531.
RIESEN K. et BUNKE H. (2008). Approximate graph edit distance computation by means of bipartite graph matching. Elsevier, 27(7) p. 950–959.
SCHöLKOPF B., WILLIAMSON R.C., SMOLA A.J., SHAWE-TAYLOR J., PLATT J. (2000). Support vector method for novelty detection. Advances in neural information processing systems, vol. 12 p.582–588,.
TURTON B.C. H. (1996) Extending quine-mccluskey for exclusive-or logic synthesis. In IEEE Transaction on Education, vol. 39, p. 81–85.
VAPNIK V.N. (1998) Statistical Learning Theory. Wiley.
ZANELLA P. et LIGIER Y. (1998) Architecture et Technologie des ordinateurs. Dunod, 3˚edition.
 À
propos des auteurs
À
propos des auteurs
Référence de l'article :
Mariam Tanana, Nicolas Delestre, Revue STICEF, Volume 17, 2010, ISSN : 1764-7223, mis en ligne le 18/03/2011, http://sticef.org

© Revue Sciences et Techniques de l'Information et de la Communication pour l'Éducation et la Formation, 2010