Sommaire

Rechercher

• auteur
• année
• titre
• résumé
• abstract
• rubrique

Contact : infos@sticef.org

Description et exploitations des traces du logiciel d’algèbre Aplusix

Hamid CHAACHOUA, Marie-Caroline CROSET, Denis BOUHINEAU, Marilena BITTAR, Jean-François NICAUD LIG, Grenoble

RÉSUMÉ : Cet article porte sur l’emploi de traces dans un contexte éducatif et sur leur utilisation dans un EIAH. La première partie présente le logiciel Aplusix, un micromonde pour l'apprentissage de l'algèbre qui permet l’enregistrement de productions d’élèves, comme celles obtenues dans l'environnement classique papier, mais comportant de plus d'autres informations, comme le temps, les hésitations, les corrections. Ce recueil produit une trace brute qui représente une modélisation comportementale des élèves dont les utilisations sont immédiates (visualisation, statistiques). La deuxième partie porte sur des traitements et diagnostics locaux effectués sur ces traces dans l'environnement informatique Anaïs. Ce logiciel procède à une restriction, un découpage et une interprétation des traces brutes et mène à la production d’une trace enrichie contenant des règles algébriques expliquant les transformations des élèves et identifiant le contexte où elles apparaissent. La troisième partie présente une modélisation globale des connaissances des élèves, avec une étude de cas sur la résolution des équations de degré 1. La modélisation des élèves s'est appuyée sur la confrontation des analyses manuelles et automatiques d'expérimentions ayant eu lieu dans des établissements scolaires de différents pays. MOTS CLÉS : Algèbre, connaissance, diagnostic, micromonde, modélisation, trace.

ABSTRACT : This article is about the place of traces in education and legitimates their use in TEL. The first part presents the Aplusix learning environment which allows students to freely make calculation steps, as they do in the paper environment, and which records all the students’ actions in logs. From these logs, visualisation and statistics are built. The second part is about local diagnostic of the learner and production of enriched trace: a student’s transformation is diagnosed with a sequence of rewriting rules. A library of correct and incorrect rules has been built for that purpose. The third part is about global model of the learner in the field of the movement concept in equations and inequations. KEYWORDS : Algebra, diagnosis, knowledge, microworld, trace, user-modelling

1. Introduction

2. Recueil, représentation et visualisation des traces

3. Définition d’un diagnostic local pour l’obtention d’une trace enrichie

4. Modélisation globale des connaissances de l’élève

5. Conclusion et perspectives

BIBLIOGRAPHIE

ANNEXES

1. Introduction

Un des objets d'étude important en didactique est la modélisation des connaissances des élèves. Dans ce domaine, le travail du chercheur commence par le recueil de données expérimentales issues d’un milieu écologique d’apprentissage, ayant la forme de productions écrites ou orales d’élèves, données que nous appelons traces ou traces brutes. À partir de ces traces, le chercheur poursuit habituellement son travail à la main par un découpage et une réorganisation raisonnée de ces traces. Au final, après une opération experte de modélisation, le chercheur aboutit à un modèle des connaissances des élèves en général, et de chaque élève en particulier. Lorsqu’il est appliqué à un nombre assez important d’élèves, ce processus est long et fastidieux.

L’automatisation partielle des trois phases de ce processus peut être entreprise en considérant les environnements informatiques pour l’apprentissage humain disponibles aujourd’hui, pourvu que :

- le recueil des productions d’élèves puisse se faire automatiquement. Ce qui est le cas lorsque les séquences d’apprentissage se déroulent sur un ordinateur et que les logiciels utilisés disposent de fonctionnalités élémentaires d’enregistrement de journaux d’activités (fichiers « log ») ;

- le découpage et la réorganisation des traces brutes obtenues à l’étape précédente puissent se faire automatiquement. C’est le cas lorsque qu’un algorithme de diagnostic local est disponible (ce qui est parfois le cas), le résultat, réorganisé linéairement en fonction du temps, peut être vu comme une trace enrichie de l’activité de l’élève ;

- la dernière étape du processus, la modélisation des connaissances des élèves, soit computationnelle et effectivement mise en œuvre dans un environnement informatique. Cette condition est plus rarement réalisée.

Lorsqu’elle est effective, cette automatisation permet au chercheur d'accéder à un traitement de données importantes, pour des études comparatives entre plusieurs classes d'un pays ou de plusieurs pays. Un autre intérêt de la mécanisation des diagnostics de connaissances des élèves est de fournir aux enseignants des informations personnalisées pour chaque élève. Enfin, le diagnostic automatique peut être utilisé pour aider les tuteurs artificiels dans leurs prises de décisions didactiques (Tahri, 1993), (Chaachoua & Lima, 2003).

Le passage du travail manuel et expert du didacticien au traitement automatisé n’a malheureusement rien d’évident et d’immédiat. Ce passage soulève des questions difficiles, en particulier concernant la transposition de la modélisation didactique à une modélisation respectant les contraintes de l’informatique.

L'objet de notre recherche porte sur le diagnostic automatique des connaissances des élèves en algèbre, effectué à partir des traces recueillies avec le logiciel Aplusix. Pour modéliser les connaissances de l’élève, nous avons choisi de nous référer à la théorie des champs conceptuels de (Vergnaud, 1991). Cette théorie postule que les conduites des élèves (hésitations, erreurs, décisions, etc.), dans des situations de résolution de problèmes, sont structurées par des schèmes. L'auteur définit le « schème » par L'organisation invariante de la conduite pour une classe de situations donnée. C'est dans les schèmes qu'il faut rechercher les connaissances-en-acte du sujet, c'est-à-dire les éléments cognitifs qui permettent à l'action du sujet d'être opératoire (ibid, p.136). Un schème repose sur :

- un ensemble d'invariants opératoires (théorèmes-en-acte et concepts-en-acte),

- des anticipations du but à atteindre,

- des règles d'actions qui permettent de générer les actions du sujet,

- des inférences ou des raisonnements qui permettent de calculer les règles d'actions et de mettre en œuvre le schème dans chaque situation particulière.

Un théorème-en-acte est un invariant de type proposition. Il est tenu pour correct ou incorrect, selon que son application est mathématiquement valide ou non. Les concepts se développent dans l’action et sous-tendent les formes d’organisation de l’activité que sont les schèmes. Il n’y a pas d’action possible sans propositions tenues pour vraies sur le réel. Ce sont justement ces propositions tenues pour vraies que j’appelle théorèmes-en-acte, y compris pour d’autres domaines d’activité que les mathématiques. Leur portée est souvent locale (elle l'est toujours dans la phase d'émergence); ils peuvent rester implicites; ils peuvent même être faux (Vergnaud, 2001).

Par exemple¹, un schème de résolution des équations de degré 1 de la forme ax+b=c repose sur des théorèmes-en-acte comme « on conserve l'égalité en soustrayant b des deux côtés » et des règles d'actions comme « si a+b=c alors a+b-b=c-b ».

Dans notre recherche, nous voulons déterminer automatiquement les règles d'actions et les théorèmes-en-actes relatifs à différentes activités algébriques transformationnelles, au sens de Kieran (Kieran, 2001)². Nous les classons en cinq genres de tâches : factorisation, développement, réduction, calcul et mouvement (dans une équation ou une inéquation).

Notre méthodologie de travail se décompose en quatre phases, automatisées pour ce qui est des trois dernières. Chaque phase est décrite dans l’une des sections de cet article :

- Construction des expérimentations (section 2).

- Recueils de traces par le logiciel Aplusix (section 1).

- Interprétation manuelle et automatique des transformations d’expressions algébriques par des applications de règles algébriques (section 2).

- Regroupement des règles de la phase précédente sous forme de règles d'action et de théorèmes-en-acte (section 3).

2. Recueil, représentation et visualisation des traces

2.1. Aplusix : l’environnement de recueil des données et contextes d’utilisations

L’environnement Aplusix (Nicaud et al., 2004) est un EIAH stable, mature et distribué dans plusieurs pays, pour pratiquer l’algèbre élémentaire, les transformations d’expressions algébriques, les résolutions d’équations, d’inéquations et de systèmes d’équations, au lycée et au collège. En dehors des éléments qui font explicitement usage des traces et qui seront décrits amplement dans cet article, il est composé, principalement :

- d’un micromonde d’édition des expressions algébriques, éditeur riche et souple, offrant diverses rétroactions syntaxiques et sémantiques,

- d’un module de génération automatique d’exercices comportant plusieurs centaines de patrons d’exercices,

- de modules pour l’enseignant (éditeur d’exercices, administration des comptes).

S’appuyant sur la trace des activités des élèves enregistrée en permanence, automatiquement, au cours de leur travail, l’environnement disponible en lycée et au collège comporte, de plus :

- un magnétoscope pour rejouer le travail d’un élève,

- un module de statistiques pour visualiser diverses informations globales (nombres d’exercices effectués, réussis, etc.), en cours de séance ou en différé, pour un élève ou un groupe d’élèves.

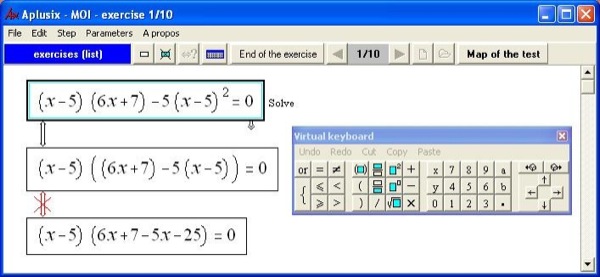
L’objectif de l’élève dans Aplusix consiste à résoudre, comme sur le papier, des problèmes d’algèbre en produisant, ligne de calcul après ligne de calcul, les différents pas de calcul de son raisonnement algébrique. Le cadre mathématique offert pour ce travail est la résolution par équivalence : l’élève doit, à chaque étape, donner une expression algébrique équivalente à l’expression précédente ; il a toute liberté, comme sur le papier, pour le choix de l’expression algébrique de l’étape courante et de la forme de son raisonnement (linéaire ou avec des retours en arrière). Cette grande liberté autorise des raisonnements n’aboutissant pas, progressant lentement vers une solution, ou s’en éloignant, et même l’introduction d’expressions algébriques non équivalentes à l’expression initiale, mal formée, ou en cours de définition. En général, les activités se déroulent en mode entraînement, des rétroactions sont fournies, en particulier deux rétroactions fondamentales. Tout d’abord, l’équivalence algébrique entre étapes est calculée en permanence et affichée de manière non intrusive. Ensuite, quand l’élève décide que l’exercice est terminé, une vérification syntaxique et didactique de la forme de l’expression solution de l’élève est effectuée et les résultats de cette analyse sont affichés. Il existe aussi un mode test où ces rétroactions sont absentes. Ce mode permet en particulier aux didacticiens d’effectuer des études de comportements d’élèves, sans les étayages fournis par le logiciel.

Au cours de la conception d’Aplusix, nous nous sommes efforcés de proposer une représentation des expressions algébriques utilisées à l’écran aussi fidèle que possible de la représentation usuelle de ces expressions, telle que chacun peut la donner sur le papier ou au tableau, cf. figure 1. Une part importante de notre travail initial a donc été consacrée à la définition de cette représentation, mais un temps plus important encore a été nécessaire à la spécification de la manière dont l’édition de ces expressions pouvait se réaliser, afin qu’elle soit la plus naturelle possible, tout en restant au maximum mathématique.

Figure 1 : Aplusix

Diverses utilisations et expérimentations d’Aplusix ont pu avoir lieu depuis les premières versions utilisables de l’environnement (Nicaud et al., 2002).

En faisant varier la durée :

- expérimentations courtes (moins de 4 heures, réparties en deux ou trois séances) en France et au Brésil,

- expérimentations sur 3 mois au Brésil ou encore

- expérimentations tout au long de l’année en France.

En faisant varier le nombre de participants :

- expérimentations sur un nombre conséquent d’élèves (plusieurs centaines en France, environ deux mille au Brésil) pour des recueils massifs de données, ou

- utilisation ponctuelle à l’hôpital en France.

En faisant varier les modalités du travail devant l’ordinateur :

- expérimentation pour un travail de groupe, collaboratif face à l’ordinateur en Inde ou

- expérimentations individuelles (1 élève par poste), en France.

En faisant varier le cadre pédagogique :

- expérimentation dans le cours normal de l’enseignement ou

- expérimentation lors d’utilisations exceptionnelles.

Enfin, en faisant varier l’objectif :

- expérimentation pour recueillir des comportements d’élèves,

• pour des analyses didactiques pointues ou

• des analyses en psychologie cognitive (France),

• ou encore, en vue d’évaluer les compétences des élèves (Brésil),

- expérimentation pour observer les usages

• concernant l’entraînement sur des techniques connues (France),

• concernant l’exploration de questions ouvertes (Italie),

• concernant l’apprentissage dans un cours ordinaire (Brésil),

• concernant la remédiation face à des difficultés repérées (France et Italie),

- expérimentation pour évaluer l’apprentissage (Brésil).

Les contextes, les langues, les sujets abordés, les niveaux, les modalités d’utilisation, les objectifs ont été variés. Cependant, en général, nous pouvons observer les constantes suivantes, dont certaines étaient induites par les fonctionnalités du logiciel :

- l’utilisation s’est déroulée en milieu écologique (quasiment pas d’utilisation en laboratoire),

• en salle du lycée ou du collège équipée en ordinateurs (souvent la salle dite « salle d’info »),

• en présence de l’enseignant (son rôle variant selon les expérimentations),

• en classe entière, en demi-classe ou en groupe de soutien (quasiment pas d’utilisation d’un individu isolé),

• sur une partie du curriculum (variant selon le pays et l’âge, mais restant dans le domaine de l’algèbre élémentaire),

- les outils fournis avec l’environnement de base reposant sur les traces (magnétoscope, statistiques) sont souvent ignorés, ou seulement utilisés après la séquence, principalement par les chercheurs (en laboratoire, en vue d’études spécifiques, avec les outils spécifiques de la recherche de diagnostic ou de modélisation des élèves),

- il n’y a pas eu d’outils de communication, de type forum, news, ou de discussions type irc, webchat, mis à disposition,

- la plupart du temps, il n’y a pas eu d’expérimentateur extérieur pour observer et retracer le déroulement de l’activité,

- et quasiment aucun enregistrement vidéo ou sonore n’a été effectué.

Les différences principales étaient :

- absence d’objectifs pédagogiques communs,

- absence de méthodologie d’enseignement partagée,

- absence de culture commune,

- absence de type d’exercice ou de niveau d’étude unique,

- absence de paramètres types de configuration de l’environnement.

Sur la période 2002-2006, pour une part répertoriée des expérimentations qui se sont déroulées avec Aplusix, nous comptons plus de 2 000 élèves enregistrés, 15 000 heures de protocoles, 80 000 exercices résolus, et plus de 4 000 000 actions observées. Le format de stockage des traces brutes (cf. section 1.3.1) ayant peu évolué, la masse de données ainsi obtenue peut être exploitée avec les mêmes outils, servir de données de référence, être échangée, etc. Il peut s’avérer que le plus difficile ne soit pas de s’adapter aux variations des formats des traces mais d’arriver à réunir l’ensemble des protocoles de provenances diverses et de savoir si l’on peut les amalgamer dans un tout bigarré : les objectifs et les contextes d’utilisations n’étant pas toujours les mêmes.

2.2. Traces brutes et traces enrichies

2.2.1. Nature des traces brutes

Dans l’EIAH Aplusix, la trace brute est obtenue par enregistrement des événements logiciels provoqués par un élève dans son travail de résolution de problèmes ou d’exploration d’expressions dans le micromonde d’édition d’expressions algébriques : les événements systèmes (frappes claviers, clics souris) induisent des appels de menus et de commandes, des éditions du document courant, éventuellement ces dernières provoquent l’envoi de messages d’erreurs, la plupart modifiant l’état du document (i.e., de l’expression algébrique en cours d’édition). L’ensemble de ces événements logiciels, modifiant ou non l’état de l’EIAH, est conservé sous la forme d’une liste de n-uplets. Chaque n-uplet comporte principalement un marqueur temporel, une information symbolique sur l’action réalisée et l’état du document (expression algébrique de l’étape courante) accompagné du contexte d’édition obtenu à la fin de son exécution (position du curseur d’édition, présence de sélection). C’est une forme classique Temps-Transition-État de relevé de traces des systèmes de collecte de traces.

La trace brute ainsi obtenue est très riche. Elle comporte toutes les expressions algébriques produites par l’élève (l’un des items du n-uplet précédent) et le film des actions réalisées par cet élève (suite de ces n-uplets). En particulier, les didacticiens sont forts intéressés par l’accès qu’ils obtiennent ainsi à la zone privée d’édition (le brouillon) de l’élève. En effet, la trace comporte les essais fructueux, ceux qui apparaîtront dans la solution finale, et les essais infructueux, qui seront effacés après avoir été visualisés, explorés puis abandonnés.

Cependant, cette trace comporte aussi beaucoup d’informations qui ne ressortent pas du travail mathématique, du travail arithmétique, ou algébrique, ou du travail au niveau stratégique de résolution d’un problème algébrique. En effet, elle cherche à conserver fidèlement l’activité de l’élève et comporte aussi, en conséquence, toutes les informations liées à l’activité primaire d’édition de l’élève. Entre autres, parmi ces informations d’édition, certaines sont sans effet sur l’état, restreint aux aspects mathématiques, de l’environnement (par exemple : modification de la position de la souris ou d’une sélection). En effet, nombre d’états de l’EIAH sont des états intermédiaires d’édition. Il s’agit souvent d’états comportant des expressions algébriques mal formées, ce qu’il est facile de repérer. Mais ce n’est pas tout. Il y a aussi des états comportant des expressions bien formées mais qui sont sous-expressions ou sur-expressions de la forme finale recherchée, ou mélange entre plusieurs formes possibles, ce qu’il est plus difficile de diagnostiquer. Malheureusement, la proportion entre états cohérents et significatifs d’un point de vue mathématique, et états incohérents ou non significatifs est faible. Nous y reviendrons plus tard.

Enfin, aussi riche que cette trace brute puisse sembler, elle ne vise pas à être exhaustive et ne l’est pas. Certaines informations sont délibérément perdues. Pour exemple, les mouvements de souris, lorsqu’ils ne sont pas associés à des clics, ne sont pas enregistrés. Le fait que l’appel d’un menu soit effectué avec la souris, ou directement au clavier, n’est pas conservé ; cet appel est représenté de la même manière dans les deux cas. D’autres exemples pourraient être donnés. Aussi paradoxal que cela puisse paraître, ces traces ont pour objectif d’être petites. Ainsi, pour optimiser la taille de ces traces, certaines informations, (re)calculables si nécessaire en fonction des informations enregistrées, ne sont pas inscrites dans les traces, par exemple les scores des exercices ou les textes des messages d’erreurs, d’aides ou d’explication et (dans une version précédente) la valeur de certains indicateurs visuels stratégiques d’avancement.

2.2.2. Travail de segmentation des traces brutes

Pour la plupart des traitements « intelligents » qui suivent, un premier travail de segmentation de la trace est opéré pour ne conserver que des éléments significatifs de la trace brute. Des critères drastiques sont utilisés, permettant de filtrer l’ensemble des états intermédiaires d’édition, quitte à supprimer aussi quelques éléments significatifs. Ces critères reposent sur certains événements logiciels considérés comme des indicateurs de validation par l’élève d’un état intermédiaire, cohérent de son travail : introduction, ou suppression, d’une étape algébrique dans le raisonnement de l’élève (équivalent de l’écriture d’une nouvelle ligne de calcul), demande de validation du travail, passage à l’exercice suivant.

En suivant les modèles d’analyses de la motivation et de la concentration des élèves (de Vicente & Pain, 1998), d’autres critères plus lâches auraient été possibles, en particulier reposant sur une analyse de l’aspect temporel de l’activité de l’élève faite conjointement avec une analyse de l’état de l’expression courante et, modulo l’adjonction d’un dispositif adéquat, d’une analyse des expressions faciales de l’élève. Ainsi, certains états auraient pu être analysés comme validés par l’élève, parce qu’ils correspondent à des expressions bien formées et des moments d’inactivité de l’élève (moments de réflexion pour anticiper la suite, ou moments de contrôle de l’expression obtenue) et conservés pour la suite. Ils n’ont pas été retenus, la segmentation grossière définie précédemment fournissant des traces déjà suffisamment riches et possédant une garantie forte de ne pas comporter d’informations non pertinentes, même si elles peuvent masquer certaines activités mentales d’anticipation et de contrôle.

À l’issue du travail de segmentation des traces brutes, les expressions algébriques significatives de l’élève obtenues sont associées par deux pour former des pas de calcul : à chaque expression significative est associée l’expression significative qui lui précède (dans le raisonnement algébrique de l’élève). Un pas de calcul d’élève comporte donc une étape initiale et une étape finale. Le mode d’édition libre permis par Aplusix ne permet pas de définir objectivement quelle opération (au sens large) a été utilisée par l’élève pour passer de l’une à l’autre. C’est d’autant plus vrai quand l’élève a fait des erreurs en appliquant une transformation algébrique correcte, ou s’il a appliquée une transformation algébrique incorrecte ; en faisant l’hypothèse qu’il a travaillé ainsi. La recherche d’une telle opération ou transformation est abordée en section 2.

Ce travail de segmentation s’effectue en vue des traitements automatiques complexes ultérieurs : analyses statistiques, diagnostic local du travail des élèves ou élaboration d’un modèle de l’élève. La visualisation au magnétoscope par les didacticiens des travaux d’un élève est exempte de ces segmentations. Les analyses statistiques reposent sur un filtrage plus fort ne conservant que l’état final du travail de l’élève.

2.2.3. Nature des traces enrichies

À partir de la segmentation précédente, une trace dérivée, importante dans notre système, est obtenue que nous appelons la trace enrichie ou trace complétée. Elle comporte, à la base, les pas de calcul d’élèves issus de la segmentation. Elle est enrichie d’un diagnostic constitué d’une proposition de règles de transformation expliquant le passage de l’expression initiale du pas de calcul à l’expression finale du même pas. Un algorithme utilisant une bibliothèque de règles correctes et incorrectes, mettant en œuvre une recherche heuristique, est utilisé pour effectuer ce diagnostic.

La mise au point de ce diagnostic et les résultats obtenus par ce diagnostic constitue la seconde partie de cet article.

2.3. Représentation, stockage

2.3.1. Représentation des traces sous forme de fichiers textes

En cours d’utilisation de l’EIAH par une classe, les traces brutes de chaque élève sont enregistrées localement sur l’ordinateur de l’élève (ou sur le serveur de l’établissement dans un répertoire attribué à l’élève, en cas d’utilisation en réseau, type réseau Windows©). L’enregistrement s’effectue au fur et à mesure de l’activité (à la fin de chaque exercice), sans gène pour l’utilisateur, sans demande expresse de celui-ci. Conçues pour être concises, les traces ont une taille qui varie linéairement en fonction du temps, une activité d’une heure pouvant représenter 50 ko. L’enregistrement de ces traces ne génère qu’une utilisation faible de l’ordinateur (ou un petit flux réseaux) lors des changements d’exercices.

Les fichiers d’enregistrement des traces sont des fichiers textes standard au format csv. Aussi, ils sont lisibles par l’homme. L’emploi des délimiteurs « ; » dans la structure de ces fichiers et des sauts de ligne fait qu’ils sont également manipulables facilement avec un tableur. L’objectif poursuivi, ici, est que ces traces soient facilement disponibles et exploitables par des non-informaticiens (didacticiens et psychologues). L’emploi de ces structures standard permet aussi des utilisations aisées par les informaticiens. En outre, ces fichiers peuvent être organisés en utilisant une arborescence normale de répertoires Windows© et les logiciels de diagnostics automatiques développés par nous sont adaptés en conséquence.

Au niveau de l’organisation interne, les fichiers peuvent comporter plusieurs sessions d’utilisation d’Aplusix. Chaque session commence par un entête contenant le contexte d’utilisation de l’EIAH :

- informations sur l’élève,

- informations sur les paramètres,

- options utilisées.

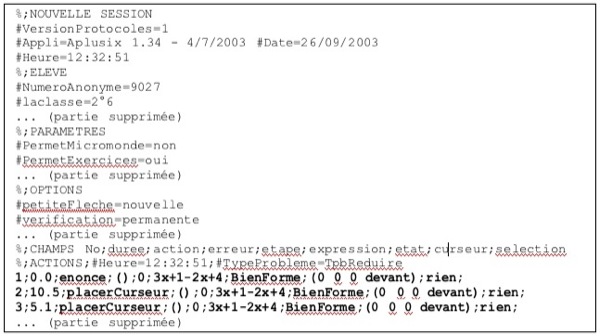
Le fichier comporte ensuite l’ensemble des actions enregistrées. Cette liste commence par :

- une ligne exprimant les noms des différents champs informés pour chaque action (ici,

« No;duree;action;erreur;etape;expression;etat;curseur;selection » exemple figure 2, un numéro d’ordre dans la trace (1, 2, 3, ...), la durée en seconde depuis la dernière action (0, 10.5, 5.1, ...), l’action ou transition observée (énoncé, placerCurseur, placerCurseur, ...), l’état et l’expression obtenue (3x+1-2x+4), s’il y a eu une erreur, le contexte pour le curseur et la sélection) et se poursuit avec

- chaque action enregistrée selon ce format.

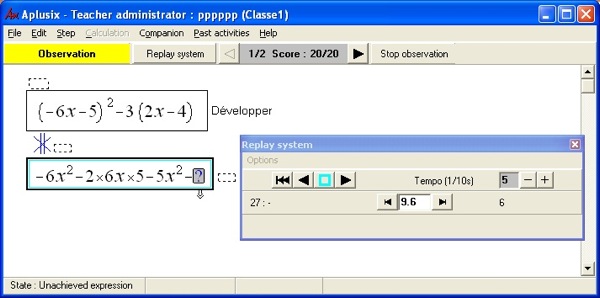
Figure 2 : Exemple de fichier de traces brutes dans Aplusix.

Les traces enrichies sont également enregistrées sous forme de fichiers textes. Ces fichiers ont une forme suivant les mêmes principes généraux (entête, format des enregistrements, enregistrements eux-mêmes), mais significativement plus complexes du fait de la richesse des informations enregistrées.

L’utilisation de fichiers textes lisibles et la forme de ces fichiers avec un entête, des pseudo-dtd locales exprimant la forme des données, puis les données elles-mêmes peuvent faire penser au langage XML. Les qualités de lisibilité, de formatage, d’auto-description sont communes. Pour autant, XML n’a pas été choisi pour représenter nos traces. Même si dans un futur proche, ces traces pourraient être « XMLisées », dans la mesure où l’on aura acquis les compétences nécessaires, dans l’immédiat, la question de leur taille et la maîtrise imparfaite de ces technologies XML, nous font préférer le format csv. En effet, pour ce qui concerne la taille des fichiers, un élément important relativement aux problématiques de stockage et de traitement des données, en adoptant XML, il est fort probable que la taille des fichiers augmentera d’un facteur multiplicatif important, 20 ou plus, les expressions mathématiques, en particulier, étant très gourmandes en place. Par ailleurs, concernant l’écriture normalisée d’expressions mathématiques, l’utilisation d’XLM, de MathML, d’OpenMath ou de OMDoc, nous souscrivons aux avis de (Jipsen, 2005) qui prône une écriture simplifiée « the main aims of the ASCIIMathML syntax are: -- 1. close to standard mathematical notation -- 2. easy to read -- 3. easy to type » ainsi que de (Mavrikis, 2005) et exprimons nos inquiétudes au sujet des futurs usages et de la lisibilité immédiate des expressions mathématiques données à l’aide des formats verbeux de la famille XML dont les standards sont souvent si complets qu’ils permettent d’écrire des expressions qui n’ont aucun sens mathématique.

2.3.2. Représentation des traces en base de données

Une première tentative pour stocker les traces dans des bases de données a été entreprise en 2003. L’enjeu, au niveau technique, était un stockage exhaustif et massif de l’ensemble du contenu de l’ensemble des traces récupérées, ou à récupérer, dans les différentes expérimentations déjà effectuées ou à venir. L’objectif pratique était double. D’une part, nous souhaitions permettre de centraliser les données reçues d’expérimentations diverses pour des traitements à grande échelle, type fouille de données, classification automatique, clustering, pour des recherches en apprentissage automatique. D’autre part, nous voulions permettre une approche plus statistique et globalisante pour des études didactiques ayant une culture plus proche des sciences de l’éducation, et des études didactiques internationales.

Pour les aspects techniques, le résultat a été positif : en laboratoire, traces brutes et traces enrichies sont aujourd’hui disponibles en base de données. Pour les aspects pratiques, le résultat est mitigé. Les études en apprentissage automatiques ont pu avoir lieu, mais sans appropriation de l’outil base de données par les didacticiens. La complexité cumulée des données et de la modélisation en base de données a renforcé l’emploi des fichiers textes simples, plutôt que de la structuration en base, sauf traitements spécifiques. Plusieurs raisons de ce semi échec peuvent être avancées. La première des raisons est donnée par la complexité du modèle de données décrivant ces traces cf. figure 3 : comportant plus de 30 tables, ce modèle de données n’est pas accessible aux non-informaticiens et reste difficile à appréhender pour des informaticiens non experts du domaine et spécialistes de bases de données. Une autre explication possible ressort, de notre point de vue, du niveau de granularité employé pour représenter les traces : la modélisation très fine qui a été employée, si elle relève bien de la philosophie base de données, n’est pas la plus adéquate pour représenter l’aspect linéaire et temporaire d’une trace d’activité. Enfin, l’accumulation de technologies a probablement nui à une plus grande utilisation de cette base.

Figure 3 : Extrait du modèle de données de la base de données de traces d’Aplusix

Une seconde tentative de modélisation avec une base de données a été entreprise récemment. L’objectif au niveau technique et pratique est plus modeste. Il ne s’agit que de stocker quelques éléments de traces enrichies pour centraliser l’influence des règles algébriques disponibles dans la bibliothèque de règles utilisée par l’algorithme de diagnostic, décrit en section 2.4. L’analyse des résultats de cette seconde démarche est en cours, l’expérience se poursuivant, l’appropriation de l’outil par les non-informaticiens ayant eu lieu.

2.4. Visualisation immédiate des traces brutes

Deux modules de l’environnement de base, disponibles en classe et en différé, reposent sur la trace. Ils permettent des utilisations, immédiates ou en différé, de celle-ci qui, si elles ne sont pas sans intérêt pédagogique ou pratique, ne nécessitent pas une puissance de calcul importante. Ces algorithmes reposent sur des algorithmes stables et relativement simples à mettre en place.

2.4.1. Magnétoscope de visualisation des traces brutes

Le premier module de l’environnement de base disponible en classe reposant sur la trace est un module de lecture et visualisation de la trace brute reprenant la métaphore du magnétoscope.

Pour l’essentiel, le magnétoscope sert aux chercheurs en didactique des mathématiques lors de leur analyse fine des comportements d’élèves. En particulier, comme il a été dit précédemment, les didacticiens sont fort intéressés par l’accès qu’ils obtiennent ainsi au brouillon de l’élève, à la zone privée de son travail où se trouvent les essais, les tentatives, les explorations, même celles, infructueuses, qui seront effacées après avoir été abandonnées. Cependant, il nous a également été signalé des activités effectuées au Canada avec des élèves utilisant le magnétoscope pour pratiquer une forme d’auto-évaluation de leur travail proche de la phase d’autocorrection proposée dans Aplusix après une phase de test (les usages de la phase d’autocorrection d’Aplusix n’ont pas été repérés).

Figure 4 : Magnétoscope d’Aplusix

Techniquement, le magnétoscope, permet de visualiser l’activité de l’élève, en respectant la ligne de temps (ou non, selon le choix de l’utilisateur), telle qu’elle a été observée lors de l’enregistrement. La forme graphique et les éléments non enregistrés dans la trace, mais (re)calculables, sont produits à la volée. Par commodité, pour faciliter la lecture de ces enregistrements lors de l’affichage avec le magnétoscope, les feedbacks indiquant l’équivalence entre étapes successives et la justesse de la solution sont donnés (même lorsqu’ils n’étaient pas montrés à l’écran initialement conformément aux paramètres d’affichage de l’environnement au moment de l’utilisation).

2.4.2. Éléments d’analyse statistique de l’activité élaborés immédiatement à partir de la trace brute

Une autre utilisation immédiate des traces est donnée par l’outil d’analyse statistique disponible dans les classes. Après sélection de la population concernée (délimitée par l’espace temporel et les étudiants), il est possible d'afficher les informations suivantes, qui sont obtenues par une analyse statistique sommaire des traces :

- Nombre d’exercices traités (total, moyenne ou écart type)

- Nombre d’exercices bien résolus (idem)

- Nombre de calculs erronés (idem)

- Score (idem)

- Temps passé (idem).

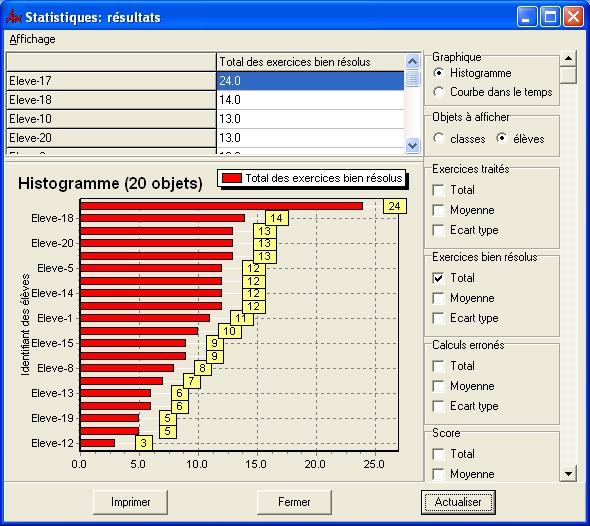
Lorsque l’activité est en cours de passation, les informations affichées sont actualisées toutes les 30 secondes, ce qui permet d’observer l’évolution du travail effectué par les élèves et de pratiquer un suivi de la séance (les usages du module de statistique n’ont pas été repérés).

Figure 5 : Suivi des élèves via les statistiques (élèves anonymés)

Ces deux modules offrent une lecture des traces brutes, sans interprétation cognitive de ce que fait l’élève. Or, nous avons pour objectif d’approcher les concepts et les processus mentaux mis en œuvre lors des transformations algébriques. Pour cela, nous avons cherché une modélisation locale de chaque pas de calcul d’élève donnant lieu à la production d’une trace enrichie représentant une interprétation plausible du travail de l’élève. À partir de celle-ci, nous construisons une modélisation globale visant à l’identification des conceptions à la source des comportements des élèves. Ces deux modélisations font l’objet des sections suivantes.

3. Définition d’un diagnostic local pour l’obtention d’une trace enrichie

3.1. Méthodologie de travail pour la définition d’un diagnostic local et l’obtention d’une trace enrichie

La modélisation locale recherchée consiste à découper chaque pas de calcul d’élève en une suite de pas de calcul élémentaires et d’associer une règle algébrique à chaque pas de calcul élémentaire. Un pas de calcul d’élève peut ainsi être interprété comme la succession d’applications de règles algébriques, cf. Tableau 1.

Tableau 1 : Exemple d'association d'une séquence de règles à un pas de calcul

La mise au point de cette modélisation locale comporte trois phases :

- Construction d’expérimentations pour recueillir une quantité importante de protocoles sous la forme de traces brutes. D’une part, celles-ci permettent d’étudier en différé les comportements habituels des élèves avec le magnétoscope. D’autre part, ces traces sont utilisées comme données de référence lors de la mise au point du diagnostic.

- Détermination à la main des règles, correctes ou erronées, qui sont appliquées par les élèves afin d’élaborer une bibliothèque de règles algébriques.

- Construction, automatisation et réglage fin d’un processus de diagnostic local associant à chaque pas de calcul d’un élève l’application d’une suite de règles algébriques de la bibliothèque.

Cette approche, par construction de bibliothèques de règles, est classique, on la retrouve chez (Wenger, 1987), mais elle est complexe et délicate. Elle est décrite en détail dans la section suivante, pour mettre en évidence l’apport et l’importance de l’emploi de traces brutes issues d’expérimentations en milieu écologique dans le processus global. Notons, cependant, que ce travail n’est pas nécessaire dans certains EIAH où il est demandé à l’élève de préciser (à l’aide d’un menu) la règle qu’il souhaite appliquer. Ainsi en est-il des environnements MathXpert (Beeson, 1998) ou T-algebra (Prank et al., 2006). Dans les deux environnements, les règles proposées à l’élève dépendent de l’expression qu’il souhaite transformer. Dans MathXpert, la règle est automatiquement appliquée tandis que dans T-algebra, le résultat est écrit par l’élève (lorsque l’environnement est en mode « libre »). Quoiqu’il en soit, le degré d’initiative de l’élève dans ces environnements est limité et l’opportunité d’apparition de certaines erreurs est nettement restreinte, nous éloignant du processus mental réel de l’élève. Les informations recueillies dans l’environnement Aplusix sont plus proches du chemin de pensée de l’élève, puisque ce dernier est libre d’écrire l’expression qu’il souhaite mais, en contre-partie, la modélisation de l’élève est plus complexe.

3.2. Expérimentations mises en place pour le recueil de traces brutes

Depuis 2003, nous avons conduit des analyses de protocoles individuels sur différentes populations d’élèves visant à construire, à partir de l’observation, un modèle qui permet, idéalement, de simuler les comportements.

Les expérimentations utilisées pour la recherche de régularités de comportements sont centrées sur des sous-domaines de l’algèbre tandis que les expérimentations construites dans le but de diagnostics locaux concernent un large champ d’exercices. Ces dernières ont eu lieu dans des classes de 4^e, 3^e, 2^nde et de 1^re. Leur organisation pouvait différer par le contenu ou par le mode d’encadrement. Elles devaient répondre à une double condition :

- recueillir des données caractérisant l’état de connaissances des élèves. Cela impliquait que les élèves soient plongés dans un cadre de travail consciencieux, qu’ils travaillent individuellement, sans intervention extérieure. À cette fin, une version spéciale du logiciel Aplusix a été utilisée pour restreindre l’ensemble des commandes et des rétroactions. Les enseignants participant aux expérimentations avaient pour consignes de ne pas apporter d’aide mathématique aux élèves, afin de répondre à cette première exigence.

- Couvrir la quasi-totalité du champ de problèmes de l'algèbre élémentaire des niveaux concernés : factorisation, réduction, développement, résolution des équations du premier degré, calculs numériques sur les fractions, mais aussi résolution d’inéquations, systèmes d’équations, etc. Nous ne souhaitions pas nécessairement, dans ce premier type d’expérimentation, obtenir des données nombreuses et cohérentes sur un même élève. Il nous importait, avant tout, d’avoir un grand nombre de données, quel qu’en soit l’auteur, dans toutes les activités susnommées. Un des fichiers d’exercices élaboré pour ce type d’expérimentations est accessible dans (Sander et al., 2005). La progression choisie consistait à changer de type d’exercice à chaque fois pour minimiser l’apprentissage.

Les protocoles de cet ensemble d’expérimentations ont permis de débuter l’élaboration de la bibliothèque des règles.

3.3. Élaboration de la bibliothèque de règles algébriques

Les règles algébriques sont des modélisations des observables (transformations effectuée par l'élève) ; elles sont des interprétations des comportements locaux. Une bibliothèque de règles correctes a été mise en œuvre très tôt dans Aplusix (dans une version non encore distribuée) pour effectuer des résolutions et faire des suggestions. Les règles erronées constituent une extension de cette bibliothèque.

3.3.1. Processus d’élaboration de la bibliothèque de règles erronées

La bibliothèque de règles erronées s’est construite en trois étapes décrites dans les paragraphes suivants :

- détection manuelle de règles détaillées erronées via le magnétoscope,

- regroupement des règles détaillées en règles abstraites,

- validation des choix précédents et suppression de certaines règles détaillées. Cette étape s’effectue par comparaison des diagnostics obtenus en prenant différentes bibliothèques de règles, la trace brute servant de données de référence.

Il y a, dans ce travail, une recherche de compromis entre richesse des traces, choix didactiques et contraintes informatiques.

L’identification des règles détaillées s’est faite manuellement. Elle repose sur des connaissances algébriques des didacticiens de notre équipe et sur l’étude fine des traces à l’aide du magnétoscope d’Aplusix (section 1.4.1). Le magnétoscope est, dans ce travail, essentiel. En particulier, il permet d'avoir accès à la sphère privée de l'élève, plus que ne le permettent les protocoles ou même le cadre papier/crayon : ce que l'élève accepte comme étape intermédiaire, visible aussi dans les traces enrichies, mais surtout ce qu'il efface, sont autant d'éléments précieux et apportent des précisions considérables quant aux modélisations des transformations. Quelques interviews d’élèves ont aussi permis de valider ou de préciser nos hypothèses d’interprétation. Par exemple, le pas de calcul de factorisation (7 + x)(x + 1) + (x + 1) —› (x + 1)(7 + x) a été expliqué par son auteur de la manière suivante : le deuxième facteur est complété par « ce qui reste dans chaque terme, en enlevant le facteur commun » ; dans le premier terme, « il reste (7+x) », dans le second, « rien ». Cette interview a validé la règle de factorisation que l’on avait choisie d’associer à cette transformation : ab + a —› a(b). Par des va-et-vient réguliers entre ces trois représentations des connaissances des élèves (pas de calcul, brouillon et interview), nous construisons une première trame de règles. Étant donnée la lourdeur du travail manuel, et la perspective d’atténuer cette lourdeur par la construction d’un diagnostic automatique, nous n’avons analysé manuellement que les traces recueillies dans certaines classes (principalement des classes de 4^e et 3^e, niveaux susceptibles de déceler plus d’erreurs conceptuelles). Nous avons ensuite généralisé les règles repérées manuellement. 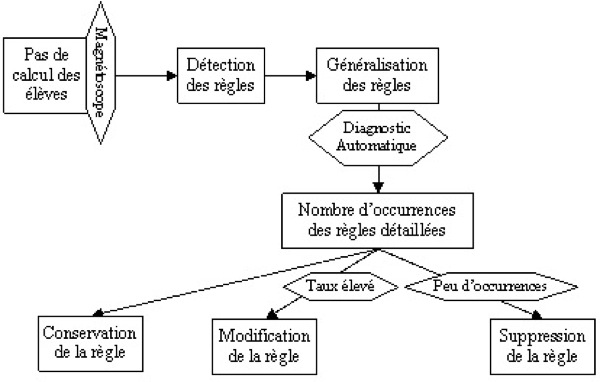Par exemple, l'erreur consistant à distribuer le signe moins uniquement sur les termes positifs revenait souvent : – (3x – 7x + 8 – y) —› – 3x – 7x – 8 – y ; la transformation consistant à ne distribuer le signe moins que sur les termes négatifs du type
– (3x + 2 – 7x) —› 3x + 2 + 7x paraissait alors tout aussi envisageable et nous l’avons intégrée comme une transformation possible, même si elle était absente des classes considérées³. À charge au diagnostic automatique de révéler si cette erreur se manifestait dans d’autres classes.

Des règles détaillées ont ensuite été regroupées en règles abstraites, selon le genre de tâches. Deux objectifs principaux organisaient ce travail : minimiser le nombre d’objets à traiter dans le processus automatique et faire ressortir des aspects cognitifs dans l’utilisation conjointe des règles. Par exemple, il est cognitivement intéressant de regrouper l'erreur consistant à appliquer la règle a+(b+c)—›a+b+a+c de la règle correcte de développement d’un produit a(b+c)—›ab+ac. Ces deux règles détaillées donnent la règle abstraite a≤(b+c)—›a≤b+a≤c où ≤ peut valoir + ou ×, règle qui, elle-même, pourrait être encore généralisée. Un exemple plus détaillé du travail d’abstraction est expliqué ci-après pour le genre de tâche mouvement (section 2.3.2). Ce sont, cependant, les règles détaillées qui sont associées aux pas de calcul d’un élève.

De manière conjointe, nous automatisons le processus de diagnostic qui permet de déceler le nombre d’applications d’une règle détaillée et d’en démontrer la pertinence. Après avoir listé, généralisé et codé un premier ensemble de règles à partir de centaines de transformations, le processus automatique (section 2.4) est lancé sur un nombre conséquent de transformations (de l’ordre du millier). Le diagnostic automatique permet de préciser le nombre d’occurrences de chaque règle. Étant donné que les règles n’ont d’intérêt que si on les observe chez un certain nombre d’élèves, nous supprimons ou modifions celles qui apparaissent marginalement. Pour des raisons informatiques (risque d’explosion combinatoire), nous tenons aussi compte du rapport du nombre d’applications d’une règle par le nombre de ses occurrences. Si ce taux est trop élevé, la règle s’applique souvent de façon inutile ; nous pouvons chercher à ajouter des conditions liées au contexte, dont la forme du but, pour l’appliquer moins souvent. Ce processus est décrit dans la figure 6.

Figure 6. Élaboration de la bibliothèque de règles

Progresser le long d'une spirale composée de l’identification manuelle des règles, et de l’analyse des résultats du diagnostic automatique a demandé plusieurs centaines d’heures de travail de didacticiens et d’informaticiens. Le résultat est l’obtention d’une bibliothèque de règles de calcul algébrique non marginales utilisées par les élèves aussi exhaustive que possible pour l’algèbre de 4^e-3^e.

3.3.2. Étude de cas : une règle unique pour le mouvement dans les équations et inéquations de degré 1

Le cas qui relève du genre de tâche « mouvement dans les équations et inéquations » montre l’évolution du travail d’élaboration de la bibliothèque. Les règles erronées détectées manuellement, combinées aux règles correctes, ont permis de faire émerger l’idée d’une seule règle abstraite, dite « règle de mouvement ».

La stratégie principale de résolution des équations de degré 1 consiste à développer les deux membres, le cas échéant, puis à isoler la variable en utilisant des théorèmes permettant d’effectuer des opérations sur les deux membres :

On ne change pas les solutions d'une équation en ajoutant ou en retranchant un même nombre aux deux membres de l'équation.

On ne change pas les solutions d'une équation en multipliant ou en divisant par un même nombre non nul les deux membres de l'équation.

Ces théorèmes produisent des règles (correctes) d’opérations sur les deux membres suivantes :

Règle 1: A=B —› A+C=B+C     

Règle 2: A=B —› A-C=B-C

Règle 3: A=B —› AC=BC (C≠0) 

Règle 4: A=B —› A/C=B/C (C≠0)

L’application de ces règles se combine à des réductions, ce qui donne naissance à des règles compilées plus efficaces (Anderson, 1983). La règle 2 produit la règle 5 : A+C=B —› A=B-C et la règle 6 : C=B —› 0=B-C. Dans ces règles, C est enlevé d’un membre pour être placé dans l’autre. Nous parlons de « mouvement », plus précisément de mouvement additif (correct) ici. À côté de ces deux règles de mouvement additif de gauche vers la droite, il faut ajouter deux règles (règles 7 et 8) de mouvement additif de droite vers la gauche. De façon analogue, la règle 4 produit la règle 9 : AC=B —› A=B/C (C≠0) et la règle 10 : C=B —› 1=B/C (C≠0). Nous parlons ici de mouvement multiplicatif de C. Ces règles doivent être complétées par des règles dans lesquelles le membre de gauche est une fraction, C étant le numérateur ou un facteur du numérateur, puis par les règles semblables de droite vers la gauche. De même, la règle 3 produit des règles de mouvement multiplicatif d’un terme pris au dénominateur.

Pour les inéquations, les règles effectuant un mouvement multiplicatif se dédoublent selon le signe de C. Par exemple, l’équivalent de la règle 9, pour la relation « < », est constitué de : AC<B —› A<B/C (C>0) et AC<B —› A<B/C (C<0).

On dénombre ainsi 20 règles correctes détaillées pour les mouvements dans les équations et 40 pour les inéquations.

Le nombre de règles erronées détaillées détectées dans les protocoles d’élèves travaillant sur des équations du premier degré se portent à 34 (Nicaud, 2005). En voici un exemple : AC = B —› A = B – C. La notion de mouvement est encore présente : l’argument C est passé d’un membre à l’autre. Cette notion de mouvement d’argument (terme ou facteur), correct ou erroné, suggère de regrouper l’ensemble de ces règles en une seule.

Pour cela, nous qualifions l’argument d’additif s’il se trouve dans une somme située dans un membre de l’équation ou s’il est lui-même un membre de l’équation. Quand le mouvement est effectué correctement, l’argument est encore additif, dans l’autre membre, et il a changé de signe syntaxique. L’argument est dit multiplicatif s’il se trouve dans une multiplication située dans un membre de l’équation. Dans ce cas, l’argument peut être « multiplicatif au numérateur », ce qui signifie qu’il est un facteur d’un membre de l’équation ou du numérateur d’une fraction qui est un membre de l’équation ; l’argument peut être « multiplicatif au dénominateur », ce qui signifie qu’il est un facteur du dénominateur d’une fraction qui est un membre de l’équation. Quand le mouvement est effectué correctement, l’argument est encore multiplicatif dans l’autre membre (au dénominateur s’il vient du numérateur et au numérateur s’il vient du dénominateur), il n’a pas changé de signe syntaxique, mais, dans le cas d’une inéquation, le sens de l’inéquation a changé si le signe sémantique (nombre positif ou négatif) de l’argument est négatif.

Nous pouvons maintenant décrire les mouvements (corrects ou erronés) avec une seule règle, intitulée Mouvement, à laquelle on associe un vecteur de sept variables, variables dont les noms sont indiqués ci-dessous, suivis des valeurs, exprimées à l’aide de noms symboliques, qu’elles peuvent prendre :

Symbole de relation : parmi (= ≠ < ≤ > ≥).

Position de l’argument à l’origine

- "PosOrgArgEstAdd" si la position d'origine de l'argument est additive.

- "PosOrgArgEstMult" si la position d'origine de l'argument est multiplicative.

Position finale de l’argument

- "PosFinaleArgEstAdd" : la position finale de l'argument est additive.

- "PosFinaleArgEstMult" : la position finale de l'argument est multiplicative.

Orientation horizontale du mouvement : parmi (GaucheDroite DoiteGauche).

Orientation verticale du mouvement : parmi (NumVersNum, NumVersDeno, NumVersDeno, DenoVersNum, DenoVersDeno), « Num » signifiant numérateur et « Deno » signifiant dénominateur.

Changement de signe de l’argument

- "ChangeSigneArg" : le signe de l'argument est changé lors du mouvement.

- "ChangePasSigneArg" : le signe de l'argument n'est pas changé.

Changement de sens

- "ChangePasSens" : le sens de l'inégalité n'est pas changé.

- "ChangeSens" : le sens de l'inégalité est changé.

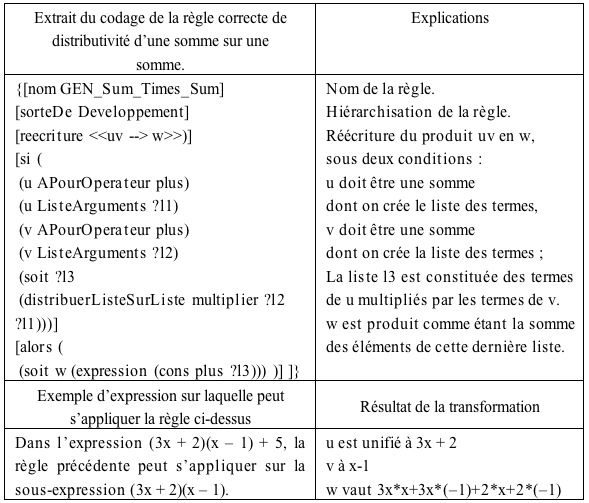
Par exemple, la transformation erronée 2x - 4 ≤ 5 —› 2x ≥ 5 - 4 est représentée par un Mouvement de -4 de vecteur : (≤, GaucheDroite, NumVersNum, PosOrgArgEstAdd PosFinaleArgEstAdd, ChangePasSigneArg, ChangeSens).

Les règles détaillées ne sont alors plus écrites comme les 54 (20 + 34) règles analysées a priori mais comme un vecteur, instanciation de la règle abstraite, soit 800 règles, produit d’une seule règle abstraite.

Les sept variables de ce vecteur sont en fait de deux types : celles qui décrivent l’expression initiale (les deux premières variables) et celles qui décrivent l’action (les cinq autres). Comme nous le réexpliquerons en section 3, les premières seront appelés variables de contexte tandis que les dernières, traits.

Il existe plusieurs types de règles. Leur distinction est décrite dans la section suivante.

3.3.3. Organisation et définition de trois types de règles

Nous distinguons trois types de règles, indépendamment du genre de tâche :

- Les règles détaillées de l’analyste. Elles sont au nombre de 1102.

- Les règles de mise en œuvre : les règles de l’analyste codées dans le langage opérationnel (Nicaud, 1993). Concrètement, une règle de mise en œuvre, R, est un mécanisme de transformation d'une expression A pour produire B. En ce sens, l'opérateur de raisonnement est « orienté », à la différence des identités habituelles du calcul algébrique, puisque B ne peut pas produire A, à moins qu'une règle inverse ne soit implantée. La règle R s'applique à une transformation E —› F si A peut être unifié à une sous-expression de E, cf. Tableau 2. Une règle de mise en œuvre peut produire plusieurs règles détaillées. Inversement, une règle détaillée nécessite parfois d’être écrite en deux règles de mise en œuvre. 257 règles de mise en œuvre ont été implantées qui recouvrent l’ensemble des activités algébriques au niveau 4^e-3^e.

- Les règles abstraites, classes de règles détaillées. Chacune organise un nombre important de règles attribuées aux élèves par l’analyste en un objet proche des règles utilisées par l’expert. C’est, entre autres, le cas de la règle du mouvement. 93 des règles de mise en œuvre ont été regroupées en 4 règles abstraites : mouvement, factorisation, réduction de deux arguments en un, distribution d’un opérateur, suppression brute de parenthèses.

Tableau 2 : Exemple de codage d'une règle de réécriture

3.4. Anaïs : Algorithme de diagnostic local basé sur une bibliothèque de règles

Un algorithme utilisant la bibliothèque de règles correctes et incorrectes, mettant en œuvre une recherche heuristique en chaînage avant, a été conçu et utilisé pour effectuer le diagnostic. Un logiciel, nommé Anaïs, mettant en œuvre cet algorithme, a été développé pour analyser les productions des élèves, enregistrées dans des bases de données. Il utilise, pour cela, les règles mises en œuvre, en tentant de trouver le meilleur enchaînement de ces règles entre deux expressions données, constituant un pas de calcul : la source et le but.

- Partant de la source, Anaïs développe un arbre en appliquant toutes les règles applicables à cette expression.

- L’application d’une règle produit un nouveau nœud et Anaïs construit ainsi, de proche en proche, un arbre de recherche, en choisissant, à chaque étape, un nœud à développer, le choix se faisant selon une heuristique tenant compte de la distance au but à atteindre.

- Lorsque le processus réussit, le but peut être atteint par plusieurs chemins. La sélection du meilleur chemin, comme résultat, se base sur un coût des chemins. Ce coût tient compte principalement du nombre de règles constituant le chemin. Différents chemins peuvent avoir le même coût, auquel cas, ils sont tous présentés comme des résultats, explications possibles du pas de calcul de l’élève. Les autres chemins (de coût plus élevé) sont conservés et présentés à la suite des « meilleurs » résultats.

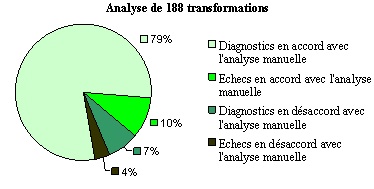
Le logiciel Anaïs découpe chaque pas de calcul de l’élève en une séquence d’étapes élémentaires sous la forme de règles. Il produit ainsi une trace enrichie sémantiquement et plus concise que la trace brute représentant une interprétation plausible de l’activité de l’élève.

Nous insérons, à l’aide d’un logiciel, les pas de calcul effectués par les élèves, issus des traces brutes, dans une base de données. Cela permet de faire des sélections de sous-ensembles de données sur lesquels nous étudions la pertinence du diagnostic. Par exemple, pour travailler sur les erreurs dans les équations, nous avons sélectionné les transformations erronées contenant un signe égal. La mise au point du diagnostic et de la bibliothèque de règles s’effectue ensuite en effectuant plusieurs essais. Une fonctionnalité de comparaison de diagnostics, permet de voir si la pertinence du diagnostic a progressé ou régressé entre deux sessions de diagnostics. Plus précisément, quand une règle est modifiée entre deux sessions, l’algorithme de comparaison entre sessions fait apparaître les pas de calcul qui ont été diagnostiqués différemment, l’expertise humaine peut alors choisir de garder ou non les modifications.

Les comparaisons de sessions ont souvent porté sur des bases de données d’environ 2000 pas de calcul erronés, une session durant environ 11 heures sur un ordinateur cadencé à 3 GHz. Etant donné qu’il est possible de lancer plusieurs Anaïs en parallèle, il est relativement rapide d’obtenir des résultats comparatifs.

3.5. Analyse des diagnostics locaux automatiques

Nous avons comparé les diagnostics automatiques à une analyse manuelle sur un ensemble de pas de calculs. Comparé à une analyse à la main, l’algorithme heuristique peut atteindre plus de 90% de satisfaction sur les diagnostics de pas de calcul corrects. Quant aux pas de calcul erronés, l’analyse s’est faite par genre de tâche. Par exemple, dans le domaine du développement et réduction d’expressions, l’analyse a porté sur une classe de 4^e et une classe de 3^e. Les 50 élèves de cette expérimentation ont effectué un total de 188 transformations erronées. 79% d’entre elles sont correctement diagnostiquées par Anaïs, voir figure 7. Le diagnostic automatique est en échec sur 14% des transformations : aucune séquence de règles n’a été trouvée. L’échec du diagnostic sur une transformation erronée peut, cependant, être en accord avec l’analyse manuelle si l’erreur est considérée comme marginale ou inexplicable, ce qui est le cas pour 10% des transformations diagnostiquées.

Figure 7 : Comparaison des diagnostics automatiques à l'analyse manuelle

4. Modélisation globale des connaissances de l’élève

Dans la section précédente, nous avons présenté une modélisation locale permettant de passer d’une trace brute d’activité d’élève à une trace enrichie. Décrite sous forme de règles diagnostiquées à partir des pas de calcul d'élèves, cette modélisation et ce niveau de traces ne permettent pas de comprendre le fonctionnement cognitif de l'élève au niveau des tâches algébriques. Pour cela, nous proposons de partir des règles diagnostiquées par Anaïs, de les regrouper et de les interpréter pour produire une modélisation des connaissances à un niveau supérieur : celui des tâches algébriques. Dans la suite, notre travail repose sur le découpage obtenu par le diagnostic local et les traces enrichies. Nous appelons dorénavant « pas de calcul », le pas de calcul élémentaire diagnostiqué par Anaïs, sans revenir au pas de calcul de l'élève.

4.1. Modélisation des activités algébriques transformationnelles

Un pas de calcul est décrit par une règle détaillée (section 2). Les règles détaillées présentent une certaine complexité, puisqu’elles se veulent très précises sur l’action faite par l’élève. Les règles détaillées peuvent être décrites en fonction des caractéristiques portant :

- soit sur l’expression initiale. Nous les appellerons variables de contexte : ce sont les éléments d’une expression algébrique pouvant avoir une influence sur le comportement de l’élève. Par exemple, la position de l’argument à l’origine dans un genre de tâche de mouvement.

- soit sur la transformation d’une expression en une autre. Nous les appellerons traits. Ce sont les différents « angles », sous lesquels peut être vue une règle détaillée. Par exemple, la transformation erronée d’une somme de deux monômes, axⁿ et bx^m, en un monôme, (a + b)x^n+m, peut être vue sous deux angles (traits) : d’une part, la transformation des coefficients a et b en un coefficient c. D’autre part, la transformation des degrés n et m en un degré p. Le trait « coefficient » prend, dans notre exemple, la valeur « somme des coefficients initiaux » (a + b) et le trait degré, la valeur « somme des degrés initiaux » (n + m). Quant à la règle détaillée de la section 2.3.2 concernant le genre de tâche « mouvement », nous obtenons trois traits : le signe, l’opérateur, et le sens.

Pour réduire la complexité d’une règle détaillée, nous projetons la règle selon l’un des traits : nous définissons un Vecteur du Comportement Local selon un trait T, que nous notons VCL(trait), comme le vecteur constitué, d’une part, des variables de contexte de la règle détaillée et, d’autre part, de la valeur du trait T. Par suite, à une règle détaillée, nous associons autant de VCL(trait) que la règle a de traits. Par exemple, à chaque pas de calcul de « mouvement », nous associons trois VCL : le VCL(signe de l’argument), le VCL(opérateur de l’argument), le VCL(sens de l’inéquation). Le dernier trait n’existant que si la variable de contexte « symbole de relation » prend la valeur inéquation.

Les VCL proposent un découpage et une réorganisation des faits relevés par un observateur. Il s'agit d'un niveau comportemental de la modélisation de l’élève (Wenger, 1987), (Dillenbourg & Self, 1992). Le choix des événements qui doivent être pris en compte pour ce niveau est le résultat des décisions de l'observateur, comme le souligne (Balacheff, 1994), p. 26, « la modélisation comportementale exige donc un premier niveau d'interprétation, celui de l'organisation du réel ».

Notre méthodologie générale pour l’obtention d’une modélisation globale repose sur deux axes qui se développent en étroite interaction :

Axe 1 : Construction du modèle

Il s'agit de trouver un moyen de découper le réel et de l'organiser en vue de caractériser les comportements des élèves en termes de théorèmes-en-acte. La construction se fait autour des points suivants :

- distinguer les variables de contexte des traits au sein des règles détaillées fournies par le diagnostic automatique,

- réaliser des expérimentations spécifiques pour affiner et valider le modèle,

- regrouper des règles détaillées en traits, caractériser les règles d'action, et les théorèmes-en-acte.

Une de difficultés de la modélisation est de trouver un niveau de granularité pertinent pour les interprétations. En effet, plus il est fin, mieux il permet de rendre compte du contexte, mais plus il risque de cacher les régularités entre le contexte et les actions.

Axe 2 : Construction du mécanisme de diagnostic

Il s'agit d'implanter le modèle au niveau informatique et plus précisément :

- de construire un mécanisme permettant de diagnostiquer, pour chaque trait, les VCL stables selon des critères de stabilité à définir. Les VCL stables correspondent aux règles d'action de (Vergnaud, 1991),

- de construire un mécanisme qui permet de regrouper les règles d'actions sous forme de théorèmes-en-acte, (ibid.),

Cette méthodologie a été mise en œuvre uniquement pour le genre de tâche « mouvement ». Pour les autres genres de tâches, les recherches sont en cours.

4.2. Étude de cas

Dans cette partie, comme dans la section 2.3.2, nous illustrons la méthodologie décrite ci-dessus à travers l'étude de cas sur le genre de tâche « mouvement ».

4.2.1. Description des VCL(trait)

Nous présentons ci-dessous les VCL(trait) pour les trois traits du mouvement. Ces vecteurs sont décrits par (Nom du vecteur ; variables de contexte instanciées ; Action). Les variables de contexte, comme nous l’avons abordé en section 2.3.2, sont au nombre de trois :

- type de relation : Eq (pour équation) ou Ineq (pour inéquation) ou vide,

- position d'origine de l’argument : Add (pour additif), Mult (pour multiplicatif), Num (pour numérateur) ou Deno (pour dénominateur),

- signe de l'argument : plus ou moins.

Nous obtenons les trois vecteurs de comportements locaux (VCL) :

- VCL(signe) = (VCLP-Signe-X ; Type de relation, Position de l'argument à l'origine, Signe de l'argument ; Action sur le signe). Rappelons que les actions possibles sur le signe (cf. section 2.3.2) sont : ChangeSigneArg (le signe de l'argument est changé) et ChangePasSigneArg (le signe de l'argument n'est pas changé). On obtient 16 valeurs possibles de ce vecteur dont 8 expriment des règles correctes,

- VCL(sens) = (VCLP-Sens-X ; inéquation, Position de l'argument à l'origine, Signe de l'argument ; Action sur le sens). Rappelons que les actions possibles sur le sens (cf. section 2.3.2) sont ChangePasSens (le sens de l'inégalité n'est pas changé), ChangeSens (le sens de l'inégalité est changé). On obtient 8 valeurs possibles de ce vecteur dont 4 expriment des règles correctes,

- VCL(opérateur) = (VCLP-Opérateur-X ; Type de relation, Position de l'argument à l'origine, Signe de l'argument ; Action sur l'opérateur). Rappelons que les actions possibles sur l’opérateur (cf. section 2.3.2) sont : Additif (l'argument est additif dans la position finale (a+x)), Multiplicatif-Numérateur (l'argument est multiplicatif au numérateur dans la position finale (a*x)), Multiplicatif-Dénominateur (l'argument est multiplicatif au dénominateur dans la position finale (x/a)). On obtient 18 valeurs possibles de ce vecteur, dont 6 expriment des règles correctes.

Un VCL(trait) est une projection de la règle détaillée. En cela, il y a perte d’informations entre la règle détaillée et l’interprétation du VCL(trait). Par exemple, le vecteur (VCLP-Signe-1a equation PosOrgArgEstAdd SigneArgEstPlus ChangePasSigneArg) peut être interprété par la règle : « Si l'argument à déplacer, d'un membre d'une équation à l'autre membre, est en position additive et de signe positif, alors on ne change pas de signe après le mouvement », ou encore « si a+b=c alors b=c¤a ou b=a¤c où ¤ désigne un opérateur parmi +, *, / » tandis que la règle détaillée précise quel est l’opérateur final.

4.2.2. Détermination et organisation a priori des théorèmes-en-actes

Pour chaque trait de la tâche « mouvement », nous avons défini des théorèmes-en-acte globaux (TeA globaux) (cf. annexe A). Un TeA global est un ensemble d’actions de même type, quelque soit le contexte. C’est-à-dire une utilisation régulière du même VCL(trait) dans différents contextes. Pour le trait « signe », les TeA globaux sont au nombre de cinq. Par exemple, le TeA global « Conservation du Signe » signifie que quelque soit les valeurs prises par les trois variables de contexte (type de relation, position et signe de l’argument), le signe n’est jamais modifié lors d’un mouvement d’argument. Ce TeA est parfois correct ou incorrect selon les valeurs prises par les variables de contexte, comme nous le réexpliquerons ci-après.

Ces théorèmes-en-acte globaux peuvent être particularisés selon que l’on fixe la valeur d’une, de deux ou de trois des trois variables de contexte. Si aucune variable de contexte n’est fixée, le contexte est donc général, on obtient les TeA globaux eux-mêmes, que l’on nomme aussi TeA de profondeur 0. Si une seule variable est fixée (respectivement deux, respectivement trois), la profondeur du TeA est de 1 (respectivement 2, respectivement 3). La profondeur 3 correspond aux règles d’actions, décrites ci-dessous (ce sont des VCL(trait) qui ont montré une certaine stabilité). Cela forme une hiérarchie de TeA en forme de treillis dont les racines sont les TeA globaux, chacun ayant des descendants, et dont les feuilles sont les règles d’action, comme indiqué sur les treillis présentés en annexe B. Nous appellerons contexte un triplet de valeurs des trois variables. Nous appellerons théorèmes-en-actes (TeA) une des quatre décompositions possibles des TeA globaux.

Par exemple, le TeA « Conservation du Signe » lorsque la variable type de relation prend la valeur équation (« Eq »), signifie qu’il y a conservation du signe de l’argument dans le mouvement d’une équation, quelque soit les valeurs prises par les variables position et signe de l’argument. Ce TeA est de profondeur 1. Le nom associé à ce TeA est le nom du TeA global dont il dépend suivi des valeurs fixées des variables. Pour cet exemple, le TeA est nommé « Conservation du Signe- Eq ».

Selon la profondeur, le TeA peut être correct, c'est-à-dire correspondant à une règle algébrique correcte, ou incorrect. Un TeA est correct s’il est diagnostiqué directement à partir des VCL corrects ou si tous ses descendants sont corrects. Dans ce cas, son domaine de validité est le contexte dans lequel il est défini (cf. les treillis en annexe B) : les TeA corrects sont représentés en clair.

Dans les autres cas, le TeA est incorrect pour le contexte où il est défini, dans la mesure où un ou plusieurs de ses descendants sont des TeA incorrects. Cependant, son domaine de validité n’est pas nécessairement vide, il est constitué de l’ensemble des domaines de validité de ses descendants.

Par exemple : le TeA « conservation de l'opérateur » qui consiste à reporter le même opérateur dans l'autre membre, n'est pas correct dans le contexte le plus général. Son domaine de validité est le contexte additif (c’est-à-dire lorsque la variable « position » d’origine de l’argument prend la valeur « additif »).

4.2.3. Détermination des théorèmes-en-acte

Dans ce paragraphe, nous nous limitons au trait « signe ». Le diagnostic des théorèmes-en-acte se fait en deux étapes, à la suite du diagnostic local en commençant par un mécanisme de calcul type overlay, et en se poursuivant par un algorithme de généralisation.

Étape 1 : Détermination automatique des VCL stables.

Nous définissons les règles d'action par un VCL(trait) stable. Nous définissons stable par le fait que l'élève a le même comportement, c’est-à-dire la même valeur du trait, à chaque fois qu'il se trouve dans un contexte donné. Etant donné que l’élève n’a pas toujours un comportement stable, il faut déterminer quel est la valeur du trait qui représente le mieux son comportement. Ainsi, pour le trait « signe », deux valeurs sont possibles (le signe est changé et le signe n’est pas changé, cf. section 3.2.1), il faut déterminer parmi ces deux valeurs celle qui est la plus utilisée par un élève et « combien » elle est utilisée.

À une liste de k pas de calcul d’élèves concernant la tâche « mouvement » est associée la liste des k règles détaillées du diagnostic local. De là, nous construisons la liste des k VCL(signe) (respectivement, VCL(opérateur), etc.). Pour un contexte, nous étudions la stabilité des VCL correspondants. Par exemple, pour le contexte (Equation, PosOrgArgEstAdd, SigneArgEstPlus), il y a n VCL(signe). Soit n₁, le nombre d’occurrences de VCL qui ont pour valeur de trait ChangePasSigneArg et n₂, le nombre d’occurrences de VCL qui ont pour valeur de trait ChangeSigneArg (n₁ + n₂ = n). Le rapport n₁/n est appelé coefficient du VCL.

Nous attribuons trois statuts aux données par rapport au contexte :

- insuffisantes si n≤ 3,

- suffisantes-instables si n≥4 et (n₁/n ≤ 0.75 et n₂/n ≤ 0.75),

- suffisantes-stables si n≥4 et (n₁/n ≥ 0.75 ou n₂/n ≥ 0.75).

Dans le premier cas, nous n'avons pas suffisamment de données pour produire un diagnostic sur les connaissances de l'élève. Dans le deuxième cas, nous avons des données significatives mais elles ne permettent pas de déterminer une corrélation entre le contexte et les actions. Enfin, le troisième cas nous permet de faire l'hypothèse d’une certaine stabilité du comportement de l'élève et nous pouvons donc déduire une corrélation entre le contexte et l'action dont le nombre d'occurrences est le plus grand. Par exemple, si pour le contexte (Equation, PosOrgArgEstAdd, SigneArgEstPlus) il y a des données suffisantes-stables avec n₂ majoritaire, nous diagnostiquons une corrélation entre ce contexte et l'action ChangeSigneArg, et nous considérons Le VCL(signe) (Equation, PosOrgArgEstAdd, SigneArgEstPlus, ChangeSigneArg) comme un comportement pertinent pour le diagnostic des théorèmes-en-acte, car il exprime une régularité dans le comportement de l'élève. En fait ce comportement pertinent diagnostiqué est une règle d'action, au sens défini plus haut.

Étape 2 : Détermination automatique des théorèmes-en-acte et généralisation.

La construction des TeA se fait par association de règles d’action ayant une valeur de variable de contexte commune. Par exemple si les deux VCL (Equation PosOrgArgEstMult SigneArgEstPlus ChangePasSigneArg) et (Equation PosOrgArgEstMult SigneArgEstMoins ChangeSigneArg) ont montré une certaine stabilité, ils ont alors été diagnostiqués comme des règles d’action. Leur utilisation conjointe par un même élève contribue à lui associer le TeA « ValeurAbsolue-Equation-Multiplicatif », qui signifie que l’élève conserve le signe de l’argument quand il effectue un mouvement dans une équation et que la position d’origine de l’argument est « multiplicatif ».

Un coefficient est associé aux TeA se trouvant en conclusion de ces règles pour évaluer la validité. Il est calculé comme la moyenne géométrique des coefficients des VCL. Lorsque le passage des VCL aux TeA est réalisé, une propagation des coefficients est effectuée dans les hiérarchies de TeA. Les coefficients associés aux VCL et aux TeA sont des formes de facteurs de certitude (Buchanan & Shortliffe, 1984). Les TeA qui sont produits comme résultats du processus sont ceux qui ont le contexte le plus large, c’est-à-dire qui sont les plus hauts dans la hiérarchie. En d’autres termes, si un TeA T1 est élu et si son père T2 est aussi élu, T1 n’est pas présenté comme résultat car il est inclus dans T2. Ce processus permet d'obtenir un modèle de l'élève sur chaque trait, comme le montre l'exemple ci-dessous pour le trait signe.

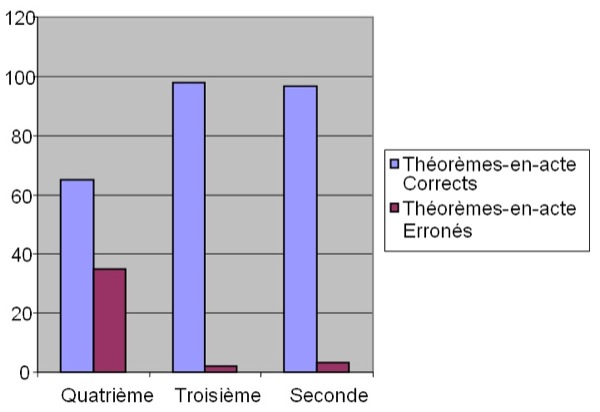
Tableau 3. Extrait d'un modèle de l'élève. Les cinq premières lignes donnent les résultats du diagnostic des VCL (nom du VCL suivi des variables de contexte, de l'action et du nombre d'occurrence du VCL pour un élève). Les trois dernières lignes sont des diagnostics des théorèmes-en-acte de l'élève (nom du TeA et son coefficient associé) obtenus à partir des VCL ci-dessus.

4.2.4. Résultats

Nous avons mis en place des expérimentations pour déterminer les théorèmes-en-acte des élèves relatifs au changement de signe dans les équations, selon le modèle décrit ci-dessus. Les exercices ont porté sur des équations et inéquations dont la résolution nécessite des mouvements additifs et multiplicatifs d’arguments qui peuvent être de signe "+" ou "–". Pour ne pas mettre les élèves en difficulté sur des tâches qui ne concernent pas directement les théorèmes-en-acte sur les mouvements, nous avons choisi des exercices avec des coefficients entiers et avec des développements simples.

Ces expérimentations étaient réalisées auprès de 3186 élèves, dont 2503 élèves brésiliens et 683 élèves français. La répartition de l'ensemble des TeA relatifs au « Signe dans le mouvement » pour ces élèves est donnée en annexe C. Nous constatons que 13,7% des TeA sont erronés et qu’ils concernent essentiellement les contextes Multiplicatif ou Inéquation.

Nous avons analysé l'évolution des TeA des élèves français entre les niveaux 4^e, 3^e et 2^nd (cf. figure 8).

Figure 8 : Comparaison des TeA de la classe de 4^e et 3^e

Comme le montre la figure 8, entre la classe de quatrième et la classe seconde, le nombre d'élèves ayant un TeA erroné diminue en passant de 35% à 3% et le nombre d'élèves ayant un TeA correct augmente en passant de 65% à 97%. Cependant, si on examine l'évolution des TeA corrects entre ces deux niveaux, on constate qu'en classe de seconde les TeA corrects diagnostiqués sont plus dispersés par rapport au contexte que ceux de la classe de quatrième. En effet, le TeA SigneCorrect de niveau de profondeur 0 passe de 28.1% à 17,7% et les TeA corrects de profondeur 1 passent de 0 à 10% (pour SigneCorrect-Equation), 6.2% (pour SigneCorrect-Inequation) et 22.4% (pour Conservation-signe-Multiplicatif). De même, on a plus de dispersion des TeA corrects de niveau de profondeur 3 en classe de seconde qu'en classe de quatrième.

Ces résultats montrent que l'évolution des TeA corrects entre la classe de quatrième et seconde est accompagnée des dispersions des TeA corrects au niveau des contextes additif et équation.

5. Conclusion et perspectives

Les productions écrites des élèves constituent un des outils didactiques pour la modélisation des connaissances. Dans notre recherche, nous avons travaillé sur des données obtenues dans l'EIAH Aplusix. Des choix didactiques et informatiques ont été faits pour constituer des traces brutes que nous considérons comme étant le réel pour notre modélisation. Ce réel est constitué d'éléments de la résolution de problème, comme ceux obtenus dans l'environnement classique papier, mais aussi d'autres informations comme le temps, les hésitations, les corrections. Ces traces constituent une modélisation comportementale de l'élève.

Sur le plan didactique, nous nous intéressons à une modélisation épistémique de l'élève qui est une interprétation de ce qui se produit au niveau comportemental (Wenger, 1987). Celle-ci est faite dans un environnement informatique Anaïs qui procède, dans un premier temps, à une restriction, un découpage et une interprétation des traces brutes pour produire des traces enrichies. La restriction consiste à ne retenir que les éléments de la résolution de problème, les pas de calcul des élèves. Quant au découpage et à l'interprétation, ils se fondent sur l'ensemble des traces brutes pour associer manuellement puis automatiquement à un pas de calcul une séquence de règles algébriques. Percevoir un pas de calcul comme une séquence de règles algébriques est un premier niveau du modèle épistémique, car il permet de reproduire, mais aussi d'expliquer les pas de calculs. Ce modèle qui est local, ne tient compte ni de l'historicité des activités de l'élève ni de la stabilité de son comportement. Il est indépendant de l'élève et ne suffit donc pas d'un point de vue didactique. C'est pourquoi, dans un deuxième temps, nous avons cherché, chez un même élève, la stabilité de l'utilisation des règles, en identifiant le contexte où elles apparaissent, par la construction de Vecteurs Comportementaux Locaux. Puis, nous les avons regroupés selon un point de vue cognitif pour produire des théorèmes-en-actes. Ce deuxième niveau du modèle épistémique constitue une modélisation conceptuelle de l'élève et s’effectue à partir des traces enrichies produites au premier niveau du modèle épistémique. Ce travail s'est appuyé sur des analyses manuelles et automatiques d'expérimentions ayant eu lieu dans des établissements scolaires de différents pays. La confrontation de ces deux modes d'analyses a permis d'affiner les modèles tout en les validant.

Comme nous l'avons dit, la modélisation locale des règles est indépendante de l'élève. Ceci présente une faiblesse lorsque plusieurs diagnostics peuvent expliquer un même pas de calcul. Actuellement, le choix du « meilleur » diagnostic est fait de façon aléatoire. Pour pallier cette faiblesse, une prise en compte du passé de l'élève est envisagée, en intégrant dans un modèle probabiliste les règles précédemment diagnostiquées pour cet élève.

L'élargissement du traitement épistémique du genre de tâche « mouvement » aux quatre autres genres de tâche soulève de nouvelles difficultés dues à la quantité des règles et des variables de contexte décrivant ces genres de tâches. Nous examinons de nouvelles techniques basées en partie sur des considérations statistiques (Croset, 2007) qui permettent de déterminer des liens implicatifs entre variables de contexte et règles.

BIBLIOGRAPHIE

ANDERSON J.R. (1983). The Architecture of Cognition. Cambridge, MA: Harvard University Press.

BALACHEFF N. (1994). Didactique et intelligence artificielle. Recherche en Didactique des Mathématiques. p 9-42.

BEESON M. (1998). Design Principles of Mathpert: Software to support education in algebra and calculus. In: Kajler (ed.) Computer-Human Interaction in Symbolic Computation. Springer-Verlag, Berlin Heidelberg New York, p 89-115.

BUCHANAN B.G., SHORTLIFFE E.H. (1984). Rule-Based Expert Systems, The Mycin experiments of the Stanford Heuristic Programming Project. Addison-Wesley Publishing.

CHAACHOUA H., LIMA I. (2003). De la modélisation des conceptions des élèves à la prise de décisions didactiques par l'enseignant : le rôle d'un environnement informatique. Actes du colloque ITEM 2003, Reims.

CROSET M.-C. (2007). Prise en compte du contexte algébrique dans la modélisation des connaissances d’un élève. Le cas de la factorisation. Actes de la conférence EIAH 2007, Environnements Informatiques pour l'apprentissage Humain, Lausanne, Suisse (à paraître).

DE VICENTE A., PAIN H. (1998) Motivation Diagnosis in Intelligent Tutoring Systems, Proceedings of the 4th International Conference, ITS '98, LNCS 1452, San Antonio, Texas, USA.

DILLENBOURG P., SELF J. (1992). A framework for learner modelling. Interactive Learning Environments, Vol. 2, p 111-137.

JIPSEN P. (2005). Translating ASCII math notation to Presentation MathML, ASCIIMathML.js (verion 1.4.7). Disponible sur internet : http://www1.chapman.edu/~jipsen/mathml/asciimathsyntax.html

KIERAN C. (2001). The core of algebra: Reflections on its Main Activities. ICMI Algebra Conference, Melbourne, Australia, p 21-34.

MAVRIKIS M. (2005). MathQTI Draft Specification. Disponible sur internet : http://www.maths.ed.ac.uk/mathqti/docs/v0p3/mathqti_v0p3.pdf

NICAUD J.-F. (1993). SIM version 1.1, Manuel de Référence. Rapport du laboratoire LRI, n° 866.

Ouvrage collectif (2005). Modélisation cognitive d'élèves en algèbre et construction de stratégies d'enseignement dans un contexte technologique. Project report of the “Ecole et sciences cognitives” research programme. Cahier du laboratoire Leibniz n°123. Disponible sur internet : http://www-leibniz.imag.fr/.

NICAUD J.-F., BOUHINEAU D., CHAACHOUA H. (2004). Mixing microworld and CAS features in building computer systems that help students learn algebra. International Journal of Computers for Mathematical Learning, Vol. 9-2, p 169-211.

NICAUD J.-F., BOUHINEAU D., HUGUET T. (2002). The Aplusix-Editor: A New Kind of Software for the Learning of Algebra. Proceedings of the 6th International Conference on Intelligent Tutoring Systems, LNCS 2363, Biarritz, France and San Sebastian, Spain, p 178-189.

PRANK R., ISSAKOVA M., LEPP D., VAIKSAAR V. (2006). Using Action-Object-Input Scheme for Better Error Diagnosis and Assessment in Expression Manipulation Tasks. Maths, Stats and OR Network, Maths CAA Series. Disponible sur internet : http://mathstore.ac.uk/articles/maths-caa-series/mar2006/.

SANDER E., NICAUD J.-F., CHAACHOUA H., CROSET M.-C. (2005). From usage analysis to automatic diagnosis: the case of the learning of algebra. Proceedings of 12nd International Conference on Artificial Intelligence in Education (AIED 2005), Amsterdam, The Netherlands, IOS Press, p. 45-52.

TAHRI S. (1993). Modélisation de l'interaction didactique : un tuteur hybride sur Cabri-géomètre pour l'analyse des décisions didactiques, Grenoble, Université Joseph Fourier.

VERGNAUD G. (1991). La théorie des champs conceptuels. Recherches en Didactique des Mathématiques, Vol. 10/2.3, p. 133-170.

VERGNAUD G. (2001). Forme opératoire et forme prédicative de la connaissance. Conférence publiée dans les Actes du Colloque GDM-2001.

WENGER E. (1987). Artificial intelligence and tutoring systems, Morgan Kaufmann Publishers.

¹ Tiré de (Vergnaud, 1991).

² Kieran appelle transformationnelle, l’approche qui consiste à changer la forme d’une expression/équation en conservant l’équivalence. Elle rappelle que des approches uniquement générationnelle, ou de modélisation, ne permettent pas de donner à l’élève tous les sens de l’algèbre : transformer une expression en une autre équivalente permet de relier une tâche algébrique à une réflexion conceptuelle.

ANNEXE A : LES THEOREMES-EN-ACTE GLOBAUX

Les 5 TeA globaux du trait « Signe dans mouvement »

Les 4 TeA globaux du trait « Sens dans mouvement »

Les 5 TeA globaux du trait « Opérateur dans mouvement »

ANNEXE B : LES TREILLIS DES THEOREMES-EN-ACTE
DU TRAIT « SIGNE ».

Noms des théorèmes en acte globaux TeA

Théorèmes en actes sur des domaines plus restreints. TeA-x-y-z

x, y et z précisent le contexte parmi les valeurs suivantes :

- type de relation : Eq (pour équation) ou Ineq (pour inéquation) ou vide.

- position d'origine de l’argument : Add (pour additif), Mult (pour multiplicatif), Num (pour numérateur) ou Deno (pour dénominateur).

- signe de l'argument : plus ou moins.

ANNEXE C : REPARTITION DES TeA RELATIFS AU TRAIT SIGNE DANS LE GENRE DE TACHE MOUVEMENT POUR UNE EXPERIMENTATION SUR 3186 ELEVES

Répartition des TeA relatifs au « Signe dans Mouvement » par niveau de profondeur du contexte. %E désigne le pourcentage des TeA par rapport au nombre total d'élèves, %C désigne le pourcentage des TeA par rapport au nombre total de TeA. En gras, les TeA corrects.

A propos des auteurs

Hamid CHAACHOUA est maître de conférences à l’université Joseph Fourier à Grenoble, France. Il est docteur en didactique des mathématiques depuis 1997 et membre de l’équipe Metah du laboratoire LIG. Ses travaux portent sur la modélisation didactique et informatique de l’apprenant, ressources en ligne et intégration des TICE dans l’enseignement des mathématiques.

Adresse : Laboratoire LIG, 46, Avenue Félix Viallet, 38031 Grenoble Cedex, France

Courriel : Hamid.Chaachoua@imag.fr

Marie-Caroline CROSET est doctorante de troisième année au Laboratoire Informatique de Grenoble en Didactique des Mathématiques. Elle s’intéresse à la modélisation des connaissances des élèves en algèbre au sein d’un Environnement Informatique pour Apprentissage Humain.

Adresse : Laboratoire LIG, 46, Avenue Félix Viallet, 38031 Grenoble Cedex, France

Courriel : Marie-Caroline.Croset@imag.fr

Toile : http://www.noe-kaleidoscope.org/people/croset/

Denis BOUHINEAU est Maître de Conférences à l'Université Joseph Fourier, Grenoble-I et membre du laboratoire LIG (équipe METAH). Il a obtenu son doctorat en Informatique dans cette même université en 1997. Ses recherches actuelles portent sur la définition et la mise en oeuvre d'EIAH pour des situations actives d'apprentissage réellement utilisées à l'école.

Adresse : Laboratoire LIG, 46, Avenue Félix Viallet, 38031 Grenoble Cedex, France

Courriel : Denis.Bouhineau@imag.fr

Toile : http://www.noe-kaleidoscope.org/people/DenisB/

Marilena BITTAR est professeur à l'Université Federal de Mato Grosso do Sul au Brésil. Elle dirige des recherches sur la modélisation des connaissances des élèves en algèbre et sur la formation d'enseignants à l'usage des technologies.

Adresse : Universidade Federal de Mato Grosso do Sul – UFMS, Brésil

Courriel : marilena@nin.ufms.br

Jean-François NICAUD est professeur d’informatique à l’Université Joseph Fourier (Grenoble). Depuis 1983, ses recherches sur les EIAH ont été conduites successivement à Orsay, Nantes et Grenoble. Elles portent sur le domaine de l’algèbre : conception, développement et déploiement du logiciel Aplusix qui est actuellement distribué dans 8 pays, modélisation de l’élève avec des techniques de recherche heuristique. Il a organisé et présidé les journées EIAO de Cachan pendant 10 ans.

Adresse : Laboratoire LIG, 46, Avenue Félix Viallet, 38031 Grenoble Cedex, France

Courriel : Jean-Francois.Nicaud@imag.fr

Référence de l'article :

Hamid CHAACHOUA, Marie-Caroline CROSET, Denis BOUHINEAU, Marilena BITTAR, Jean-François NICAUD, Description et exploitations des traces du logiciel d’algèbre Aplusix, Revue STICEF, Volume 14, 2007, ISSN : 1764-7223, mis en ligne le 08/03/2008, http://sticef.org