 Sciences et Technologies
Sciences et Technologies de l´Information et
de la Communication pour
l´Éducation et la Formation
Volume 27, 2020
Article de recherche
Numéro Spécial
Sélection de la conférence
EIAH 2019

Reconnaissance de motifs redondants et répétitions : introduction à la Pensée Informatique
Yvan PETER (1), Yann SECQ (1), Marielle LÉONARD (1)(2)
(1) Univ. Lille, CNRS,
Centrale Lille, UMR 9189 CRIStAL, France
(2) CIREL, Centre Interuniversitaire de
Recherche en Éducation de Lille, EA 4354
![]() RÉSUMÉ : Cet
article présente une expérimentation d'initiation
d'élèves de primaire à la pensée informatique.
L'objectif est de développer la capacité de reconnaître des
motifs et de les exprimer sous la forme de répétitions via des
activités déconnectées et en ligne. Les résultats
montrent un impact positif des activités ainsi que les compétences
acquises.
RÉSUMÉ : Cet
article présente une expérimentation d'initiation
d'élèves de primaire à la pensée informatique.
L'objectif est de développer la capacité de reconnaître des
motifs et de les exprimer sous la forme de répétitions via des
activités déconnectées et en ligne. Les résultats
montrent un impact positif des activités ainsi que les compétences
acquises.
![]() MOTS CLÉS : Pensée
Informatique, Programmation, Séquence Pédagogique, École
primaire
MOTS CLÉS : Pensée
Informatique, Programmation, Séquence Pédagogique, École
primaire
![]() ABSTRACT : This
article presents an experimentation to introduce Computational Thinking to
primary school pupils. The aim is to enhance their capability to spot repetitive
patterns and to express them as loops through unplugged and plugged-in
activities. The results show a positive impact of the activities and the
competencies acquired.
ABSTRACT : This
article presents an experimentation to introduce Computational Thinking to
primary school pupils. The aim is to enhance their capability to spot repetitive
patterns and to express them as loops through unplugged and plugged-in
activities. The results show a positive impact of the activities and the
competencies acquired.
![]() KEYWORDS : Computational
Thinking, Programming, Pedagogical Sequence, Primary school
KEYWORDS : Computational
Thinking, Programming, Pedagogical Sequence, Primary school
1. Introduction
La pensée informatique (PI) correspond à des compétences d'abstraction et de résolution de problèmes qui peuvent être exploitées dans de nombreux contextes et appliquées à des domaines divers. La PI en tant que compétence cognitive ne se réduit pas à la programmation. Toutefois, elle vise à exprimer les choses d'une manière qui se prête à un traitement informatique. En ce sens, elle permet d'aborder la dimension algorithmique et la programmation en général. Dans son article fondateur, J. Wing appelle à l'enseignement de la pensée informatique pour tous et assez tôt dans la scolarité (Wing, 2006). Depuis, celle-ci a été appliquée à de nombreux domaines tels que les mathématiques et les sciences expérimentales (Weintrop et al., 2016), les arts (Knochel et Patton, 2015) et même l'apprentissage des langues (Sabitzer et al., 2018).
Cet article présente notre travail sur l'acquisition de compétences de base de la PI avec des élèves d'école primaire (8 - 10 ans). Nous nous sommes focalisés sur la capacité des élèves à reconnaître des motifs répétitifs et à les exprimer sous forme de répétitions. Cette abstraction et cette expression ouvrent la voie à un traitement systématique des données.
Nous présentons dans cet article les résultats de l'expérimentation menée en 2018. Celle-ci a impliqué 20 classes venant de 16 écoles pour un total de 447 élèves. Nous avons fait passer aux élèves des questionnaires avant et après l'activité pour mesurer leur capacité à identifier et à coder les répétitions. Nous avons également collecté les traces d'activité de programmation sur l’exerciseur en ligne.
Dans la suite, nous passons en revue l'état de l'art concernant la PI, comment elle est introduite à l'école et comment est réalisée l'évaluation des compétences associées. La section 3 présente la séquence pédagogique que nous avons définie et le contexte expérimental. Nous discuterons l'analyse des résultats dans la section 4 avant de conclure.
2. État de l’art
2.1. La pensée informatique
Il n’existe pas de définition unanimement acceptée du terme pensée informatique. Celle-ci se réfère à un certain nombre d’habilités (abstraction, réflexion algorithmique...) qui ouvrent la voie à un traitement automatisé. On pourra se référer à ce sujet au compte-rendu de la table ronde qui a eu lieu au colloque Didapro 7 (Drot-Delange et al., 2019). Les premiers concepts de PI datent des travaux de Seymour Papert avec le langage Logo (Papert, 1972). Plus récemment, l'article de Jeannette Wing présentant la PI comme une compétence de base au même titre que la lecture, l'écriture et l'arithmétique a déclenché un vif intérêt au sein des communautés éducatives et de recherche (Wing, 2006). Wing insiste notamment sur le fait que la PI ne se réduit pas à la programmation mais correspond plutôt à la capacité de manipuler des abstractions et de résoudre les problèmes qui peuvent être appliqués à différents domaines. Elle prône l'apprentissage de ces compétences dès l'école.
Depuis, un nombre croissant de travaux de recherche se sont développés pour explorer les moyens d'introduire la PI à l'école. Quels sont les concepts fondamentaux à enseigner ? Quelles technologies se prêtent le mieux à ces apprentissages ? etc. Ces questions sont d'autant plus importantes que de nombreux pays ont commencé à introduire la PI et plus généralement « le code » dans les programmes à différents niveaux scolaires.
Rich et al. ont défini des Trajectoires d'Apprentissage en se basant sur une étude de la littérature. Une Trajectoire d’Apprentissage définit les concepts qui peuvent être abordés en fonction de la classe et avec quel niveau de détails (Rich et al., 2017). Elle est formalisée par un ensemble d'objectifs d'apprentissage associés à un chemin d'apprentissage permettant la réalisation de ces objectifs ainsi qu’à des exemples d'activités qui peuvent être mises en œuvre. Les auteurs relèvent que la plupart des travaux sont relatifs à un seul objectif d'apprentissage ou que, quand il y en a plusieurs, ils sont indépendants. Ils observent également que ces objectifs ont pu être appliqués à différents niveaux dans la mesure où ils s'adressent en général à des novices. Pour cette raison, ils se sont inspirés des approches pédagogiques et des programmes de mathématiques pour définir l'ordre d'introduction des concepts de la PI (chemin d'apprentissage). L'article illustre leur approche sur les concepts de Séquence, Répétition et Conditionnelle.
Ching, Hsu et Baldwin ont réalisé une étude des technologies disponibles pour l'enseignement de la PI (Ching et al., 2018). Ils ont identifié les robots pédagogiques, les kits robotiques, les jeux de plateau, les applications en réalité augmentée, les applications ou sites Web pour la programmation (graphique ou textuelle), les outils de développement orientés animation ou jeu. Ces différentes catégories se distinguent selon qu'elles utilisent une manipulation physique ou une interaction sur l'écran et selon que la rétroaction est concrète (par ex., mouvement d'un robot) ou abstraite (c.-à-d. retour sur l'écran). Les résultats de cette étude montrent que les concepts abordés avec ces technologies vont des séquences et répétitions à des concepts plus avancés et peuvent aussi impliquer des activités créatives ou de résolution de problèmes.
Gouws, Bradshaw et Wentworth proposent un cadre de description des compétences liées à la PI (Gouws et al., 2013). En se basant sur une revue de la littérature, ils définissent un ensemble de compétences qui peuvent être abordées à travers la programmation : Processus et Transformations, Modèles et Abstractions, Motifs et Algorithmes, Outils et Ressources, Inférence et Logique, Évaluations et Améliorations. Ils combinent ces compétences avec des niveaux de maîtrise inspirés de la taxonomie de Bloom : Reconnaître, Comprendre, Appliquer et Assimiler. Ce cadre vise à être utilisé pour l'analyse et pour la conception d'activités.
Weintrop et al. s'intéressent à l'introduction des pratiques de la PI en mathématiques et en sciences de manière à permettre une définition des activités de PI indépendante de l'informatique (Weintrop et al., 2016). Les auteurs définissent une taxonomie de 22 pratiques groupées selon les catégories suivantes : Données et Informations, Modélisation et Simulation, Calcul, Résolution de problèmes et Approche Systémique.
Nos travaux s’inscrivent dans les compétences associées aux motifs et algorithmes élaborées par Gouws et al. qui associent reconnaissance des similarités ou motifs et leur traitement algorithmique (la répétition étant un des concepts mobilisables). Nous avons également une approche similaire à Rich et al. qui cherchent dans leurs trajectoires d’apprentissage à introduire les concepts par des exemples hors informatique et/ou par des activités débranchées. Ces auteurs ont notamment travaillé sur la répétition. Un des objectifs d’apprentissage relevés est de reconnaître la nécessité d’une structure répétitive avant même d’aborder la notion de répétition en programmation. Notre approche rentre dans la catégorie des jeux de plateau (déplacement d’un personnage sur une grille en débranché et en numérique) pour amener les élèves à coder un déplacement répétitif. Nous avons choisi d’utiliser une plate-forme plutôt que des robots tangibles, ce qui nous permet de nous abstraire des problèmes matériels (disponibilité et mise à disposition des robots, comportement physique...) et de faciliter les expérimentations à large échelle.
Hormis les travaux qui visent à définir une typologie de compétences ou des concepts de la PI et de leur articulation, on trouve un certain nombre de travaux plus focalisés sur les activités à mettre en œuvre.
Baratè, Ludovico et Malchiodi abordent les notions d'algorithmique et de représentation de l'information en primaire à travers des activités visant à représenter des musiques par l'intermédiaire de briques Lego (Baratè et al., 2017).
Brackmann et al. ont trouvé un effet significatif d'activités débranchées sur les compétences liées à la PI (Brackmann et al., 2017). Ils concluent que ce type d'activité constitue une bonne introduction à la PI mais que des activités « en ligne » sont nécessaires pour aller plus loin.
Aggarwal, Gardner-McCune et Touretzky, quant à eux, ont comparé l'effet des modalités tangible et numérique sur l'acquisition des compétences (Aggarwal et al., 2017). Ils concluent que si la modalité tangible facilite l'appropriation de la syntaxe, la modalité numérique permet de mieux développer la capacité à visualiser et à prévoir l'effet de la séquence d’instructions. Ils suggèrent donc une utilisation limitée de la modalité tangible comme introduction avant de passer au numérique.
Dans le cadre de notre travail, nous nous sommes concentrés sur la détection et la synthèse de motifs répétitifs qui est une des composantes de la capacité d’abstraction propre à la pensée informatique. Cette compétence est abordée à travers des activités tangibles qui permettent d’élaborer cette notion de motif et d’introduire son traitement par la répétition. Les activités numériques permettent de renforcer ces concepts et de les associer à la structure de répétition utilisée en programmation visuelle puis textuelle.
2.2. Évaluation des compétences de la pensée informatique
Outre les questions de l’introduction des concepts de la pensée informatique et des modalités utilisables, il existe un enjeu autour de l’évaluation des compétences acquises, que ce soit dans le cadre de recherches ou en situation d’enseignement.
Brennan et Resnick articulent la PI autour de trois dimensions : Les concepts algorithmiques (boucles, parallélisme, etc.), les pratiques (développement itératif, débugage, etc.) et les perspectives (expression personnelle, connexion avec les autres, etc.) (Brennan et Resnick, 2012). Ils proposent d'évaluer ces dimensions à travers l'analyse des productions, des entretiens basés sur les productions et des projets de développement.
Le rapport du Standford Research Institute (SRI) produit par Snow et al. s'intéresse aux moyens d'évaluer les compétences de la PI (résolution de problème, abstraction, etc.) dans le contexte de l'enseignement Exploring Computer Science (ECS) qui se déroule sur un an au lycée aux États-Unis (Snow et al., 2017). À cette fin, ils proposent des patrons de conception pour la création d'évaluations pertinentes des connaissances et des pratiques. Le rapport couvre l'évaluation des unités suivantes du cours : interaction homme-machine, résolution de problème, conception web et introduction à la programmation. Ces évaluations incluent des quiz, des problèmes, de la lecture de code et le traçage de son exécution.
Grover, Cooper et Pea combinent évaluation formative et sommative dans le cadre d'un module d'introduction des concepts de la PI d'une durée de 6 semaines dans le secondaire (Grover et al., 2014). Les évaluations reposent sur des questionnaires à choix multiples dont la plupart comprennent des extraits de code en Scratch. Certains exercices impliquent de remettre en ordre des blocs de code ou des activités de traçage et de debugage de code.
Seiter et Foreman proposent un cadre pour l'évaluation des compétences de la PI à l'école primaire baptisé Progression of Early Computational Thinking (PECT) (Seiter et Foreman, 2013). Ce cadre s'appuie sur l'évaluation de programmes en Scratch (utilisation d'instructions spécifiques) dans le cadre de patrons de conceptions classiques liés au développement d'animations ou de jeux (par ex., animation, gestion des collisions, etc.). Ces patrons sont mis en relation avec des concepts de la PI. Le cadre proposé a été évalué sur la base des programmes disponibles sur le site Web de Scratch.
Les approches basées sur l'étude du code produit par les apprenants sont intéressantes à titre exploratoire mais chronophages. L'autre mode d'évaluation majoritaire utilise des QCM éventuellement basés sur de la lecture de code. Dans le cadre de cette étude, nous avons élaboré des questionnaires amont et aval spécifiques destinés à évaluer la capacité de reconnaissance et de synthèse des motifs dans un contexte hors programmation (plutôt sur le plan cognitif). L’analyse des traces d’activité sur la plate-forme nous donne par ailleurs des indications sur l’opérationnalisation des concepts algorithmique associés.
3. Cadre expérimental
3.1. Participants et organisation
L'expérimentation de 2018 a impliqué des élèves de CM1/CM2 de 16 écoles de Villeneuve d’Ascq. Vingt classes ont participé pour un total de 447 élèves. L'âge des élèves était compris entre 8 et 10 ans avec un équilibre des genres (49% de filles). L'expérimentation s'est déroulée sur une semaine avec 5 classes par jour (hors mercredi). Les classes sont venues à l'université pour la journée, sous forme de sortie scolaire.
Afin de prendre en charge un aussi grand nombre d'élèves, nous faisons appel aux étudiants de deuxième année de DUT informatique, eux-mêmes encadrés par des enseignants du département informatique. La séquence pédagogique et les activités sont présentées au préalable aux étudiants de façon à ce qu'ils puissent encadrer et accompagner les élèves dans leurs apprentissages.
3.2. Progression pédagogique
La progression pédagogique est présentée dans la Figure 1. Celle-ci inclut des activités débranchées et en ligne liées à l'identification de motifs répétitifs ainsi qu’à leur expression sous forme de séquences d'instructions et de répétitions. Nous avons trois phases décrites dans la suite. Les deux premières durent 1h30 chacune, la dernière dure 2 heures. Les élèves suivent les deux premières phases le matin et la troisième l'après-midi.
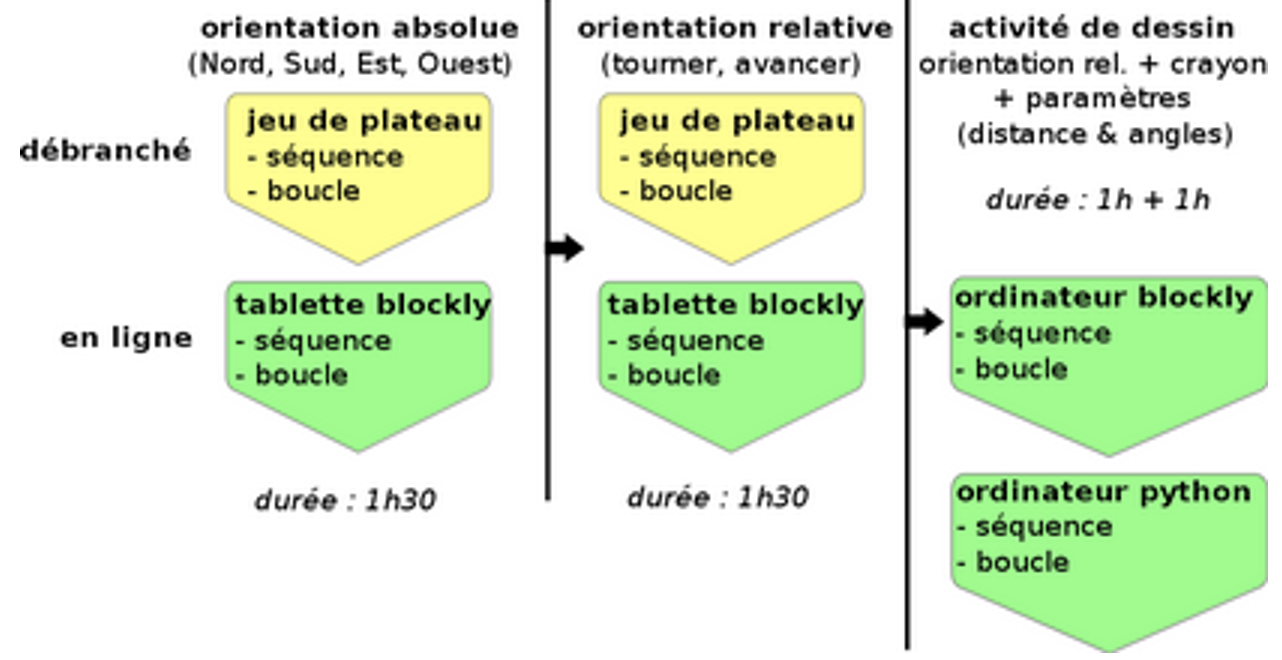
Figure 1 • Progression pédagogique
3.2.1. Personnage avec orientation absolue (phase 1)
Dans cette première phase, les élèves doivent déplacer un personnage sur une grille jusqu'à une case définie en utilisant une orientation absolue (Nord, Sud, Est, Ouest). Ils démarrent l'activité avec un jeu de plateau (cf. figure 2). Les élèves travaillent en groupe de 4 à 6 et prennent à tour de rôle différentes fonctions : élaboreur d’une solution (c.-à-d. algorithme), pointeur d'instruction (qui annonce l'ordre à exécuter), et processeur (qui exécute l'ordre en déplaçant le personnage). La complexité des chemins évolue avec l'ajout d'obstacles et de bonus. Quand la séquence d'ordres gagne en longueur, la frustration des élèves augmente. C'est à ce moment-là que l’on introduit la notion de répétition (répéter n fois).

Figure 2 • Jeu de plateau
Quand les concepts principaux d'instruction, de séquence, de répétition, d'exécution (et de bug) sont compris, les élèves passent sur tablette par binômes pour une activité similaire visant à renforcer les concepts et à permettre un traitement algorithmique via un langage de programmation visuelle basée sur des blocs (Blockly) (cf. figure 3). Pour chaque puzzle, les élèves doivent déplacer un robot jusqu’à la case destination (verte) en récupérant éventuellement des gemmes. Pour cela, les élèves disposent d'un jeu d'instructions spécifique et peuvent être limités en nombre d'instructions. Un puzzle est validé quand le robot arrive sur la case destination et a collecté toutes les gemmes. Les activités évoluent à nouveau de la séquence à la répétition pour renforcer les concepts découverts lors de l’activité débranchée.

Figure 3 • Puzzle sur tablette avec le jeu d’instructions
3.2.2. Personnage avec orientation relative (phase 2)
Cette deuxième phase suit une organisation similaire avec un premier temps sur le jeu de plateau, suivi d’un renforcement sur tablette. Le changement principal tient à l'utilisation d'un personnage orienté qui implique un jeu d'ordres différent (tourner à gauche, tourner à droite, avancer). Cela implique également de se rappeler l'orientation du personnage dans la phase de planification. Le personnage tourne obligatoirement de 90°. Cette phase prépare également à la phase de dessin suivante pour laquelle l'orientation est nécessaire.
3.2.3. Activité de dessin (phase 3)
La dernière phase est réalisée en salle de Travaux Pratiques avec un ordinateur par élève. Les élèves réalisent des activités de dessin avec une tortue (dans l'esprit de Logo). Le jeu d'instructions est similaire à la phase précédente avec en plus la gestion du crayon (lever et baisser pour dessiner) et la paramétrisation des instructions (par ex., avancer(distance) ou tourner à droite(angle)).
Les élèves utilisent la même plate-forme que sur les tablettes. Dans la première partie, ils continuent d'utiliser Blockly pour dessiner. Dans la seconde partie, nous introduisons la programmation Python, les faisant ainsi passer d'une programmation par blocs à une programmation textuelle. Afin de faciliter les choses, les élèves utilisent des instructions en français (par ex., avancer(10)). Toutefois, ils utilisent la syntaxe Python pour les répétitions.
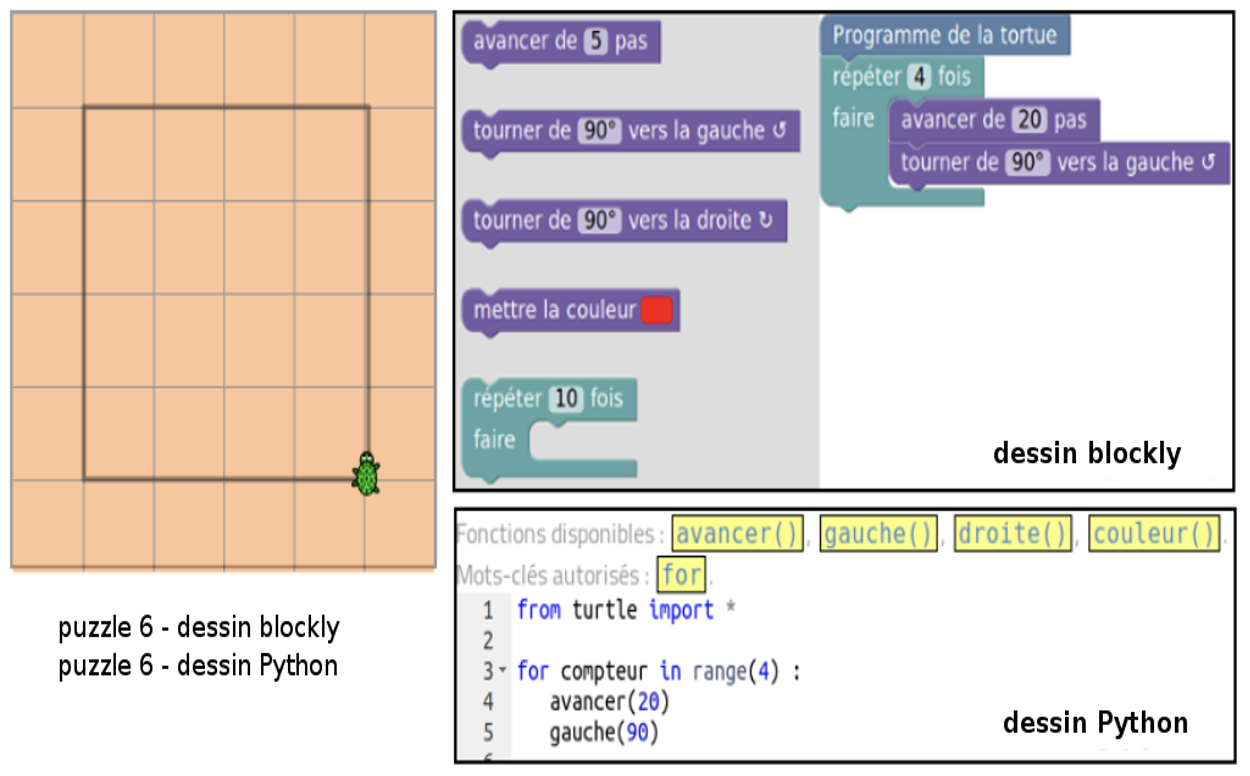
Figure 4 • Passage de la programmation par blocs à la programmation textuelle
Les langages textuels sont en général introduits beaucoup plus tard dans la scolarité. Introduire le langage Python dans la dernière séquence sur un contexte similaire et avec la même interface (cf. figure 4) nous donne des indices sur la capacité des élèves de cette tranche d’âge à transposer leurs compétences de la programmation par blocs à la programmation textuelle.
3.3. Collecte des données
3.3.1. Pré et post tests
Les élèvent passent un test au début et à la fin de la journée de manière à mesurer l'évolution de leur capacité à identifier des motifs répétitifs et à les exprimer sous la forme de répétitions.
Les tests portent sur le codage de motifs avec des lettres. Les élèves sont informés qu'ils peuvent utiliser la notation qui leur semble la plus appropriée, y compris raccourcie. Le pré test consiste à coder une représentation graphique d'une partition de musique où chaque note est représentée par une couleur (cf. figure 5a). Le post test porte sur le codage d'instructions pour la réalisation d'un collier de pâtes (cf. figure 5b). Nous avons choisi deux contextes différents pour éviter que les élèves ne se contentent de se rappeler des motifs du pré test. Cependant, les séquences à analyser sont strictement identiques et présentées exactement dans le même ordre.

Figure 5 • Motifs des pré et post test
Le tableau (cf. tableau 1) présente les motifs utilisés, qui passent d'un corps de boucle ne contenant qu'une instruction et allant jusqu'à trois instructions pour les motifs les plus complexes. La notation présentée ici correspond au pré test mais nous avons exactement les mêmes motifs pour le post test. Le motif correspond à ce qui est présenté aux élèves et l’encodage à ce qui est attendu des élèves, la correspondance définit à quoi correspond le type de motif.
Tableau 1 • Motifs des tests
|
Type |
Correspondance |
Motif |
Encodage |
|
1i |
motif 1 instruction |
RRRRRRRRRRR |
11xR |
|
Nx1i |
N x motifs 1 instruction |
VVRRRBBBB |
2xV 3xR 4xB |
|
2i |
motif 2 instructions |
BRBRBRBRBR |
5x(BR) |
|
3i+2i |
motifs 2 instructions + 1 instruction |
VRRVRRBBBB |
2x(VRR) 4B (2x(V 2R) 4B) |
3.3.2. Activité de programmation
Les activités de programmation ont été réalisées sur une plate-forme de l’association France-IOI. Les quatre séquences pédagogiques comprennent un ensemble de puzzles de difficulté croissante. On retrouve successivement des séquences, des répétitions à une instruction, un mélange des deux, des répétitions à plusieurs instructions, jusqu'aux boucles imbriquées. La première séquence comporte 24 puzzles avec une difficulté très progressive afin que les élèves puissent construire leurs compétences. Les séquences suivantes comprennent de 15 à 18 puzzles. Elles démarrent avec des puzzles simples (séquence), de manière à ce que les élèves puissent transposer leurs compétences sur un nouveau jeu d'instructions, puis la difficulté augmente.
La figure 6 présente quelques puzzles qui sont analysés dans la suite. La plate-forme passe d'un puzzle au suivant après validation mais elle permet également de sélectionner un puzzle spécifique. Chaque séquence réalisée sur la plate-forme dure 30 à 45 minutes suivant les groupes. Cela explique que les élèves n'ont pas réalisé le même nombre de puzzles suivant leur rapidité. Quand de nouveaux concepts sont introduits (par ex., la répétition), le premier puzzle comprend une aide pour la réalisation.
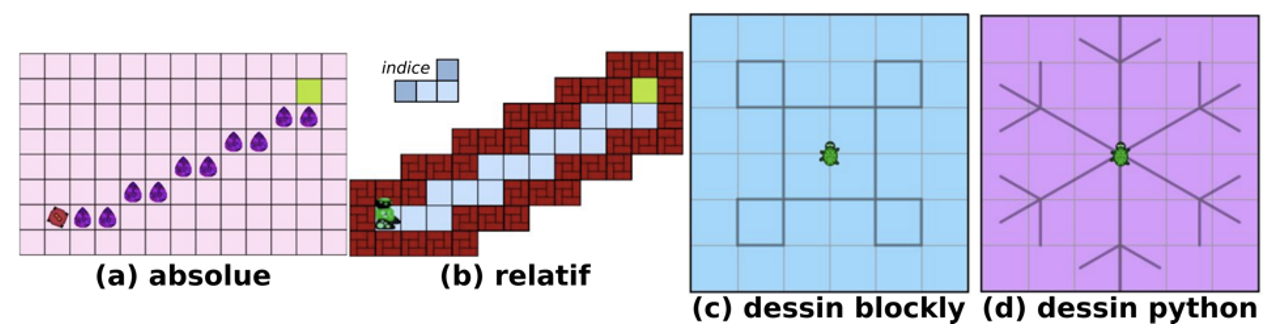
Figure 6 • Puzzles difficiles dans chaque phase
4. Résultats
4.1. Analyses des pré et post tests
Les tests pré et post activité ont été codés en fonction de la reconnaissance ou non des motifs par l'élève, pour arriver à une valeur entre 0 et 1. Pour les 447 élèves, nous obtenons une moyenne m=0,147, écart-type 0,07 pour le pré test et une moyenne m=0,241, écart-type 0,12 pour le post test.
Un t-test apparié nous permet de déterminer si la différence de moyenne est statistiquement significative. Celui-ci nous donne une valeur t(446) = -6,76 (p<0,0001) qui confirme l'impact significatif de la séquence pédagogique sur la capacité des élèves à repérer et à encoder des motifs répétitifs.
Le tableau 2 présente un détail de résultats pour les différents types de motifs de complexité croissante. On note que la reconnaissance des motifs à une instruction et des séquences de répétitions à une instruction augmente de manière significative (+40% pour les deux). Le plus intéressant est probablement que la reconnaissance des motifs plus complexes (2 et 3 instructions) a progressé encore plus. Cela pourrait impliquer qu'après un apprentissage sur des motifs courts, la compétence est généralisée rapidement à des motifs plus complexes par les élèves.
Tableau 2 • Reconnaissance des motifs (nombres d’élèves et pourcentages)
|
|
1i |
Nx1i |
2i |
3i+2i |
|
pré test |
118 (27%) |
102 (23%) |
29 (8%) |
14 (4%) |
|
post test |
166 (38%) |
140 (32%) |
70 (17%) |
56 (14%) |
La figure 5 montre le cas idéal d'un élève qui n'a utilisé aucune notation de répétition dans le pré test mais l'a appliquée avec succès dans le post test.
4.2. Analyses des activités
Nous avons obtenu un export des traces d'activités des participants sur la plate-forme. Celles-ci sont malheureusement limitées car nous n'avons que la dernière validation de l'élève pour chaque puzzle et le moment où cette validation est faite. Nous n'avons donc pas l'historique des essais des élèves. La validation du puzzle peut être positive (c.-à-d. le puzzle est réussi) ou négative.
Pour chaque séquence d'activité en ligne, nous présentons un graphe indiquant pour chaque puzzle le taux de succès (nombre de validations positives / nombre de validations total) et le nombre total de validations (essais). Nous présentons également les transitions entre les niveaux de difficulté (par ex., de séquence à répétition) ce qui nous permet de visualiser les paliers de difficulté.
Pour les deux premières phases, les élèves partagent une tablette à deux et résolvent un puzzle chacun leur tour. En pratique, ils collaborent généralement pour résoudre le puzzle même s'ils n'en ont pas eu la consigne. Ceci explique le nombre d'essais maximal autour de 200. Pour la dernière phase, les élèves travaillent seuls sur ordinateur et nous avons potentiellement 447 essais (nombre d’élèves impliqués). Nous avons perdu des essais sur la première et la dernière séquence suite à des problèmes techniques, ce qui explique des chiffres inférieurs.
4.2.1. Analyse des activités avec orientation absolue (phase 1)
La figure 7 montre les résultats de la première phase. Nous avons une progression mesurée de la difficulté des puzzles donnant un taux de succès supérieur à 90%.
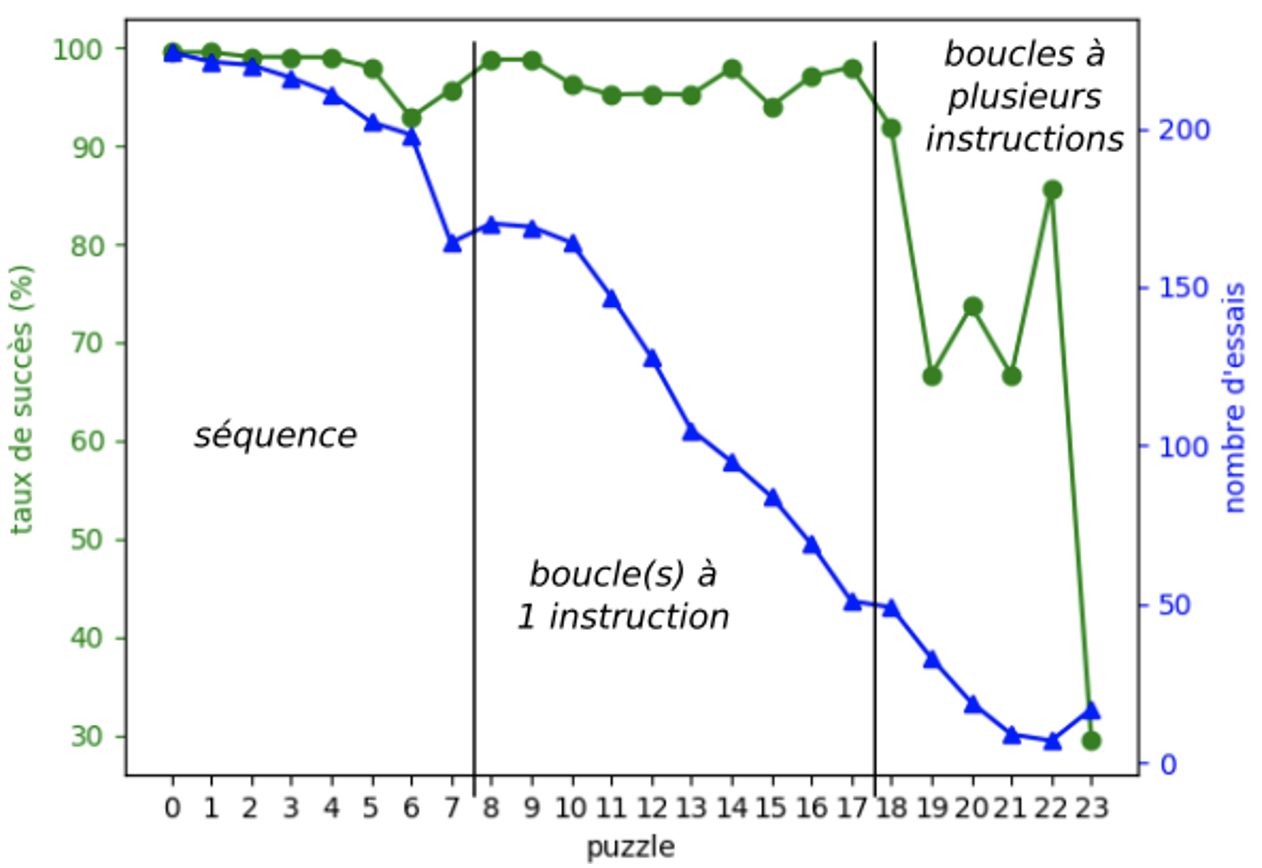
Figure 7 • Résultats de la 1ère phase (orientation absolue)
On observe une diminution du nombre d'essais quand on aborde les puzzles avec répétitions, ce qui indique que certains élèves commencent à rencontrer des difficultés. Toutefois, la chute brutale correspond aux répétitions impliquant plusieurs instructions (c.-à-d. motifs plus longs) avec un taux de succès qui tombe à 66% pour le puzzle 19 (cf. figure 6a) (le puzzle 18 est un tutoriel).
L’étude des programmes produits par les élèves permet d’observer que, dans l’ensemble, le bloc répéter est relativement bien utilisé, dans la mesure où sur la séquence on ne retrouve que trois occurrences de programme où la valeur par défaut pour la répétition a été laissée (10). Quelques élèves ont utilisé une boucle à une répétition. Cela s’est principalement produit dans les premiers puzzles comprenant une séquence d’une instruction et une répétition (puzzle 10 – 16 solutions sur 166, soit 9,6% ; puzzle 11 – 10 solutions sur 150, soit 6,6%). Ce phénomène devient marginal dans les puzzles suivants (moins de 3 par puzzle).
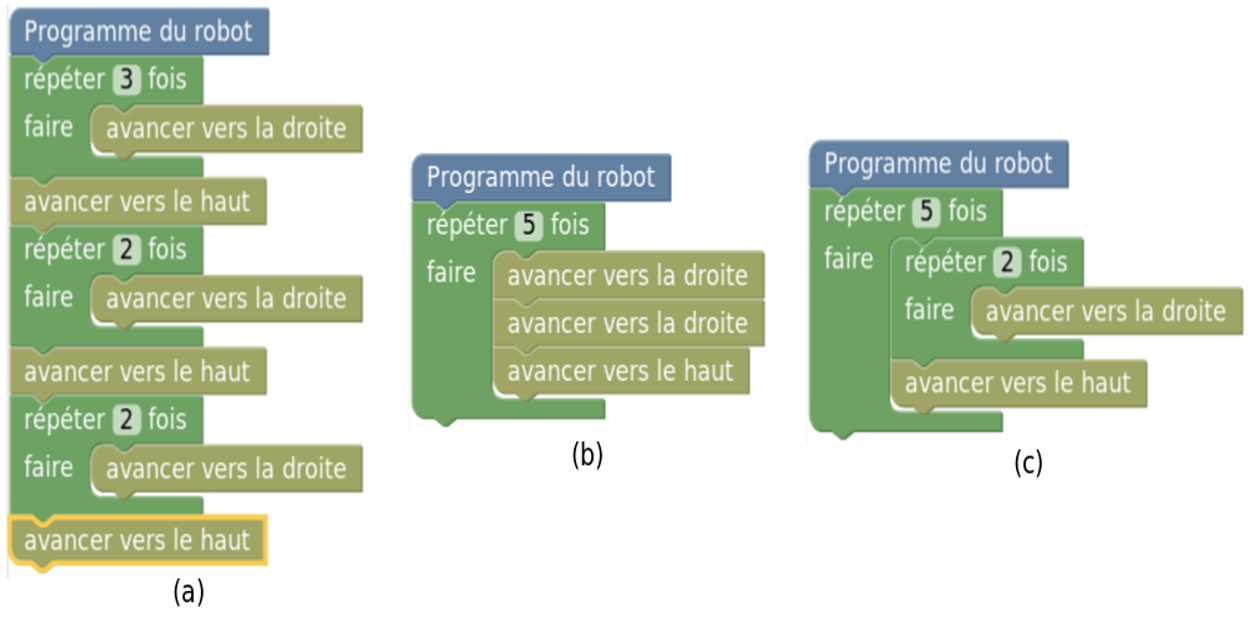
Figure 8 • Orientation absolue : solutions pour le puzzle 19
Si on considère plus précisément le puzzle 19, nous avons 33 solutions soumises dont 22 correctes (66%). Parmi les solutions incorrectes, 4 n’utilisent pas de boucle (12%) et 7 contiennent des boucles mais à une seule instruction (21%), montrant qu’ils n’ont pas détecté le motif de longueur supérieur. La figure 8a montre un exemple de ce type de solution où l’élève a atteint la limite des blocs autorisés. Pour les solutions correctes, on a 19 solutions attendues avec une répétition de motif de longueur 3 (cf. figure 8b) et 3 solutions avec deux boucles imbriquées (cf. figure 8c).
4.2.2. Analyse des activités avec orientation relative (phase 2)
La figure 9 correspond aux résultats de la deuxième phase. Le taux de succès proche de 90% ou supérieur indique que les élèves ont réussi à transférer leurs compétences sur le nouveau langage. On note également une amélioration de leur capacité à gérer les boucles à une instruction. En effet, on observe encore 137 essais avec un succès raisonnable pour le puzzle 7 (à comparer aux 51 essais du puzzle 17 de la phase précédente). À nouveau, passer aux répétitions impliquant plusieurs instructions présente une difficulté majeure. Le puzzle 8 (cf. figure 6b) qui a un nombre d'essais significatif atteint un taux de succès de 56% seulement. Et ce, malgré le fait qu'étant le premier puzzle de ce type, il y avait une indication sur le motif à traiter.
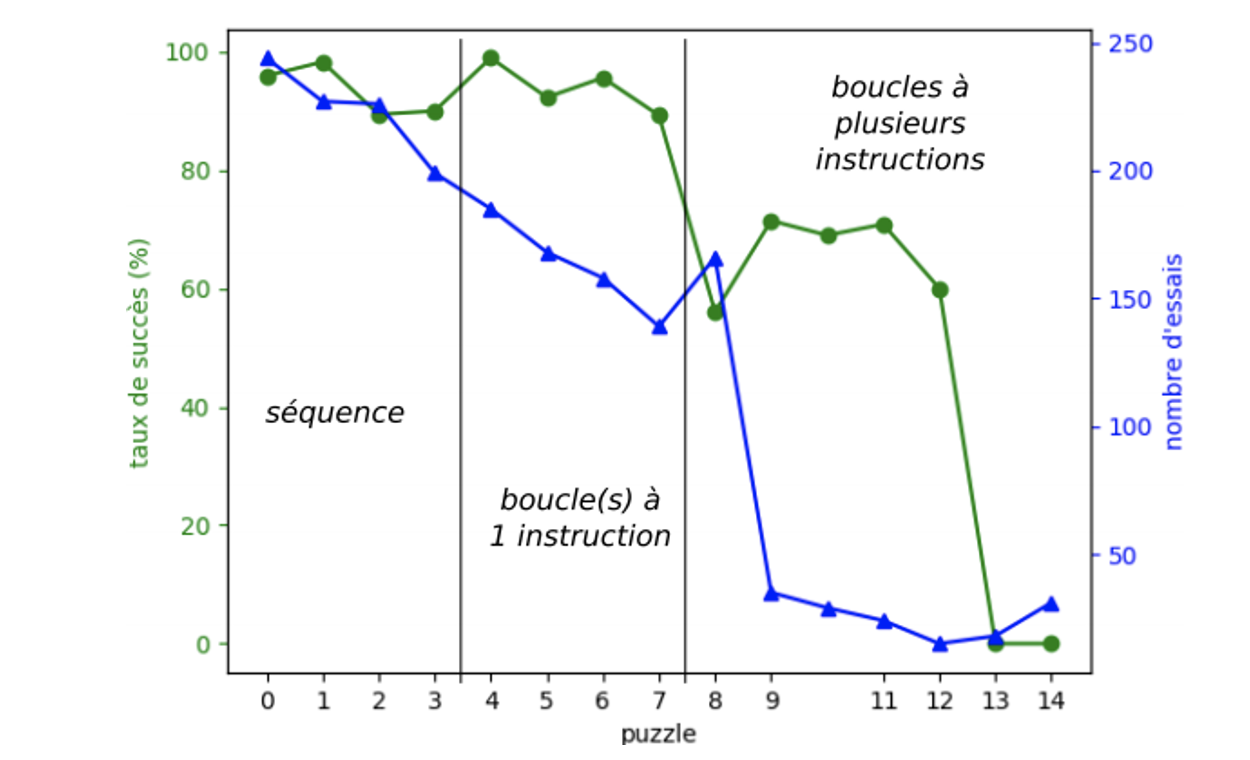
Figure 9 • Résultats de la 2ème phase (orientation relative)
Quand on analyse les programmes produits par les élèves, on ne trouve plus qu’un nombre marginal de répétitions avec une seule itération (3 maximum sur un des puzzles), ce qui confirme la bonne maîtrise du paramétrage du bloc et un bon dénombrement des actions à réaliser.
L’étude des solutions pour le puzzle 8 (cf. figure 6b) montre 27 solutions (incorrectes) sans boucles (15%) pour 148 solutions avec répétitions. Parmi ces dernières, 50 sont fausses (34%). 17 de ces solutions combinent séquences et répétitions à une seule instruction, indiquant la difficulté à passer à un motif de longueur supérieure. Pour les autres, elles révèlent la difficulté à isoler le motif répété (cf. par exemple figure 10a). On retrouve au final 48 solutions conformes à la réponse attendue (27%) (cf. figure 10b).
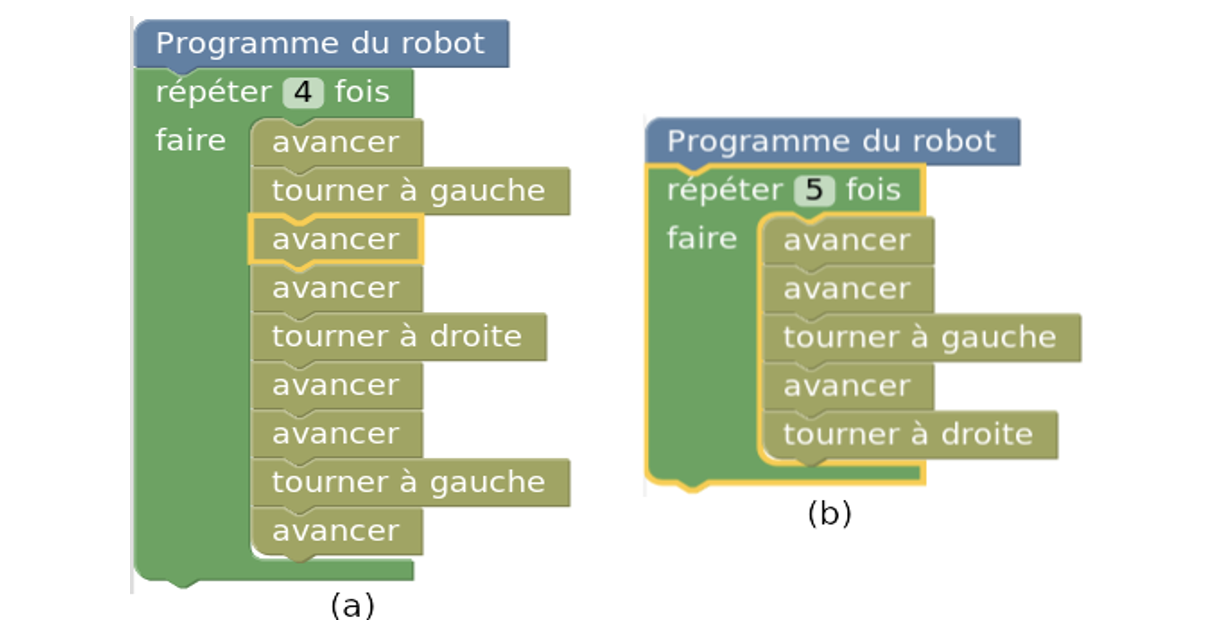
Figure 10 • Phase 2 (orientation relative) : solutions pour le puzzle 8
4.2.3. Analyse des activités de dessin en Blockly (phase 3)
La dernière phase introduit de nouvelles difficultés. D'abord les instructions sont paramétrées. Ensuite, on commence à avoir des angles différents de 90° que les élèves n'ont pas encore vu en classe. À nouveau, le nombre d'essais et le taux de succès des premiers puzzles (y compris avec répétitions) indiquent que le changement de langage n'est pas un problème pour les élèves une fois que les compétences liées aux séquences et répétitions sont intégrées (cf. figure 11). Les puzzles qui combinent séquences d'instructions et répétitions comprenant plusieurs instructions restent difficiles (puzzles 9 à 11, le 9 fournissant des indices) dans la mesure où l'on voit le nombre d'essais chuter. Pour le puzzle 11 (voir figure 6c), nous avons encore 129 essais mais avec un taux de succès de 58%. Peu d'élèves ont abordé les puzzles avec des boucles imbriquées mais avec un taux de succès légèrement supérieur à 60%.
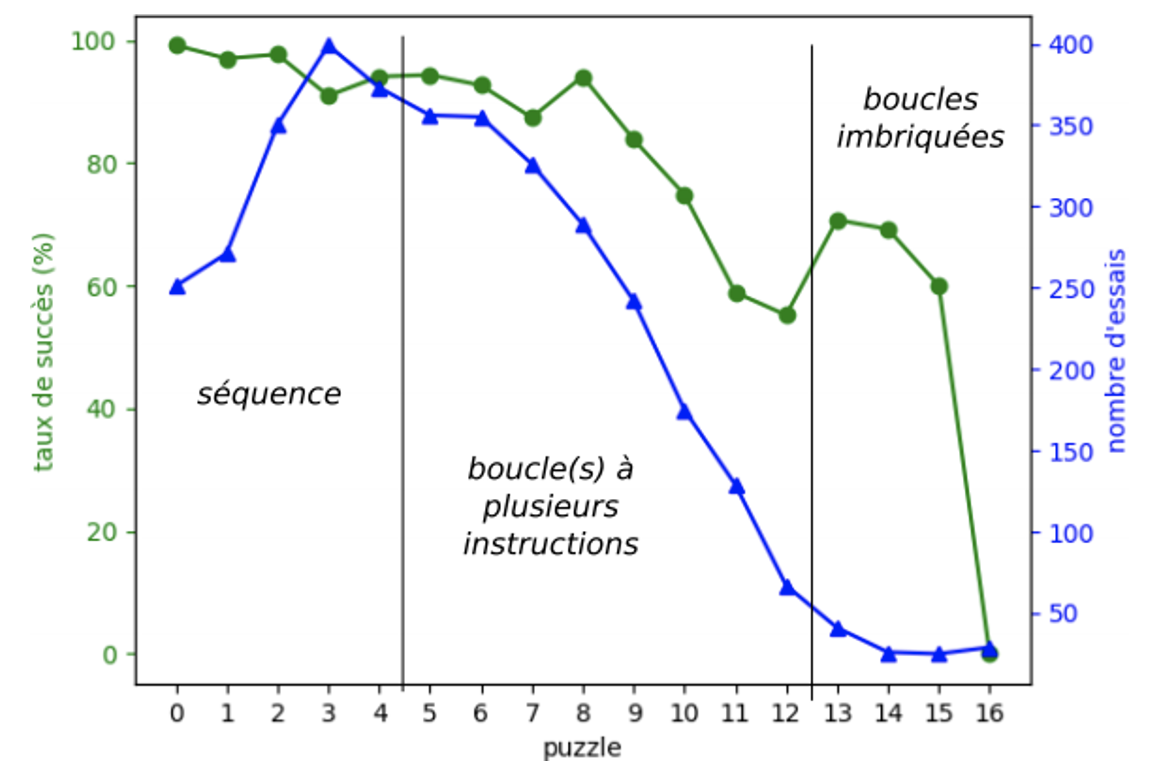
Figure 11 • Résultats de la 3ème phase (dessin en Blockly)
Si on s’intéresse au puzzle 9 (cf. figure 12a), on a 249 essais dont 82 solutions sans boucles (32%) - le nombre de blocs autorisés le permettait. Sur ces 82 solutions, 60 ont été validées correctes (par ex., figure 12b). Une hypothèse pour cette proportion non négligeable de solutions basées sur la séquence est que le puzzle nécessite un angle différent de 90° qui présente une difficulté pour les élèves.
Parmi les 167 solutions avec boucles, 145 ont été validées par la plate-forme (58%). 79 correspondent à la solution attendue (31%) (cf. figure 12d). Parmi les solutions non optimales, on retrouve des solutions du type de la Figure 12c qui témoignent de la difficulté à bien coder le motif répétitif.
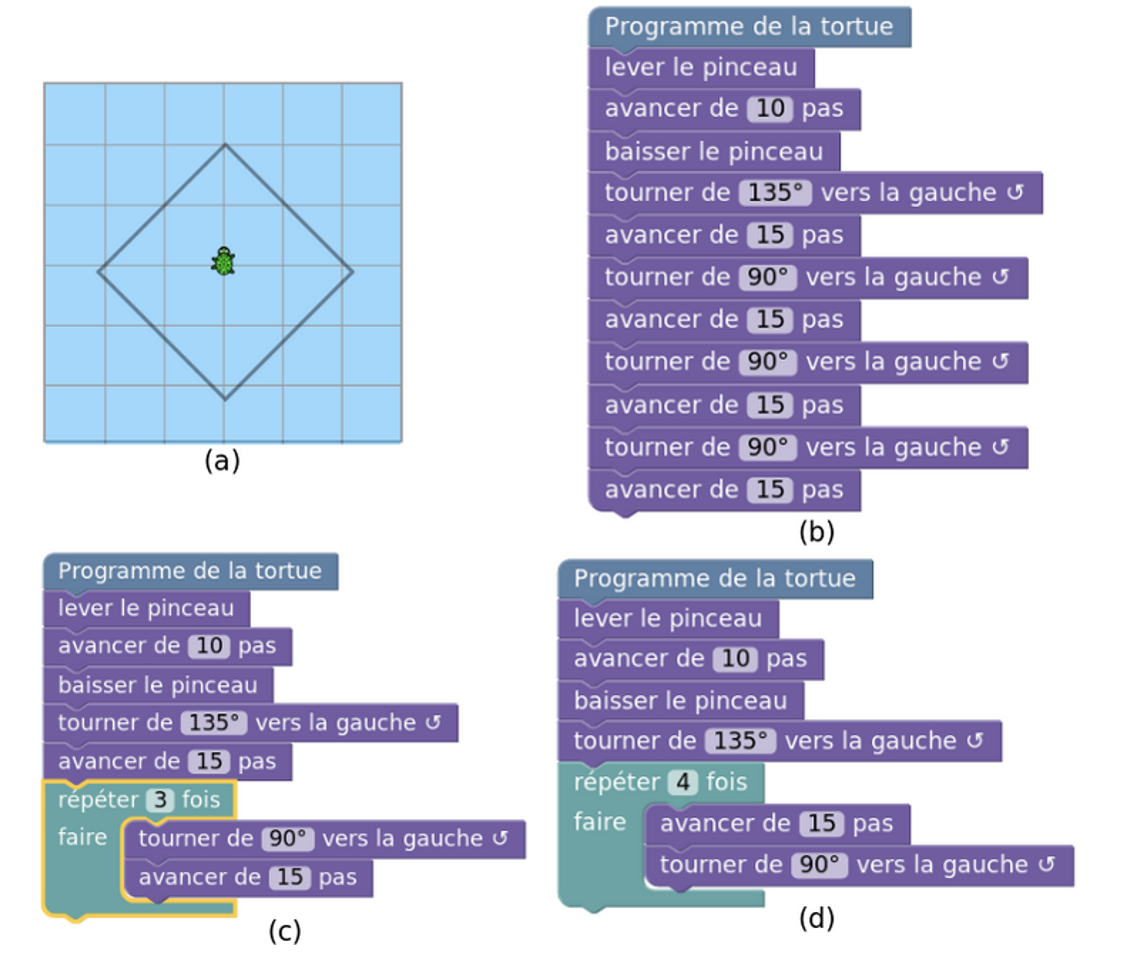
Figure 12 • Phase 3 (dessin en Blockly) : puzzle 9 et solutions trouvées
Le puzzle 11 (cf. figure 6c) quant à lui totalise 129 solutions soumises. On retrouve 25 solutions sans répétition qui sont toutes incorrectes (19%). Ici, la difficulté à trouver le motif a amené une grande diversité de réponses avec 38 solutions différentes. Ces solutions ont été acceptées car la plate-forme valide uniquement le tracé réalisé. Ainsi, on trouve 9 solutions (7%) avec une répétition à 10 itérations (valeur par défaut), probablement parce que les élèves étaient concentrés sur la recherche du motif aux dépens de la réflexion sur le nombre d’itérations nécessaires. On observe également 25 solutions (19%) utilisant une boucle imbriquée (par exemple dans la figure 13a). La solution (cf. figure 13b) basée sur une seule répétition présente le même défaut que la solution précédente (changements de sens inutile). Enfin, la solution présentée en figure 13c représente la solution la plus courante.
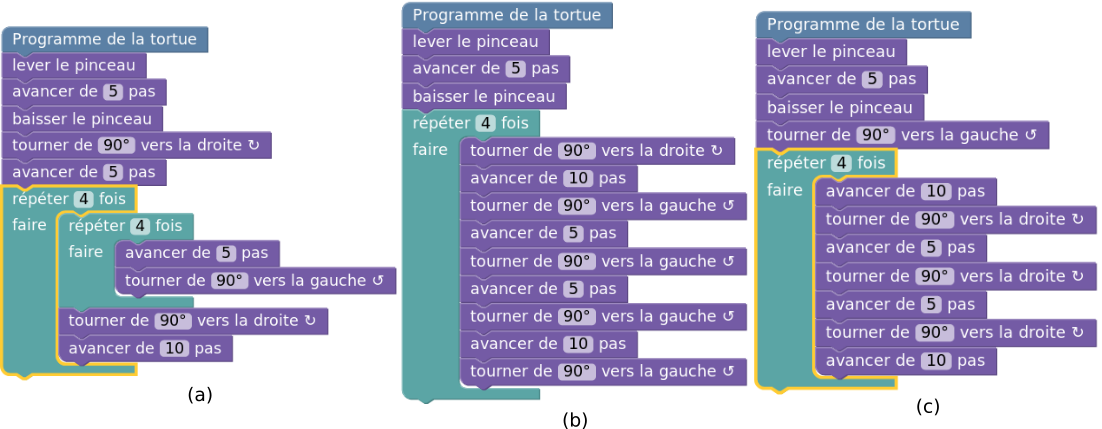
Figure 13 • Phase 3 (dessin en Blockly) : solutions pour le puzzle 11
4.2.4. Analyse des activités de dessin en Python (phase 3)
La figure 4 permet de voir que les élèves peuvent utiliser des boutons pour générer les instructions afin d'éviter d'avoir à tout taper au clavier. Ils doivent malgré tout adapter les paramètres de ces instructions à leurs besoins.
Comme le montre la figure 14, la première séquence de puzzles a toujours un bon taux de succès avec 82% et une bonne participation (nous avons perdu des traces suite à un problème technique). C'est un résultat intéressant qui montre que les élèves ont bien transposé leurs compétences d'un langage visuel à un langage textuel. Les puzzles impliquant séquence et répétition sont toujours difficiles (puzzles 8 et 9) avec un taux de succès à peine supérieur à 50%. Les boucles imbriquées sont également un point difficile. Le puzzle 10 est un tutoriel. Le puzzle 11 présenté en figure 6d atteint seulement 18% de taux de succès avec un faible nombre d'essais. Le dernier puzzle correspond à une activité où les élèves peuvent dessiner librement. Il n'y a donc pas de condition de validation. Le graphe montre qu'un bon nombre d’essais ont été réalisés par les élèves bien qu’on soit sur la modalité textuelle.
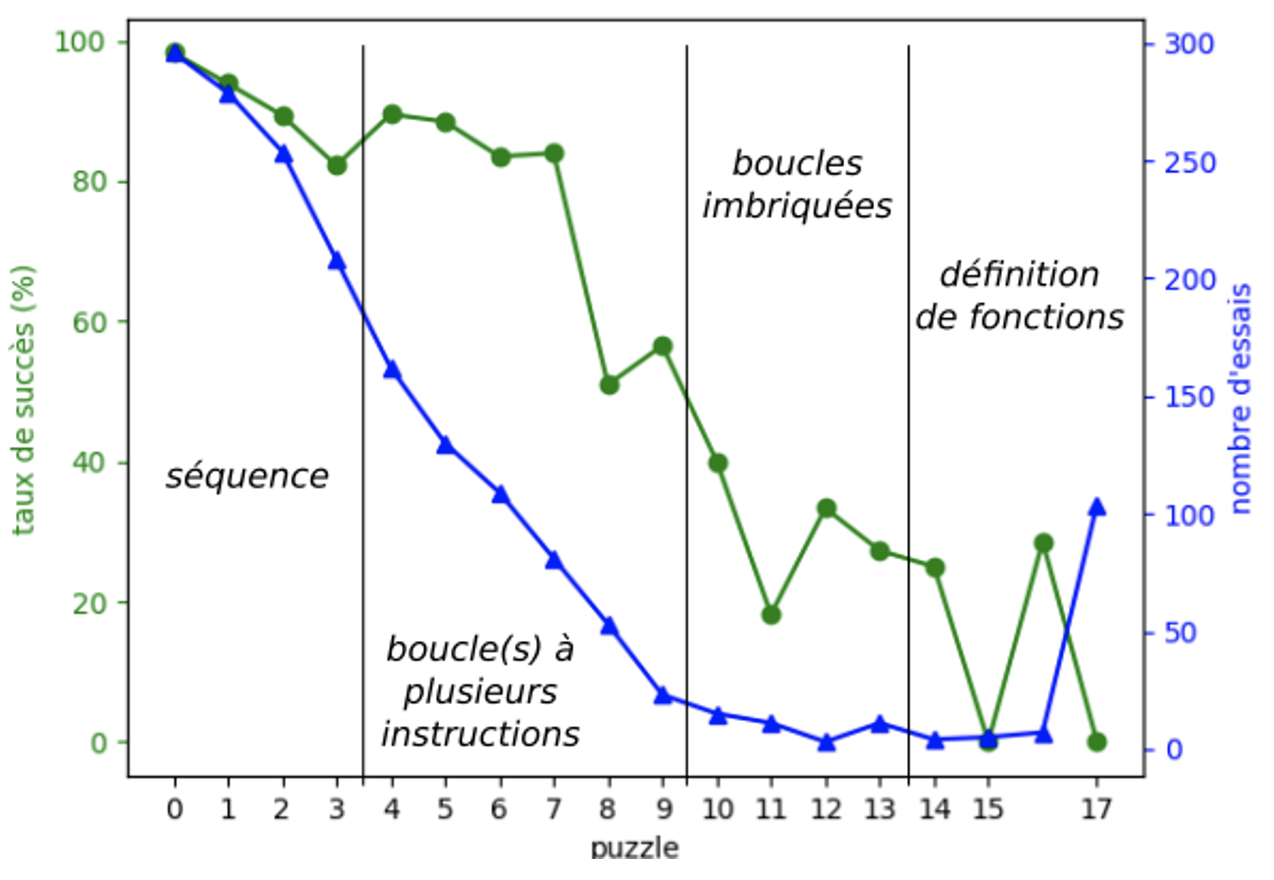
Figure 14 • Résultats de la 3ème phase (dessin en Python)
L’étude des programmes produits montre les difficultés liées à la syntaxe qui apparaissent avec le langage textuel. On retrouve notamment dans les programmes non validés l’oubli du nombre d’itérations dans les répétitions ou des parenthèses enlevées par erreur dans les passages de paramètre.
5. Conclusion
Cet article porte sur l'apprentissage des concepts fondamentaux et des compétences de la PI par des élèves de 8 - 10 ans. Nous avons principalement travaillé sur la notion de motif et de traitement répétitif. Nous considérons en effet que la capacité d’identification de motifs caractéristiques et leur description synthétique constitue l’une des compétences cruciales de la PI. Pour cela, nous avons conçu une séquence pédagogique pour initier les élèves aux notions d’instruction, de séquence et de répétition. Cette séquence leur permet de pratiquer ces compétences avec différents langages (libre, blockly et textuel) et sous différentes modalités (débranchées et en ligne).
Cette séquence a évolué depuis nos premières expérimentations en 2014 et nous avons un nombre croissant de classes impliquées. Nous cherchons également à améliorer nos instruments de mesure pour vérifier l'impact sur les élèves (pré et post tests et analyse des activités).
Les résultats de l'expérimentation de 2018 sont encourageants. L'analyse statistique des tests montre l'impact significatif de la séquence pédagogique et nous avons une augmentation significative des élèves qui identifient les motifs répétitifs et sont capables de les synthétiser sous forme de répétitions. Il semble également qu'une fois que les élèves ont acquis cette compétence pour des motifs de longueur 2 (2 instructions dans le corps de la boucle), ils sont capables de généraliser à des motifs plus longs.
L’analyse des programmes produits montre également une bonne utilisation de la répétition dans la mesure où elle est généralement paramétrée correctement (bonne évaluation du nombre d’itérations nécessaires). La difficulté à appréhender les motifs de longueur supérieure à un se retrouve dans des programmes non optimaux où le motif est partiellement pris en compte. Comme on peut s’y attendre le passage à Python représente une difficulté supplémentaire avec des difficultés liées au respect de la syntaxe du langage.
Les résultats de l'analyse des activités sont à prendre avec précaution dans la mesure où, bien sûr, ils sont aidés par les étudiants voire les professeurs ou des parents. Avec un étudiant pour 4 à 6 élèves, on peut toutefois espérer que cela n'a pas un impact trop fort sur les résultats. Ce type d’activité peut raisonnablement être reproduit en classe sous forme d’ateliers avec des petits groupes d’élèves. Une fois les consignes comprises, les activités débranchées peuvent être réalisées en quasi autonomie (activité collaborative). Les activités numériques, quant à elles, peuvent être réalisées sur tablette ou ordinateur et la plate-forme gère les rétroactions ainsi que l’avancée dans les parcours.
Les élèves reçoivent un diplôme à la fin de la journée qui donne l'adresse de la plate-forme ainsi que leur code d'identification. Nous avons observé environ 300 accès dans les jours suivants et jusqu'à deux mois après (date de la récupération des données). Toutes les séquences ont été utilisées y compris le dessin en Python pour laquelle il y a eu 271 essais. Ces éléments sont encourageants et montrent la motivation des élèves.
 À
propos des auteurs
À
propos des auteurs
Marielle Léonard est ingénieur
d’étude pour le laboratoire CRIStAL, université de Lille.
Parallèlement, elle prépare une thèse en sciences de
l’éducation au laboratoire CIREL, université de Lille. Le
sujet de cette thèse porte sur une approche didactique et instrumentale
des fondamentaux de l’algorithmique.
Après avoir enseigné 13 ans comme professeur des écoles
dans le premier degré, elle obtient un master en Ingénierie
Médiation e-Éducation en 2020. Depuis 2015, elle contribue
à la conception de ressources pour l’initiation à la
programmation informatique et aux sciences du numérique sur les
plateformes de l’association France-ioi.
Adresse : Université de Lille,
CNRS, Centrale Lille, UMR 9189 CRIStAL, F-59000 Lille, France
& CIREL, Centre Interuniversitaire de Recherche en Éducation de
Lille, EA 4354, F-59000 Lille, France
Courriel : marielle.leonard@univ-lille.fr
Yann Secq est enseignant-chercheur en Informatique à l’Université de Lille au sein de l’équipe NOCE de CRIStAL. Ses recherches portaient initialement sur la modélisation et le génie logiciel des systèmes multi-agents particulièrement dans le cadre de simulations orientée individus à large échelle. Ensuite, il s’est orienté vers la didactique de l’informatique. Ses préoccupations en recherche et en enseignement portent maintenant sur la diffusion à large échelle de la pensée informatique en contexte scolaire principalement et dans le cadre de la formation initiale et continue des enseignants d’écoles élémentaires ou d’établissements secondaires.
Adresse : Université de Lille, CNRS, Centrale Lille, UMR 9189 CRIStAL, F-59000 Lille, France
Courriel : yann.secq@univ-lille.fr
Yvan Peter est enseignant-chercheur en Informatique à l’Université de Lille au sein de l’équipe NOCE de CRIStAL. Ses recherches se situent dans le domaine des Interactions Homme-Machine (IHM) et des Environnements Informatiques pour l’Apprentissage Humain (EIAH). Il s’intéresse plus particulièrement aux plates-formes permettant de supporter les activités d’apprentissage : orchestration des scénarios pédagogiques, apprentissage mobile... et plus récemment l’apprentissage de l’informatique.
Adresse : Université de Lille, CNRS, Centrale Lille, UMR 9189 CRIStAL, F-59000 Lille, France
Courriel : Yvan.Peter@univ-lille.fr
REMERCIEMENTS
Nous remercions l'association France-IOI pour la mise à disposition de la plate-forme. Ce travail est partiellement soutenu par les projets Interreg Dig-e-Lab (https://dig-e-lab.eu) et Teach Transition (https://teachtransition.eu).
RÉFÉRENCES
Aggarwal, A., Gardner-McCune, C. et Touretzky, D. S. (2017). Evaluating the effect of using physical manipulatives to foster computational thinking in elementary school. Dans Proceedings of the 2017 ACM SIGCSE Technical Symposium on Computer Science Education - SIGCSE’17, 9-14. Disponible sur internet.
Baratè, A., Ludovico, L. A. et Malchiodi, D. (2017). Fostering computational thinking in primary school through a LEGO®-based music notation. Procedia Computer Science, 112, 1334-1344. Disponible sur internet.
Brackmann, C. P., Román-González, M., Robles, G., Moreno-León, J., Casali, A. et Barone, D. (2017). Development of computational thinking skills through unplugged activities in primary school. Dans Proceedings of the 12th Workshop on Primary and Secondary Computing Education - WiPSCE’17, 65-72. Disponible sur internet.
Brennan, K. et Resnick, M. (2012). New frameworks for studying and assessing the development of computational thinking. Communication présentée à annual American Educational Research Association meeting (AERA 2012), Vancouver, BC, Canada. Disponible sur internet.
Ching, Y.-H., Hsu, Y.-C. et Baldwin, S. (2018). Developing computational thinking with educational technologies for young learners. TechTrends, 62(6), 563-573. Disponible sur internet.
Drot-Delange, B., Pellet, J. P., Delmas-Rigoutsos, Y. et Bruillard, É. (2019). Pensée informatique : points de vue contrastés. Sciences et Technologies de l'Information et de la Communication pour l'Éducation et la Formation, 26(1), 39-61.
Gouws, L., Bradshaw, K. et Wentworth, P. (2013). Computational thinking in educational activities. Dans Proceedings of the 18th ACM conference on Innovation and technology in computer science education (ITiCSE’13), 10-15.
Grover, S., Cooper, S. et Pea, R. (2014). Assessing computational learning in K-12. Dans Proceedings of the 2014 conference on Innovation and technology in computer science education (ITiCSE ’14), 57-62. Disponible sur internet.
Knochel, A. D. et Patton, R. M. (2015). If Art Education Then Critical Digital Making: Computational thinking and creative code. Studies in Art Education, 57(1), 21-38. Disponible sur internet.
Papert, S. (1972). Teaching children thinking. Programmed Learning and Educational Technology, 9(5), 245-255. Disponible sur internet.
Rich, K. M., Strickland, C., Binkowski, T. A., Moran, C. et Franklin, D. (2017). K-8 learning trajectories derived from research literature: Sequence, repetition, conditionals. Dans Proceedings of the 2017 ACM Conference on International Computing Education Research (p. 182-190). Disponible sur internet.
Sabitzer, B., Demarle-Meusel, H. et Jarnig, M. (2018). Computational thinking through modeling in language lessons. Dans Proceedings of the 2018 IEEE Global Engineering Education Conference (EDUCON) (p. 1913-1919). Disponible sur internet.
Seiter, L. et Foreman, B. (2013). Modeling the learning progressions of computational thinking of primary grade students. Dans Proceedings of the Ninth Annual International ACM Conference on International Computing Education Research (p. 59-66). Disponible sur internet.
Snow, E., Tate, C., Rutstein, D. et Bienkowski, M. (2017). Assessment design patterns for computational thinking practices in exploring computer science. Menlo Park, CA : SRI International. Disponible sur internet.
Weintrop, D., Beheshti, E., Horn, M., Orton, K., Jona, K., Trouille, L. et Wilensky, U. (2016). Defining computational thinking for mathematics and science classrooms. Journal of Science Education and Technology, 25(1), 127-147. Disponible sur internet.
Wing, J. M. (2006). Computational Thinking. Communications of the ACM, 49(3), 33-35. Disponible sur internet.
Yvan PETER, Yann SECQ, Marielle LÉONARD, Reconnaissance de motifs redondants et répétitions : introduction à la Pensée Informatique, Revue STICEF, Volume 27, numéro 2, 2020, DOI:10.23709/sticef.27.2.3, ISSN : 1764-7223, mis en ligne le 24/05/2021, http://sticef.org
© Revue Sciences et Technologies de l´Information et de la Communication pour l´Éducation et la Formation, 2020